流形距离与压缩感知核稀疏投影的局部线性嵌入算法*
马 丽 董唯光 安志龙
(1.陕西铁路工程职业技术学院电气与信息工程系 渭南 714000)
(2.兰州交通大学自动化与电气工程系 兰州 730070)(3.陕西铁路工程职业技术学院管理工程系 渭南 714000)
1 引言
随着5G 信息技术的不断发展与更新,人类收集和处理高维度数据的能力越来越强。而通过海量数据如何实现重要价值的提取,是数据处理研究的主要瓶颈。因此,数据降维尤为重要。数据降维,一方面可以解决“维数灾难,降低数据复杂度;另一方面可以更好地学习数据中的信息。
作为信息科学领域研究热点之一,流形学习,主要用于数据维数约简。流形学习是从高维采样数据中恢复低维流形本质结构,即找到高维空间中的低维流形并求出相应的嵌入映射,实现维数约简或数据可视化。经典的非线性流形学习算法有等距特征映射算法(Isometric map,Isomap)[1]、局部线性嵌入算法(Locally Linear Embedding,LLE)[2]、Laplacian 特征映射算法(Laplacian Eigenmaps,LE)[3]、Hessian 特征映射算法(Hessian-based Locally Linear Embedding,HLLE)[4]和局部切空间排列算法(Local Tangent Space Alignment,LTSA)[5]等。
针对局部降维算法中近邻参数K 的选取问题,很多研究者提出了自适应选择近邻算法[9~12]。但这些算法计算复杂度在处理非均匀分布的数据流形时,欧氏距离作为相似性度量无法反映样本的全局一致性,而流形距离[15]能有效反映样本固有的全局一致性信息。故本文提出一种基于流形距离的邻域选择算法,通过流形距离作为样本间相似性度量的测度,对空间分布复杂的流形结构的数据具有更好的性能。
受到压缩感知(Compressive Sensing,CS)理论[16~18]的启发,提出基于压缩感知理论的核稀疏表示投影(Kernel Sparse Representation Projections based on Compressive Sensing,CS-KSRP)。该思想首先将数据映射到更高维的特征空间,然后利用压缩感知理论在高维特征空间中进行核函数的稀疏表示。因为噪声不具有稀疏性[20],在局部线性嵌入算法中引入该稀疏投影[19,21],可以实现对原始数据的降噪过程。将上述两种思想相结合,提出了流形距离与压缩感知核稀疏投影相结合的局部线性嵌入算法。从实验数据集的降维效果可以得出本文所提出的算法能有效避免对邻域参数的敏感并能达到降噪的目的。
2 局部线性嵌入算法
局部线性嵌入算法(LLE)[2]主要是通过在低维嵌入空间中保持每个数据点的近邻重构系数来保持整个数据的流形结构,即以重构权值矩阵作为高维观测空间与低维嵌入空间的联系桥梁。由于流形上的局部可以认为是一个局部欧式空间,因此每个样本点与其近邻样本之间是线性关系,可以用其近邻样本的线性组合来重构。
LLE算法包含以下三个基本步骤:
1)构造近邻域:在高维数据空间对于给定的数据集X=[x1,x2,…,xn]∈RD×n,通过欧氏距离寻找与每个样本点最近的k个近邻,xi的k个近邻集合为N(xi)={xi1,xi2,…,xik}。
2)计算高维空间中的局部线性表示:权值矩阵W对于每个样本点xi及其近邻集N(xi)={xi1,xi2,…,xik}。权值矩阵W是通过最小二乘法极小化每个样本点的重构误差得到,即:
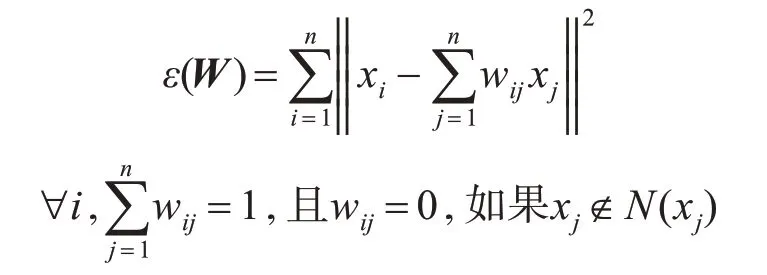
其中权值wij反映了样本点xj对xi重构的贡献。
3)求低维嵌入Y:在低维空间用各个样本点的近邻重构其本身,即求Y=[y1,y2,…,yN],使得重构误差最小,设置误差函数为
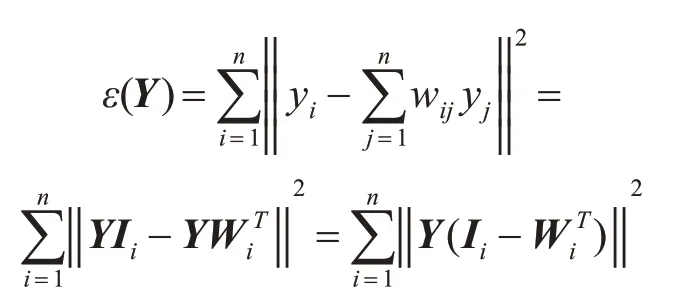
E=(I-W)T(I-W) ,最终求得。
为实现选择最近邻点的准确选择,图1 中(b),(c),(d)为用LLE 算法对实验数据集 Swiss-roll 进行K近邻算法构建邻域图,最近邻点数k=8,10,12,所得到的二维嵌入结果。从图中看到随着k 值的变化,会有不同的低维嵌入图形,说明LLE 算法对邻域参数的选择比较敏感。故本文提出了一种基于流形距离度量相似性的近邻选择算法,根据流形距离计算样本间的相似性,较好地解决了LLE算法的邻域选择问题。
3 基于流形距离的邻域选取
3.1 流形距离
由于用欧氏距离来选择最近邻域时,选择的近邻点不能准确地表征流形上的真正邻域结构。为实现数据最近邻点的选择,提出一种新的相似度度量来计算数据点间的最短距离。
定义1.流形上两点xi,xj的线段长度定义为
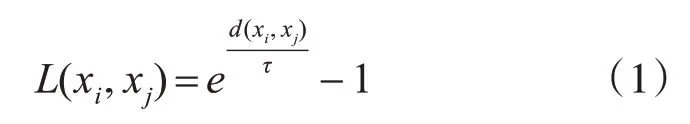
d(xi,xj)表示xi,xj之间的欧氏距离,τ是可调参数。
定义2.将数据点看作是图G=(V,E)的顶点,令p∈Vl,表示图上的一个长度为l=|p|-1的连接点p1与的路径,其中边 (pk,pk+1),1 ≤k<|p|。令Pij表示连接数据点xi,xj的所有路径的集合,则xi与xj之间的流形距离如下:
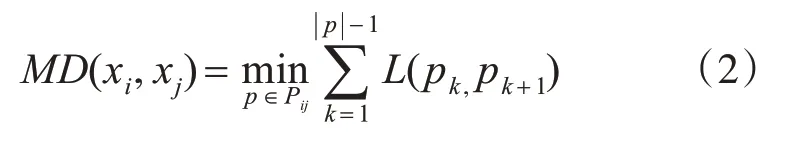
其中,L(a,b)表示两点间流形上的线段长度。流形距离满足以下四个条件:
1)对称性:MD(xi,xj)=MD(xj,xi);
2)非负性:MD(xi,xj)≥0 ;
3)三角不等式:对任意的xi,xj,xk,有MD(xi,xj)≤MD(xi,xk)+MD(xk,xj);
4)自反性:MD(xi,xj)=0 ,当且仅当xi=xj。
数据点间相似度可以用距离来表示,相似度越高,距离在越小。因此,定义xi,xj,间的相似度为
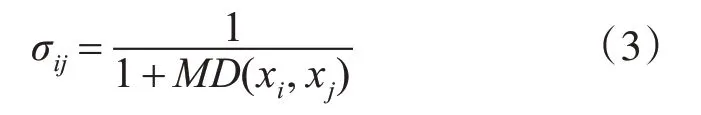
定义样本自身的相似度为0,即当i=j时,σij=0。
3.2 基于流形距离的邻域选择
根据定义,数据集中任意两点间的流形距离,算法流程如下:
步骤1:由式(1)构建线段长度矩阵L;
步骤2:利用式(2)计算数据点对之间的流形距离,根据式(3)计算数据点对间的相似度。
步骤3:根据步骤2 计算出的相似度选择样本点xi的近邻点数。
4 基于压缩感知的稀疏表示投影
压缩感知(CS)理论的核心内容是:在某一稀疏基Ψ=[ψ1,ψ2,…,ψN]上具有m稀疏表示的进行N采样的信号x∈RN,即
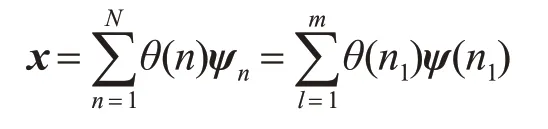
假设通过非线性映射φ将样本xi∈RN(i=1,2,…,N) 映射到高维特征空间,即φ(xi)(i=1,2,…,N) 表示非线性映射后的特征样本向量。令R=[φ(x1),φ(x2),…,φ(xN)],则下式可以描述高维特征空间的稀疏表示问题:
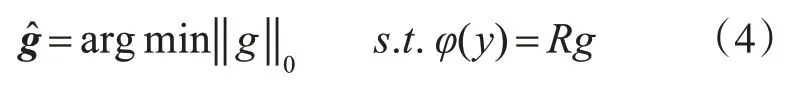
其中,φ(y)是由原空间任一样本数据y映射到高维特征空间的象。问题(4)的近似解可以通过求解以下的约束最优化问题得到:
其中,g表示高维特征空间中的稀疏表示稀疏向量。
利用核方法计算高维特征空间数据的内积,得:
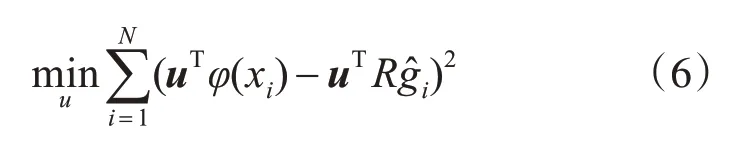
对目标函数(6)进行数学理论推导:
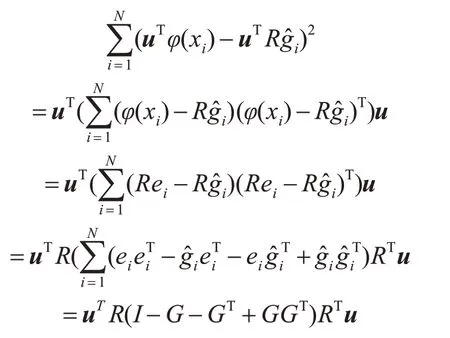
给定约束条件uTRRTu=1,则优化目标函数为
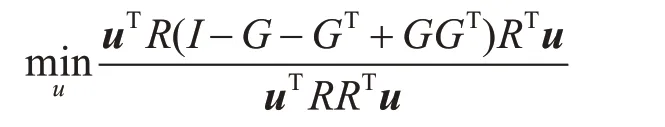
上式可等价于以下最大优化目标函数:
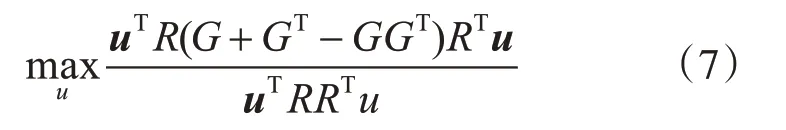
最大化目标函数(7)可以转化为求解以下特征方程:
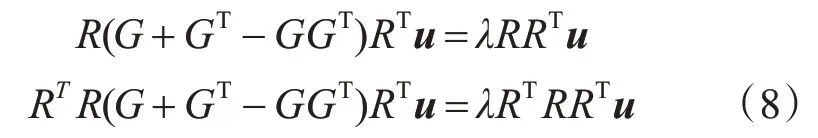
其中,投影向量u=Rp,将其代入方程(8),可得:
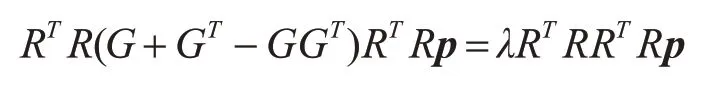
对上述特征方程进行化简,得:
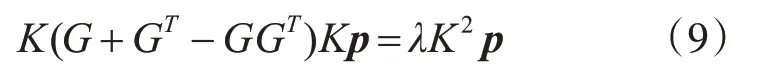
pi(i=1,2,…,d)为方程(9)对应的d个最大特征值的特征向量。
5 流形距离与压缩感知核稀疏投影的局部线性嵌入
算法步骤如下:
步骤1:构造近邻域,利用流形距离计算邻域点数。
步骤2:计算在高维空间权值矩阵W。
步骤4:求解特征方程K(G+GT-GGT)Kp=λK2p的前d个最大特征值对应的特征向量p1,p2,…,pd.
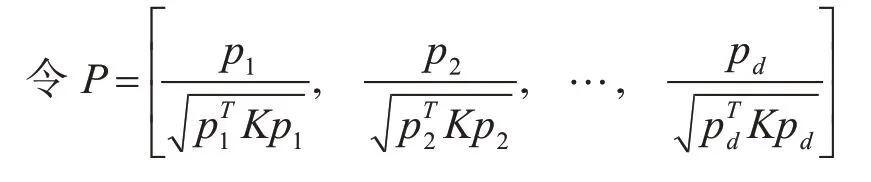
步骤5:求低维嵌入Y
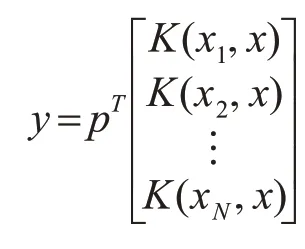
6 实验仿真
为了验证所提算法的性能,本文采用经典实验数据集Swiss roll,Swiss hold,Gaussion,Corner Planes 来说明本文提出的算法能够有效地处理非线性流形数据集。数据集的采样点数N=2000,分别选取邻域参数k=14,k=20,k=26。实验结果如图1,2,3 所示。图中分别给出了数据集 Swiss roll,Swiss hold,Gaussion,Corner Planes 在不同邻域参数k下的低维嵌入结果。从图中可以看出改进的LLE算法较原LLE算法性能有所改善,能够得到良好的低维嵌入结果,在一定范围内低维嵌入结果具有稳定性,对邻域参数K 敏感度低。如图2 所示为不同邻域参数下改进的LLE 方法的降维效果,其中(a)为加入噪声的Swiss roll 数据集,与图1 所示的不同邻域参数下LLE 方法的降维效果相比较可得出本文提出的算法对含噪数据集Swiss roll 有良好的降维结果,能够很好地发现Swiss roll数据集的内在流形结构。如图3 所示,(a1),(a2),(a3)为其他三种经典的含噪数据集。改进的LLE 算法对四种经典数据集的降维不依赖于邻域参数的变化而变化,即对邻域参数的选取不太敏感,可以达到很好的降维效果,而且对Swiss hold 数据集可以很好地反映数据集中的空洞,对不同的参数k 可以达到稳定的降维效果,如图3(b1),(c1),(d1)所示,横坐标为x轴,纵坐标为y轴。该算法对实验数据集Gaussian、Corner Planes 等也具有良好的二维嵌入结果。说明流形距离的测试能有效克服原始LLE 算法对邻域参数的敏感问题,能够创建正确反映流形结构的领域图;基于压缩感知的核稀疏投影可以实现低维嵌入时的降噪过程,并且可以很好地发现Swiss hold、Swiss hold、Gaussian、Corner Planes 四种数据集的内在流形结构。
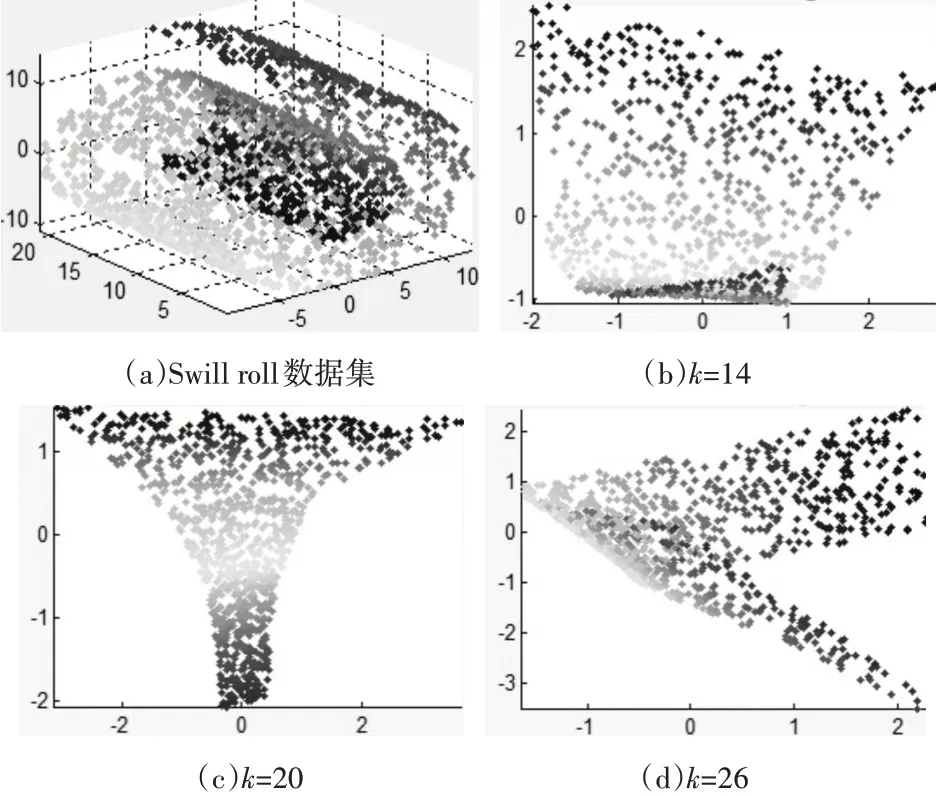
图1 不同邻域参数下LLE方法的降维效果
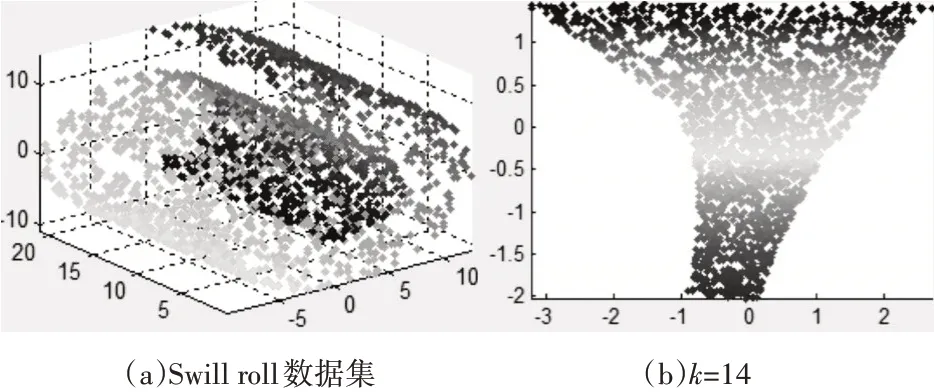
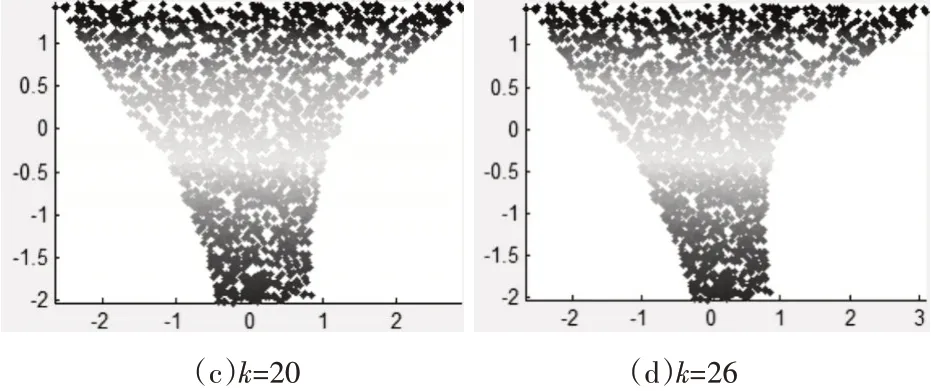
图2 不同邻域参数下改进的LLE方法的降维效果
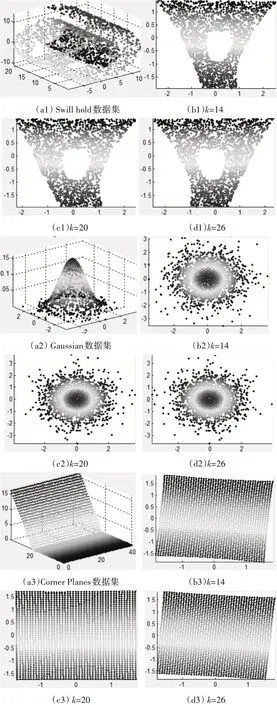
图3 不同邻域参数下改进的LLE方法的降维效果
7 结语
本文针对局部线性嵌入算法中邻域参数选择问题,提出了一种基于流形距离的邻域选择算法,该算法用流形距离代替传统的欧氏距离作为相似性度量,利用流形距离测度合理地选取各个样本的近邻点。采用基于压缩感知理论的核稀疏投影作为高维观测空间到低维嵌入空间的映射。结合上述两种思想对局部线性嵌入算法进行改进,实现高维数据的降维。实验结果表明,本文提出的流形距离与压缩感知核稀疏投影相结合的局部线性嵌入算法可以有效避免原始局部线性嵌入算法对选取近邻参数K 的不确定性及对噪声的敏感性,可以很好地发现高维数据集上的内在流形结构。
稀疏投影作为一种高维空间到低维空间的映射,可以实现数据集在稀疏采样时的邻域选择问题。后续工作将主要研究稀疏采样时邻域的选取并将核稀疏投影引入到其他几种经典的流形学习算法中。

