基于支持向量机的备件需求预测研究*
董 琪 赵建忠 隋江波 朱良明
(海军航空大学 烟台 264001)
1 引言
随着武器装备实战化需求的不断提高,备件精确化保障的重要性逐步凸显,越来越受到重视[1]。关重件作为装备的关键部件,具有价格昂贵、消耗量不大、对可靠性要求高的特点。基于统计学的需求预测方法是建立在大样本的统计数据基础上展开的,其中指数平滑法因其原理易懂、操作方便,是装备保障需求分析中最常用的方法,主要包括一次指数平滑法(简单指数平滑法)、二次指数平滑法和三次指数平滑法[2~5]。但这类方法在处理小样本数据时,预测精度常偏差较大,预测结果不理想。
综上所述,为提高小样本备件预测精度,本文以回归原理作为预测基础,结合支持向量机方法对装备备件进行预测,同时分析了不同参数优化方法对预测结果的影响。最后,通过几种方法预测结果的对比,验证本文方法的优越性和有效性。
2 指数平滑法
指数平滑法的核心思想是重点考虑了数据的“时效”,即越近期的数据,对未来的影响就越大,且不同时间数据对未来的影响程度呈非线性趋势。此外,为了提高预测精度,指数平滑法利用“误差反馈”原理,通过引入平滑系数α(0 ≤α≤1)来反映不同时间数据对于未来的权重,α越大,就表示近期观测值的权重也越大[6],不断用预测误差来纠正新的预测值。因此,平滑系数的取值对预测结果影响较大。α值越小,预测值越平滑;α越大,预测值就越敏感。
2.1 预测模型
设yi为第i期实际需求为第i期需求预测值 (i=1,…,t),时间序列为yt,α为平滑系数。预测模型(即第t期指数平滑值作为t+1期的预测值)为

由式(1)可知,当期指数平滑值取决于当期实际值和上一期的指数平滑值。具体结果则依赖α的取值,它决定了当期实际值和上一期的指数平滑值对于结果影响的比重,而不需要很多的时间序列数据。
2.2 平滑系数的选择
由此可见,平滑系数取值至关重要。由式(1)可知,α值越大,新数据所占的比重就愈大,原预测值所占的比重就愈小,反之则相反。因此,α的大小则体现了预测误差对原预测值进行修正的幅度,α值愈大,修正幅度愈大;α值愈小,修正幅度愈小。
若选取α=0 ,则。
即下期预测值就等于本期预测值,在预测过程中不考虑任何新信息;
若选取α=1,则。
即下期预测值等于本期观测值,完全不相信过去的信息,这两种极端情况很难做出正确的预测。
因此,α值应根据时间序列的具体发生在0~1之间选择。具体如何选择一般可遵循下列原则:
1)如果时间序列波动不大,比较平衡,则α应取小一点,如0.1~0.3,以减少修正幅度,使预测模型能包含较长时间序列的信息。
2)如果时间序列具有迅速且的变动倾向,则α应取一点,如0.6~0.8,使预测模型灵敏度高一些,以便迅速跟上数据的变化。
在实际操作时,需多取几个α进行试算,看哪个预测误差较小,就采用哪个α值作为权重。
2.3 初始值的确定
进行预测时,除了选择合适的平滑系数外,还要确定初始值。初始值的确定原则与样本量相关,即当时间序列的数据较多(20 个以上时),初始值对预测结果影响很小,可选用第一期数据为初始值;当时间序列的数据较少(20 个以下时),初始值对预测值影响很大,就必须认真研究如何正确确定初始值。一般以最初几期实际值的平均值作为初始值[7]。
3 基于支持向量机的备件需求预测模型构建
支持向量机(SVM)方法以结构风险最小化(SRM)为原则,可将预测问题转化为凸二次规划问题求解,保证得到的极值就是全局最优解,一方面可以有效地克服过学习问题,另一方面又可以防止造成维数灾难,在解决小样本学习问题上具有神经网络等方法不可比拟的优势[8~10]。
假设以备件的历史需求数据作为输入,以下一期需求量作为输出,建立基于支持向量机的备件需求预测模型,其基本步骤如下(流程图见图1)。
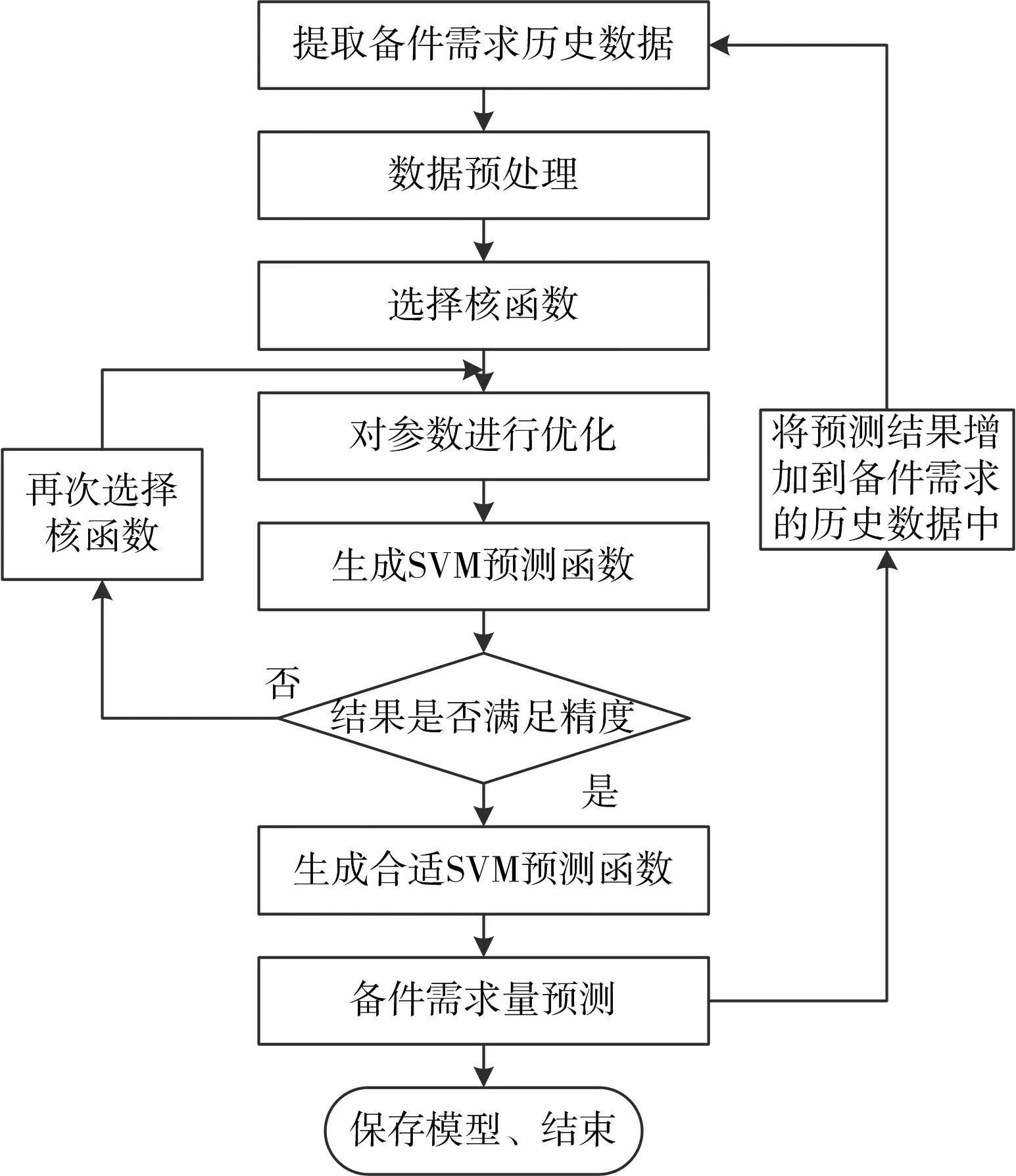
图1 基于时间序列的支持向量机备件需求预测流程
Step1:提取备件需求x的历史数据表示第i期的备件需求 ,i=1,2,…,n。
Step2:运用极差变换法对历史数据进行预处理,使其变为[0 ,1] 区间的数值。
Step3:确定核函数,并优化参数。
Step4:确定SVM预测函数。
Step5:将预测样本代入回归函数进行备件需求预测,并对预测结果的精度进行分析,若不能达到要求的精度,重新选择核函数,转Step4;若达到精度要求,生成合适的SVM预测函数。
Step6:实施预测,并将结果增加到备件需求的历史数据中,保存模型。
根据上述建模流程,通过Matlab2008a 软件的libsvm 工具箱[11]来设计并实现仿真程序,本文首先用指数平滑法对备件的需求数据进行预测,然后分别使用网格搜索法和遗传算法对支持向量机的核参数g和惩罚系数C进行寻优,然后将两种方法优化参数的支持向量机预测模型对备件的历史需求数据进行需求预测,最后将3 种方法得到的预测数据进行对比。
为了减少误差,本文采用极差变换法对历史需求数据进行归一化处理[12]:
1)确定历史需求数据中的最大值和最小值,分别记为MAX,MIN;
2)将第t年的需求量Xt转化为:=。
4 需求量预测准确度评价
预测准确度是衡量预测方法精度的评价指标,平均绝对误差(MAE,Mean Absolute Eror)、均方误差(MSE,Mean Squared Error)以及正则化均方误差(NMSE,Normalized Mean Squared Error)均是常见的评价标准。
评价指标计算如下:
根据上述定义可知,MAE、MSE 以及 NMSE 的评价思路是相似的,即值越小,表明预测值与实际值的按拟合精度越高,则预测的准确度越高。因此,本文以MSE作为代表进行评价。
5 实例分析
通过统计某型装备的关重件消耗数据,以领用量作为备件的需求量,得到的该型装备备件的需求序列(以年为单位),如表1所示。
由图1 数据得到备件的需求趋势图,如图2 所示。

表1 备件历史需求数据

图2 备件历史需求数据
利用极差变换法,将备件历史需求数据进行归一化处理,得到表2。

表2 备件归一化处理后的备件历史需求数据
处理后的备件需求曲线如图3所示。

图3 归一化处理后的备件历史需求数据
由图2、图3对比可知,通过极差变换归一化处理后的数据,并不改变各期需求量之间的相对关系,故不会影响到需求预测模型的构建。
采用传统的指数平滑法[13]进行备件需求预测,因数据波动较大,故平滑系数α取较大值0.8(α=0.8)。由于时间序列的数据在20 个以下,故选择一般以最初2期实际值的平均值作为初始值。
由图4 可知,预测曲线与实际需求曲线拟合程度差异较大,MSE=26.54,2009 年备件的实际需求量为13,指数平滑法预测结果为10.45,相差2.54。

图4 备件需求量预测——指数平滑法
运用支持向量机回归原理进行需求量预测[14~15]。选择RBF核函数作为核函数,采用网格搜索法对惩罚系数C和核参数g进行优化,选择C=1024 ,g=0.0315。得到网格搜索法对支持向量机参数寻优图及备件需求量预测,如图5和图6所示。
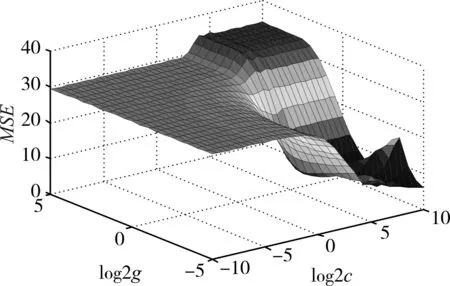
图5 网格搜索法对支持向量机参数寻优图

图6 备件需求量预测—SVM—RBF核函数
由图6 可知,预测曲线对实际数据的拟合程度优于指数平滑法,MSE=7.191,预测结果为12.31个,相差0.69个,与实际情况相符。
将参数优化的方法改为遗传算法,选择C=121.0345,g=0.4983 进行需求量预测,得到适应度函数图7及备件需求量预测曲线图8。

图7 适应度函数

图8 备件需求量预测-GA-SVM需求预测-RBF核
由图8 可知,预测曲线与实际数据的拟合程度与网格搜索法相近,均优于指数平滑法,MSE=5.398 ,预测结果为12.43 个,相差0.57 个,略优于网格搜索法。
将各方法计算的结果进行对比分析,得到表3。
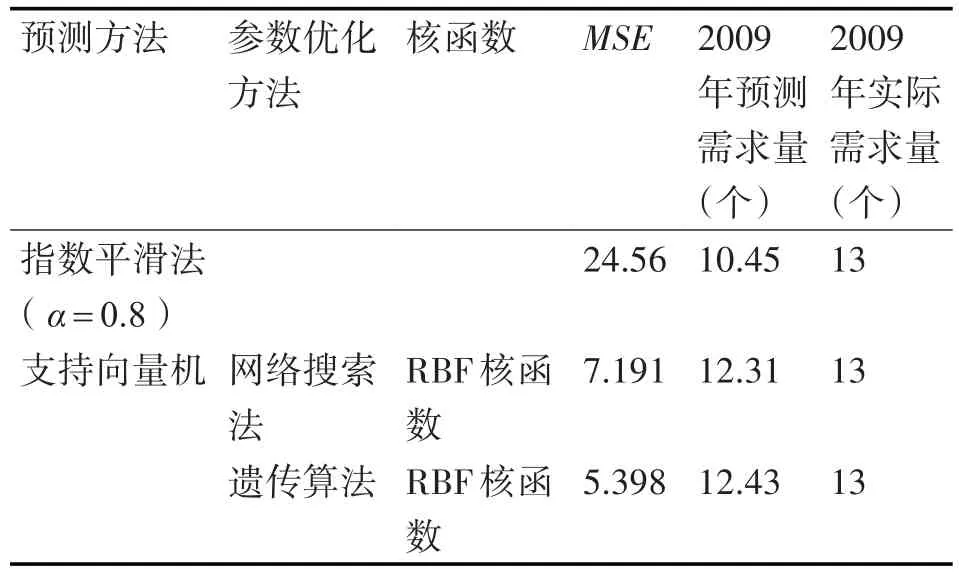
表3 预测结果对比表
由表3 可知,指数平滑法的预测效果较差,MSE为24.56,支持向量机的预测效果很好,当采用网格搜索法来优化参数时,MSE为7.191,当采用遗传算法来优化参数时,支持向量机预测性能最好,MSE达到5.398。
6 结语
根据支持向量机回归原理,建立了基于支持向量机的备件需求预测模型,以及需求预测准确率的评价指标。由实例数据结果得出以下结论:
1)支持向量机的预测性能远远优于传统的指数平滑法。
2)采用SVM 方法预测时,遗传算法优化参数后的预测准确率略高于网格搜索法。
因此,运用遗传算法优化的支持向量机能够较好地解决小样本备件的需求预测问题。

