巧构中线妙解几何题

王保华

摘要：三角形是初中数学里最基本的几何图形，中线是三角形中重要的线段之一。在与中线有关的题构思巧妙，具有探索性，其目的在于考查学生的想象能力，培养学生的创造性，值得关注。

关键词：中线   倍长中线

解法几何题中有关三角形中线问题构思巧妙，解法多样且灵活，技巧性强，具有探索性。本文结合实例就中线常见的辅助线归纳，试探索不同的三角形中线有关几何图形的解法，介绍一些常用方法和技巧。

一、三角形中线把原三角形分成两个面积相等的小三角形

例1：如图1，在△ABC中，已知点D、E、F分别为边BC、AD、CE 的中点，且△ABC的面积是32，则图中阴影部分面积等于________________

解：∵点D、E、F分别为边BC，AD，CE的中点，∴S△ABD= 12S△ABC、S△BDE= 12S△ABD、S△CDE= 12S△ADC、S△BEF= 12S△BEC，∴S△BEF= 14S△ABC;∵△ABC的面积是32，∴S△BEF=8。

评注：本题主要考查了三角形面积问题，首先应该联想到角形的中线把原三角形分成两个面积相等的小三角形（等底同高），然后通过探索，找准中点，连好中线，解决问题。

2、有三角形中线时，常延长加倍中线 （倍长中线法）

“倍长中线”是指加倍延長中线，使所延长部分与中线相等，然后连接相应的顶点，由对应角对应边都对应相等，构造全等三角形，直接或间接用“倍长中线法”构造全等三角形和证明边之间的关系。

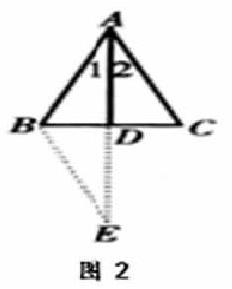
例2.如图2，已知ΔABC中，AD是∠BAC的平分线，AD又是BC边上的中线。求证：ΔABC是等腰三角形。

证明：延长AD到E，使DE=AD，连接BE在ΔACD和ΔEBD中AD=ED∠ADC=∠EDBCD=BD∴ΔBED≌ΔCAD，∴ EB=AC，∠E=∠2，又∠1=∠2，∴∠1=∠E，∴AB=EB，从而AB=AC，即ΔABC是等腰三角形。评注：此题容易进入误区，用“边边角”这一错误的判定来证明。如果出现了三角形的中线，常延长加倍此线段，再将端点连结，把所要证的线段转移到同一个三角形中，构造全等三角形，使题中分散的条件集中，进而解决问题。

三、直角三角形斜边中线的性质

例3.如图3，已知梯形ABCD中，AB//DC，AC⊥BC，AD⊥BD，求证：AC=BD。

证明：取AB的中点E，连结DE、CE，则DE、CE分别为RtΔABD，RtΔABC斜边AB上的中线， ∴DE=CE=  AB∵∠CDE=∠DCE。∵AB//DC，∴∠CDE=∠1，∠DCE=∠2，∴∠1=∠2，在ΔADE和ΔBCE中，   DE=CE∠1=∠2AE=BE∴ΔADE≌ΔBCE，∴ AD=BC，从而梯形ABCD是等腰梯形，∴AC=BD。

评注：此题易忽略“直角三角形斜边上的中线等于斜边的一半”这一重要性质，这两条中线构成一个等腰三角形，考查了学生对知识的应用和迁移能力，具有很强的灵活性。

三角形的中线在中考几何题中具有活力，巧妙利用中线一些基本图形的数学模型及其结论，是解决三角形中点问题的一个着力点。培养学生运用变化的眼光去观察图形，抓住问题本质，深入分析，灵活运用所学知识解决。

参考文献：

1.赵伟玲，三角形中线的魅力 [J]，中学生数学2019年10期

2.李海燕，“无中生有”巧构中线 [J]，初中生世界2014年31期

3.冯少华，倍长中线法及其应用 [J] ，初中生数学学习2002年26期