数学“一题一课”素材开发策略
沈正会

[摘要]通过实践研究,数学“一题一课”可以教材中的典型例题、教学中普遍出现的问题、学生作业中的典型错题、教材中的综合性习题、阶段性教学目标达成的探究材料为素材进行开发,使学生理解与掌握所学的数学知识,真正做到活学活用,促进学生数学思维的发展。
[关键词]小学数学;一题一课;素材;开发策略
[中图分类号]G623.5
[文献标识码]A
[文章编号]1007-9068(2020)18-0004-03
“一题一课”,指教师通过对一道题或某一素材的深入研究,挖掘其中蕴含的数学本质与内涵,科学、合理、有序地组织学生进行相关的数学探索活动,完成一节课的教学任务,实现引导学生感悟解题策略、积累数学活动经验、渗透数学思想方法等多维日标。“一题一课”旨在尽可能地为学生的学习起到穿针引线、线面结合、立体呈现的作用,使学生所学的数学知识形成一个完整的结构系统,最大限度地促进学生的可持续发展。
那么,怎样有效地开发数学“一题一课”的素材呢?经过多年的探索,笔者在实践中总结了一些切实可行的素材开发策略,现与大家共同分享和探究。
一、以教材中的典型例题为素材
教材是学生学习与教师教学的主要依据,所以教师应深入研读教材,充分把握教材,灵活应用并合理开发教材,帮助学生理清知识脉络,沟通知识之间的内在联系,促进学生的思维发展,构建高效课堂。数学“一题一课”的素材可以是对教材中一道典型例题的深入研究,然后由一道例题引发一堂课的教学,引导学生不断深入探究,发展学生的数学思维。
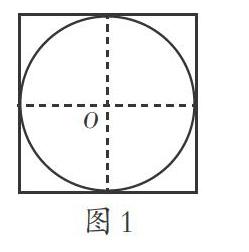
例如,教学人教版小学数学六年级上册《网的面积》一课,在教学例题“外方內网”和“外圆内方”后,教师让学生练习一道变式题(出示图1):“已知网的面积是94.2平方厘米,你能求出正方形的面积吗?”在解答这道题的过程中,学生获得新的学习体验:r2不仅是网的半径的平方,而且是一个以网的半径为边长的小正方形面积,它的面积与外切正方形面积的比为1:4。这样教学帮助学生进一步深化对所学知识的理解,提升学生的思维能力。接着,教师出示一道拓展题:“如图2,四张同样大小的正方形铁皮(边长是1.8m),分别按图3、图4、图5、图6四种方式剪出不同规格的铁片。剪完后,哪张铁皮剩下的废料多些?如图6,如果继续剪下去,剩下的废料又会是多少呢?这其中有什么规律吗?”在学生得出“铁皮按四种方式剪完后剩下的废料一样多”的结论后,教师引导学生通过字母式进行比较、分析,继而推理验证结论。这里,学生经历了由特殊到一般的探究过程,不仅掌握了解题方法,而且初步感知其中的数学思想方法。
因此,教师要对教材中的例题进行深入分析和精心设计,通过对一道例题的充分发挥,做到一题求联、一题求变,引导学生沟通数学知识之间的内在联系,使学生真正理解与掌握所学的数学知识,促进学生能力和素质的提升,让教材更好地为学生的学习服务。
二、以教学中普遍出现的问题为素材
在平时的数学教学中,经常出现这样的情况:一道题反复练习多遍,仍有学生出错,或者教师讲解题日后稍做修改,又有学生不会解答了。究其原因,是教师对学生出现的问题做简单化处理,导致学生对所学的数学知识并没有真正理解。因此,在数学教学中,教师要将学生不易理解、容易混淆的知识具体化,通过一题多变,促进学生对所学知识的理解与掌握。
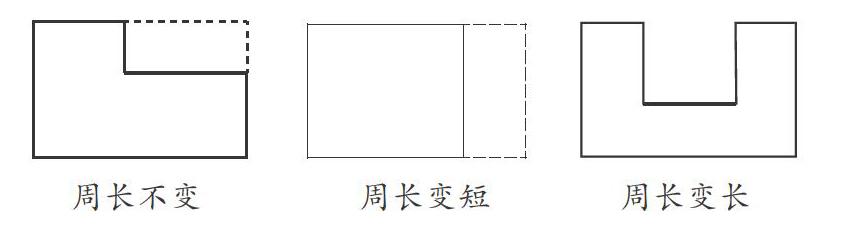
例如,很多教师认为“长方形的周长和面积的关系”这一知识比较简单,教学时轻描淡写,导致学生对这一知识并没有真正理解,时间一长,还是普遍认为“长方形的周长越长,面积就越大”。对于这一知识,教师可以设计成“一题一课”,让学生思考周长相等的长方形面积有什么不同。学生展开探索后得出结论:周长相等的长方形,面积不相等,其中正方形的面积最大。教师追问:“长方形的面积变小,那它的周长是不是会变短呢?”在大多数学生猜想长方形的周长会变短后,教师让学生在长方形纸上剪下一个小长方形进行操作验证。学生汇报时展示以下三种情况:
这样教学,学生明白“长方形的面积变小,周长有可能变短,也可能变长,还有可能不变”,从而实现了对这一知识点学习的巩固、深化和拓展。
三、以学生作业中的典型错题为素材
在平时的教学中,经常发现有些数学题学生的错误率非常高,经过教师讲评与订正后,过一段时间,很多学生还是出错。对于这类典型错题,教师反复讲解分析的话,往往收效甚微。在实践中,笔者借助“一题一课”,从不同角度分析典型错题,引导学生寻找错误的原因,不仅能使学生真正理解所学知识,提高学生思维的灵活性,而且可以实现举一反三、触类旁通的日的。
例如,四年级下册的作业本中有这样一道题:“6x(△+1.3)误写成了6×△+1.3,现在比原来差()。”此题的出错率很高,主要原因是学生的符号意识较薄弱,仅靠教师讲解,教学效果低下。笔者以“一题一课”的方式展开这道题的教学,即用几个不同数字替代△算出结果后进行比较,让学生发现替代数越小越方便。在学生提出用0替代△进行计算时,笔者顺势提问:“为什么用不同的数替代△,差都是6.5呢?用0替代,为什么能直接得到差呢?”讨论交流后,学生真正明白了:6x(△+1.3)=6×△+6x1.3,6x△+6x1.3与6x△+1.3相比,差6x1.3-1.3=6.5。这样教学,使学生深刻体会到用数字替代符号是解决问题的有效途径,能把复杂的问题简单化,且使用符号表示运算推理后得到的结论具有一般性,是代数思想的精髓所在。
因此,面对数学作业中的典型错题,教师不仅要引导学生从知识的定义、本质出发辨错,更要使学生学会对错误进行反思,寻找错误的原因。同时,教师要充分挖掘错题中的教学资源,因势利导,巧妙地将错题适度开发,精心设计成一节课,把错误变成学生学习中的新发现、闪光点,使学生真正内化所学的数学知识。
四、以教材中的综合性习题为素材
小学数学教材中有不少的开放性、综合性习题设计得非常巧妙,蕴含着数学思想方法,这些习题如果在课堂教学中进行练习,学生思考的时间少,不能很好地体现这些习题的教学价值。因此,教师可采用“一题一课”的方式,由点及线、由线及面、由一道题变成一类题,使教材中的习题成为发展学生数学思维的好素材。
例如,人教版小学数学三年级上册有这样一道题:“一张长方形纸,长30厘米,宽21厘米。从这张纸上剪下一个最大的正方形,正方形的周长是多少厘米?剩下的长方形的周长是多少厘米?”练习时,教师引导学生借助直观操作展开一系列的探究活动,自主解决自己提出的“长方形的周长是多少厘米”“怎样从长方形纸上剪下最大的正方形”等问题。在学生解决问题的过程中,教师适时追问:“原来长方形的周长是102厘米,把它分成一个最大的正方形和一个小长方形后,它们的周长分别是84厘米、60厘米,周长和为144厘米,为什么原来长方形的周长与分成后两个图形的周长之和不相等呢?”在学生回答后,教师继续提出问题:“把一张正方形纸撕成不规则的两部分,如,这两部分的周长有什么关系?把一张正方形纸折成两个一样大的长方形,每个长方形的周長是多少?用这样的两个长方形任意拼成一个图形,拼成的图形的周长是多少……”
一堂课就围绕一道题展开学习与思维活动,有利于学生保持持久的好奇心与求知欲,促使学生积极地进行数学思考。在这样的练习课中,学生的学习自然是生动活泼、主动的和富有个性的过程。
五、以阶段性教学目标达成的探究材料为素材
当完成一个板块或一个单元的教学后,教师经常会选编一些有结构性与挑战性的探究材料,让学生在问题解决过程中体会方法的多样化。同时,这样可引导学生沟通知识之间的内在联系,使学生构建完整的知识体系,实现知识迁移、发展思维的教学日标。
例如,人教版小学数学五年级上册《多边形的面积》这一单元,教学《整理与复习》时,教师出示这样一道题:“下面图中哪几个梯形的面积相等?为什么?”
首先,在学生通过计算知道第(1)个、第(2)个和第(4)个梯形的面积相等后,教师引导学生观察这三个梯形,并归纳出结论:高相等的梯形,如果上底与下底的和相等,那么面积就一定相等。其次,将第(1)个梯形的上底延长2厘米,下底缩短2厘米,变成一个平行四边形(如图7),让学生观察原来梯形和转化后的平行四边形,引导学生发现:一个梯形和一个平行四边形,如果高相等,上下底的和也相等,那么它们的面积相等。再次,将第(1)个梯形的上底缩短2厘米,下底延长2厘米,变成一个三角形(如图8),让学生思考这个三角形与原来梯形的面积关系,从而得出结论:不管是梯形、平行四边形、三角形,还是长方形、正方形,只要高相等,上下底的和也相等,那么它们的面积就相等。
最后,教师设计以下习题让学生进行巩固练习:“下面的图形面积之间有什么关系?你能画一个高和面积都与已知梯形相等,但形状不一样的图形吗?”
这样的“一题一课”教学,能够深入揭示长方形、平行四边形、三角形和梯形等平面图形面积之间的内在联系,帮助学生构建完整的知识体系,使学生的思维不断得到发展。
综上所述,在“一题一课”的教学设计和实施过程中,教师要特别注意以下几点:一是理序,即在吃透教材、读懂学生的基础上,深入剖析和研究习题的内涵与外延,充分挖掘习题的功效,做到“借题发挥,题尽其用”;二是悟本,即巧用一题引导学生梳理所学的数学知识并结点成网,建构完整的数学知识体系,使学生明晰数学的本质,感受到数学学习的乐趣;三是促思,使学生能够通过“做一题,通一类,会一片”,真正做到活学活用,促进数学思维发展。
[参考文献]
[1]吴建成.于方圆之境,育空间之心[J].小学数学教师,2017(11).
[2]胥传翠.多边形的面积计算教学反思与实践[J].小学数学教师,2011(06).
(责编 杜华)

