基于随机森林回归方法的水稻产量遥感估算

杨北萍 陈圣波 于海洋 安 秦 (吉林大学 地球探测科学与技术学院，长春 130012)

摘 要 为寻求高效的水稻产量估算方法，以2017年长春市九台和德惠地区的采样点为样本，遥感数据和气象数据为特征变量，通过对产量与特征变量间的相关性分析与特征变量之间的主成分分析和袋外数据(out-of-data,OOB)变量的重要性分析对特征变量进行选择，以选择后的特征变量为输入变量建立水稻产量估算的随机森林回归(RFR)模型。结果表明：特征变量优选后的RFR模型对水稻产量估算的精度更高，决定系数R2和平均相对误差MRE分别为0.950和0.060；并将该模型应用到农安地区，以多元逐步回归模型作为比较模型，表明RFR模型的水稻产量估算精度明显优于多元逐步回归模型，RFR模型的R2和MRE分别为0.730和0.090，多元逐步回归模型的R2和MRE分别为0.530和0.120。

水稻是我国的主要粮食作物之一，水稻产量的多少直接关系着农民的生活保障以及农业经济的发展进程，随着农业经济的发展，水稻产量估算费时费力的方法已经难以满足农业经济发展的需求，所以找寻水稻产量及时、准确的估算方法也越来越重要。遥感作为一种新兴的探测技术，能够准确快速的收集信息，目前，越来越多的研究学者利用遥感手段获取信息来进行农作物产量估算方面的研究。Hamar等[1]基于Landsat影像获取的不同遥感植被指数与玉米和小麦的产量建立了线性回归模型；洪雪[2]基于高光谱遥感数据的植被指数建立了水稻的产量关系模型，汤斌等[3]基于遥感和气象数据对江苏省水稻面积监测和估产进行了研究，但限于不同模型的选择虽采用了遥感技术但在产量估算精度上仍存在较大差异。

随机森林回归(Random forest regression，RFR)模型是一种基于机器学习的统计方法，它能处理很高维度的数据并且估算结果具有较高的准确率。据此已有国内外研究学者将该方法应用于农业遥感估算上来。王丽爱等[4]基于RFR模型结合多种植被指数对小麦叶片SPAD值进行了遥感估算，结果表明RFR模型对比支持向量回归模型和BP神经网络模型表现了最强的学习能力；张伟等[5]基于遥感影像数据和样地调查数据利用RFR模型对江山市公益林生物量进行了估算，估算精度较高。Jeong等[6]应用RFR模型通过多种变量的输入对全球农作物的产量进行了估算，结果显示RFR模型是一种高效、可靠地估算方法。然而在目前的研究中应用RFR模型对农作物单点产量进行估算的研究还相对较少，并且大部分学者应用RFR模型进行估算时，均采用特征变量直接输入的方式，并未对特征变量进行分析。

本研究以遥感数据以及气象数据作为特征变量，通过对产量与特征变量间的相关性分析、特征变量之间的主成分分析和OOB变量重要性分析，选择最优数据作为输入的特征变量建立水稻产量估算的RFR模型，以期提高利用该模型进行水稻产量估算的精度。

1 材料与方法

1.1 研究区概况

研究区为长春市九台、德惠以及农安地区，是吉林省水稻主产区，位于125°14′～126°30′E，43°50′～44°55′N。研究区气候以温带大陆性季风气候为主，2017年最高气温35 ℃，最低气温-29 ℃，年平均气温6 ℃；日平均降水量6.7 mm，累积降水量为1 423.9 mm，降水主要集中在6—9月；累积太阳总辐射达到7 923.44 MJ/m2。

1.2 数据获取

1.2.1遥感数据

水稻从生长到成熟主要经历出苗、分蘖、抽穗、灌浆和成熟5个生育期，由于HJ-1A/B和Landsat8卫星遥感数据空间分辨率相同，本研究从HJ-1A/B和Landsat8卫星数据中获取2017年水稻全生育期(growing-season，GS)的遥感图像，使用ENVI软件对HJ-1A/B卫星数据以及Landsat卫星数据进行预处理，主要包括正射校正、辐射定标、大气校正。将原始多光谱图像的DN值转换为辐射亮度值。表1 为2种遥感数据来源以及影像获取时间。本研究选择HJ-1A/B卫星和Landsat8卫星光谱覆盖范围内的蓝光波段(B1)、绿光波段(B2)、红光波段(B3)、近红外波段(B4)反射率数据以及由这4个波段构建的4种植被指数和影响作物生长的光合有效辐射的吸收比例(FPAR)指数作为遥感变量[7-9]，共计45个。

表1 遥感变量及其说明Table 1 Remote sensing variable and description

注：GS(1-5)表示水稻5个生育期，例B3GS(1-5)表示5个不同生育期的红光波段反射率数值，其余变量的下角标GS(1-5)同理。FPARmax与FPARmin分别为0.950和0.001，表示植被覆盖度最大和无植被覆盖时的FPAR值，其取值与植被类型无关[10]。

Note：GS(1-5)represents 5 growth periods of rice. Example B3GS(1-5)represents the reflectance value of red light at 5 different growth periods, and the lower corner of other variablesGS(1-5)is in the same way. FPARmaxand FPARminare respectively 0.950 and 0.001, which indicates the FPAR value when vegetation coverage is maximum and without vegetation coverage, and the value is independent of vegetation type[10].

1.2.2气象数据

气候条件是影响农作物生长的关键因素并且气候条件的好坏直接影响着农作物产量的高低，这是因为农作物的生长完全或基本在自然条件下，作物的生长和发育阶段受气象因素的影响，适宜的温度降水和辐射条件才能促进作物生长，本研究选取水稻不同生育期的温度、降水以及辐射数据作为影响作物产量的特征变量。表2为气象变量及其单位，共计28个。从中国气象数据网上获取气象站点数据，包括最高温度、最低温度、平均温度、平均降水量以及日太阳辐射，将日太阳辐射进行不同生育期的累积，获得每个生育期太阳辐射累积值，将5个生育期的降水量进行累积获取生育期总降水量，根据日平均温度计算8月平均温度，并利用ARCGIS软件通过反距离权重的插值方法插值出与遥感数据分辨率相同的30 m分辨率的矢量，并从矢量中提取研究区内各采样点的气象信息。

1.2.3实测数据

2017年在研究区内选择了多个水稻采样点，记录水稻的有效株数和采集水稻真实样品，并进行脱粒、烘干和称重等操作。根据水稻的有效株数和重量来计算水稻的实际产量。本研究九台德惠地区共收集16个水稻采样点，农安地区6个水稻采样点，图1 为研究区2017年水稻采样点分布图。

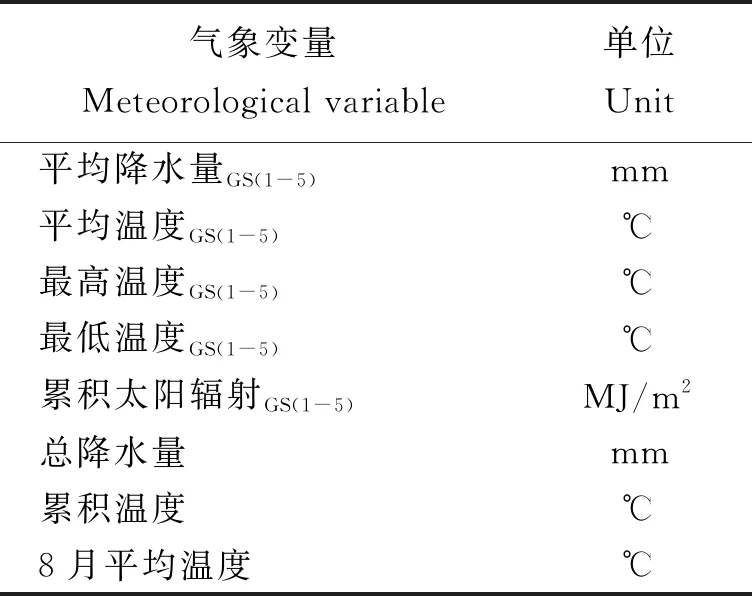
表2 气象变量及其单位Table 3 Meteorological variables and their units

注：GS(1-5)表示水稻5个生育期，例平均降水量GS(1-5)表示每个不同生育期内的平均降水量，其余变量的下角标GS(1-5)同理。

Note：GS(1-5)refers to the five growth periods of rice, 平均降水量GS(1-5)refers to the average precipitation in each different growth period, and the lower cornerGS(1-5)of the other variables is the same.

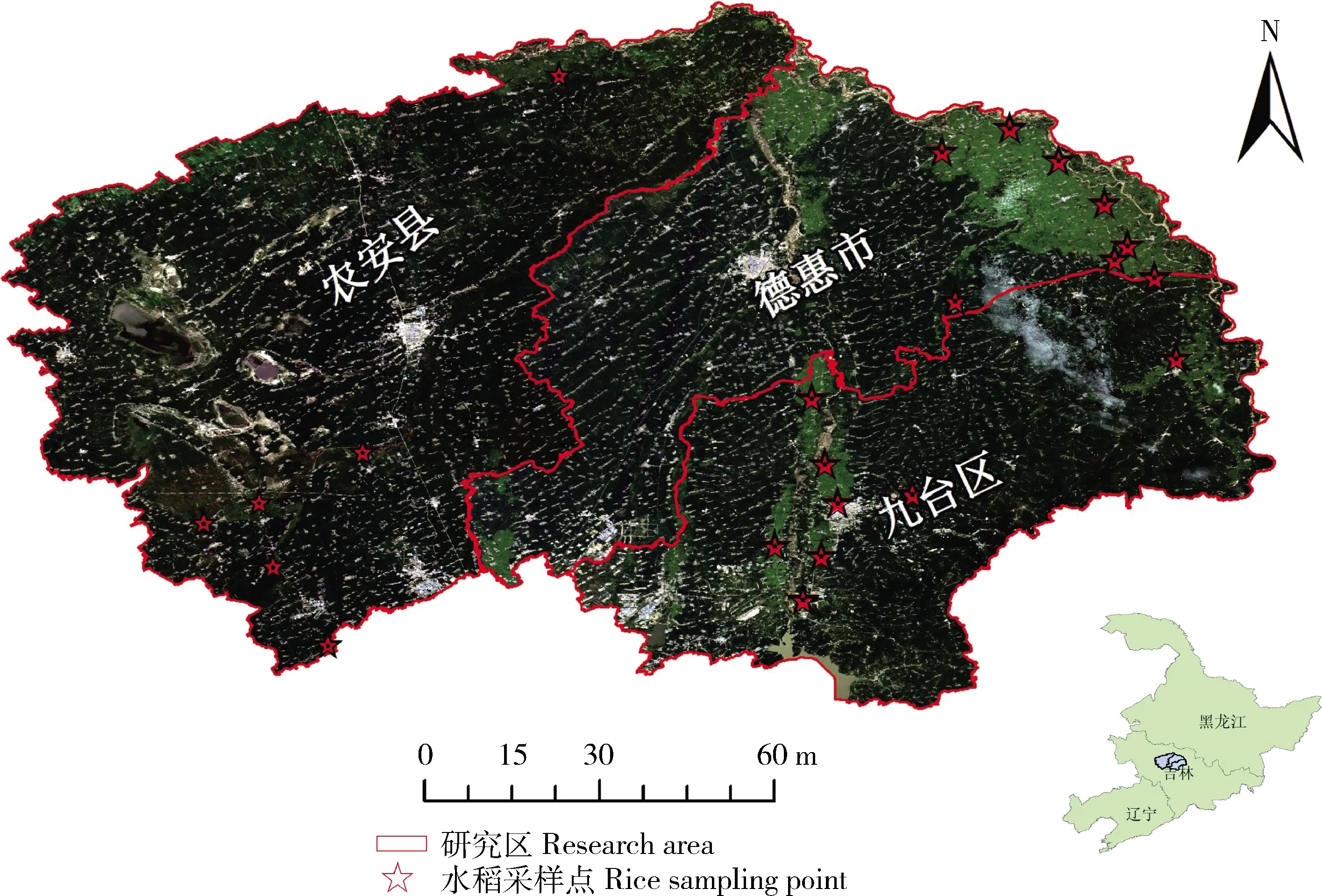
图1 研究区2017水稻采样点分布图
Fig.1 Distribution map of 2017 rice sampling sites in the research area

1.3 研究方法

随机森林回归模型原理流程图如图2所示。

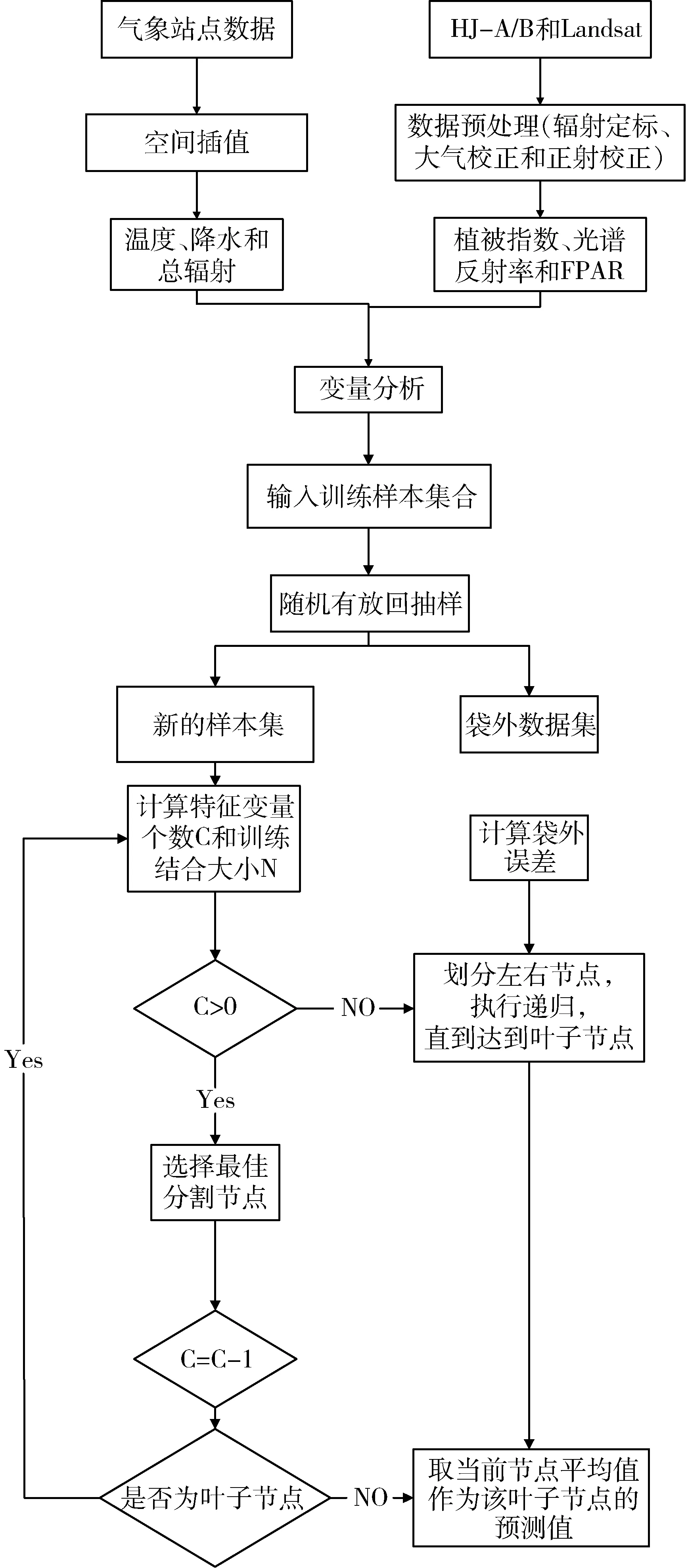
图2 RFR模型原理流程图
Fig.2 Flowchart of model principle

1.3.1变量分析

相关性分析，通过相关系数来体现产量与特征变量之间的线性相关程度，相关系数的公式为：

(1)

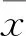
主成分分析，是将一组相关变量通过线性变换转成另一组不相关的变量，提取的主成分变量最大的包含原变量的所有信息，达到降维的目的并使得变量间相互独立。

袋外数据(out-of-bag data，OOB)重要性分析主要基于OOB数据，袋外数据是模型进行中对训练集做有放回随机抽样时每次未被抽到的样本点组成的数据集，通过袋外误差增长百分率来衡量特征变量的重要性，针对一个决策树，将OOB数据对应变量打乱前打乱后分别带入决策树[11]，计算其误差的增长百分率(IncMSE%)，假设森林中有N棵树，对于第K颗树的误差增长百分率为：

(2)

其中i为某一变量，OOBK1对应的袋外误差，OOBK2对应的打乱后袋外误差。

对于N棵树如果该变量在OOB数据上打乱后对决策树的结果没什么影响，及打乱后的均方误差的差值很小，则说明该变量不重要[12-13]。

1.3.2选择最佳分割节点

在对决策树进行分割时，设每个观测值对应n个特征，则在每一棵树的每个节点处随机从n个特征中无放回的随机抽取m个特征(m≤n)，选择一个最佳分割属性作为节点创建决策树，对于回归模型，最佳分割属性的评判标准为使分割后两部分样本的均方差结果达到最小，然后在分叉的2个节点处再利用这样的准则，选择之后的分割属性，且分割过程不需要剪枝[14-17]，直到达到叶子节点为止。

1.3.3模型参数确定

RFR模型对研究区水稻产量的估算借助于R语言中的Random Forest程序包，在该模型中主要有2个参数需要确定：决策树个数以及随机选择的变量个数m。回归树个数将直接影响预测结果的误差，但当决策树的个数为一个合适的数值时，袋外误差的变化将趋于恒定不变，本研究RFR模型中决策树的个数均根据决策树个数与误差的关系图确定，如图3所示。随机选择的变量个数程序包一般默认为总变量的1/3[18]。

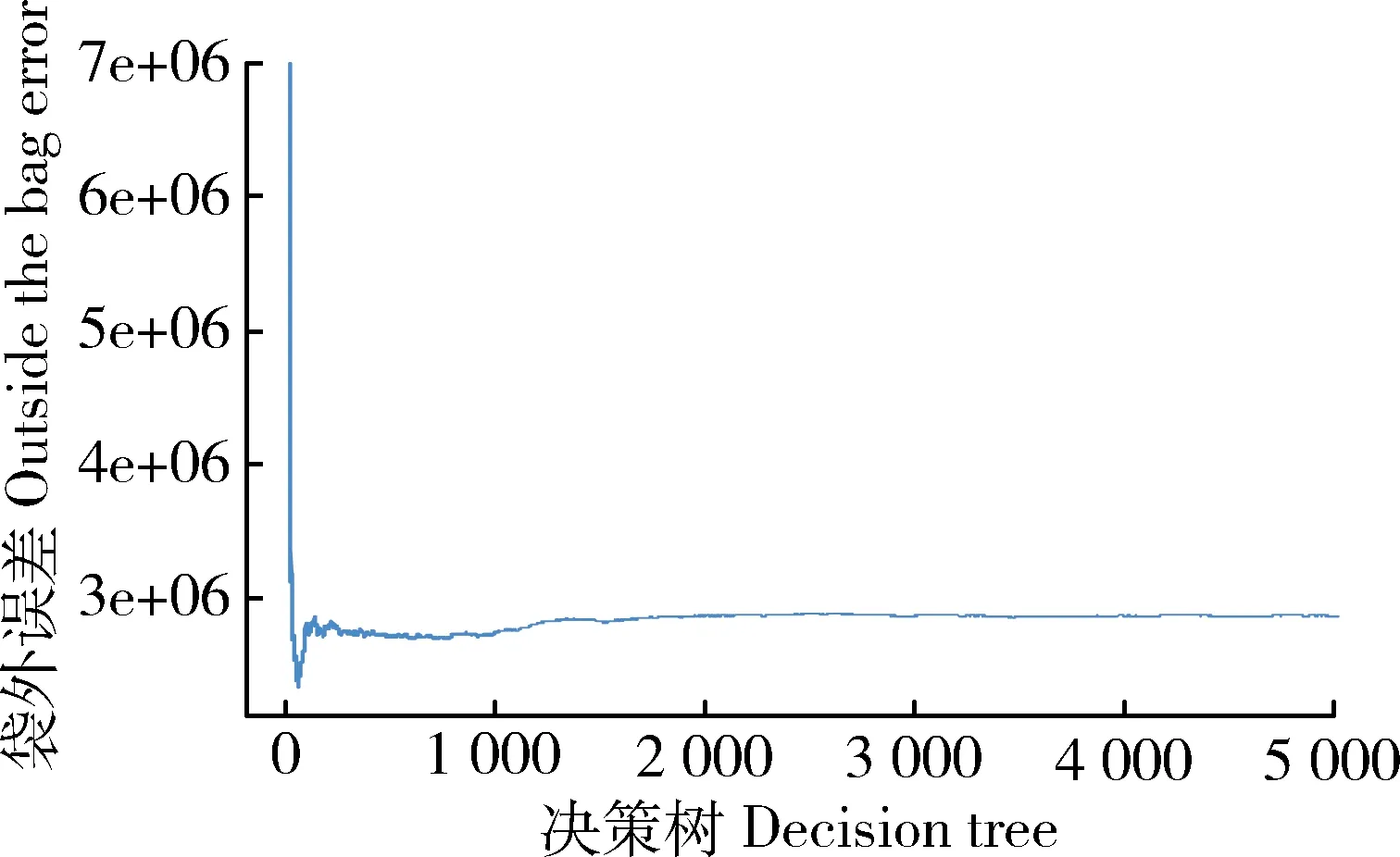
图3 决策树与袋外误差关系图
Fig.3 Relation between decision tree and outside bag error

1.3.4水稻产量估算的RFR模型建立

首先应用九台德惠地区的采样点进行建模，由于模型输入变量不同水稻产量估算结果也不尽相同，针对变量选择的不同分别建立了不同水稻产量估算的随机森林回归模型。首先用全部73个变量作为模型的输入变量，建立水稻产量估算的RFR1模型；其次分析全部特征变量与产量之间的相关性，提取15个相关性较高的变量(其相关性>0.6)建立水稻产量估算的RFR2模型；其提取的15个变量与产量的相关性表3所示；对该15个相关性高的变量进行主成分分析，提取3个主成分分析结果，累计贡献率为86.040%，建立水稻产量估算的RFR3模型；在RFR2的基础上，对15个相关性高的变量进行了重要性排序分析，剔除变量重要性排序低的变量(%IncMSE为负值)，将剩余变量重新作为输入变量建立了RFR4模型。特征变量重要性排序图如图4所示。与此同时，对全部原始变量进行主成分分析，提取了10个主成分，累计贡献率为96.670%，以这10个主成分作为模型输入变量，建立水稻产量估算的RFR5模型；对10个主成分与水稻产量间进行相关性分析，发现只有第二主成分与产量的相关性较大(相关系数为0.638)，以第二主成分为输入变量建立RFR6模型。

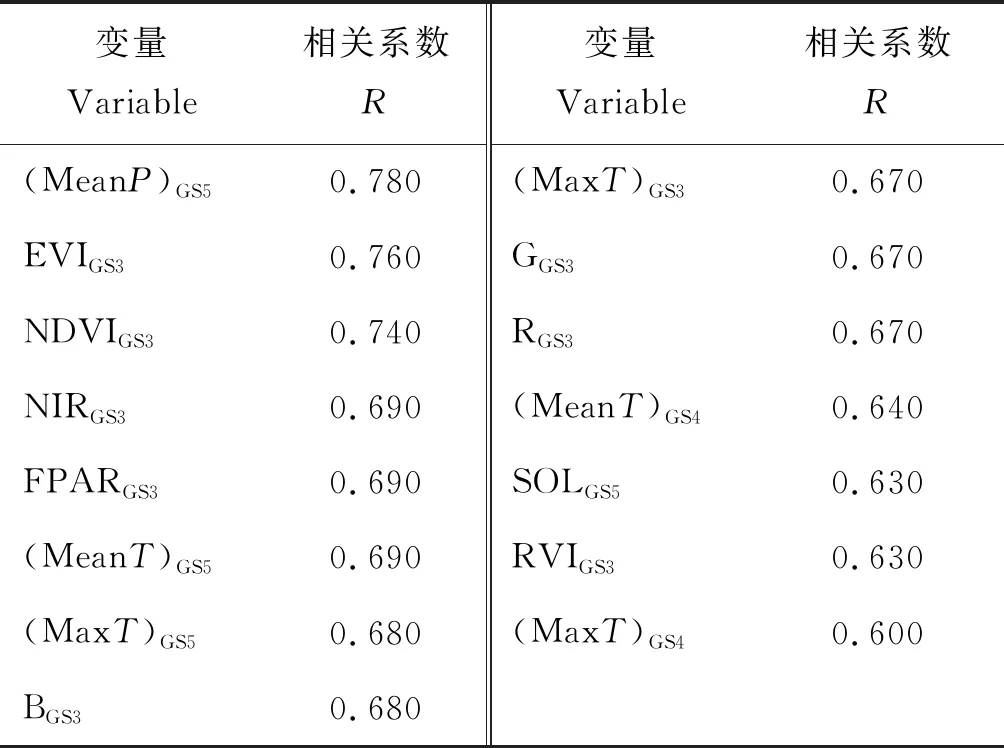
表3 水稻产量与特征变量相关性表Table 3 Correlation Table of rice yield and characteristic variables

图4 特征变量重要性排序图
Fig.4 Ranking diagram of importance of feature variables

1.4 模型精度评价

1.4.1留一法交叉验证

对于输入变量不同而建立的模型分别应用留一法进行交叉验证，每次选出一个样本进行验证，其他样本全部作为训练样本，然后建模并验证一个测试样本的估算精度以及误差，直至所有样本均参与了验证[13]，该实验有16个水稻样本点，每个模型均将进行16次的交叉验证。避免了因样本选择出现的偶然性，可以有效的对模型的稳定性进行评价。

1.4.2决定系数

决定系数(coefficient of determination,R2)也称拟合优度，是相关系数的平方，它的大小决定了相关的密切程度，R2越接近1，表示2个数据拟合优度越好，相反，越接近0，表示拟合结果越差。

1.4.3平均相对误差

平均相对误差(MRE)是多个样本测量值与估算值之间相对误差的平均值，用来作为评价水稻产量估算的结果与实测产量间的误差的一个标准，其计算公式为

(3)

式中：xm表示水稻产量测量值，xe表示产量估算值，N表示样本个数，本研究中对水稻产量的估算，MRE越小表示估算结果精度越高。

2 结果与分析

2.1 模型精度分析

利用留一法交叉验证的方法，每次选出一个样本进行验证，各模型水稻产量估算的训练集和验证集的平均相对误差变化如图5所示，其中，验证集的平均相对误差呈现逐渐减小的趋势，训练集的平均相对误差趋于恒定，研究区水稻样本点各模型的水稻产量估算值与实测值的对比如图6所示，其中RFR3模型产量估算结果满足关系式：y=0.730 3x+1 868.4，R2为0.949，相比于其他模型最高，平均相对误差为0.064，对比于其他模型最小；而剩余模型中RFR1模型对比于RFR2模型精度较高；RFR2模型对比于RFR5模型精度较高。RFR4模型以及RFR6模型对于水稻产量的估算结果精度较低。

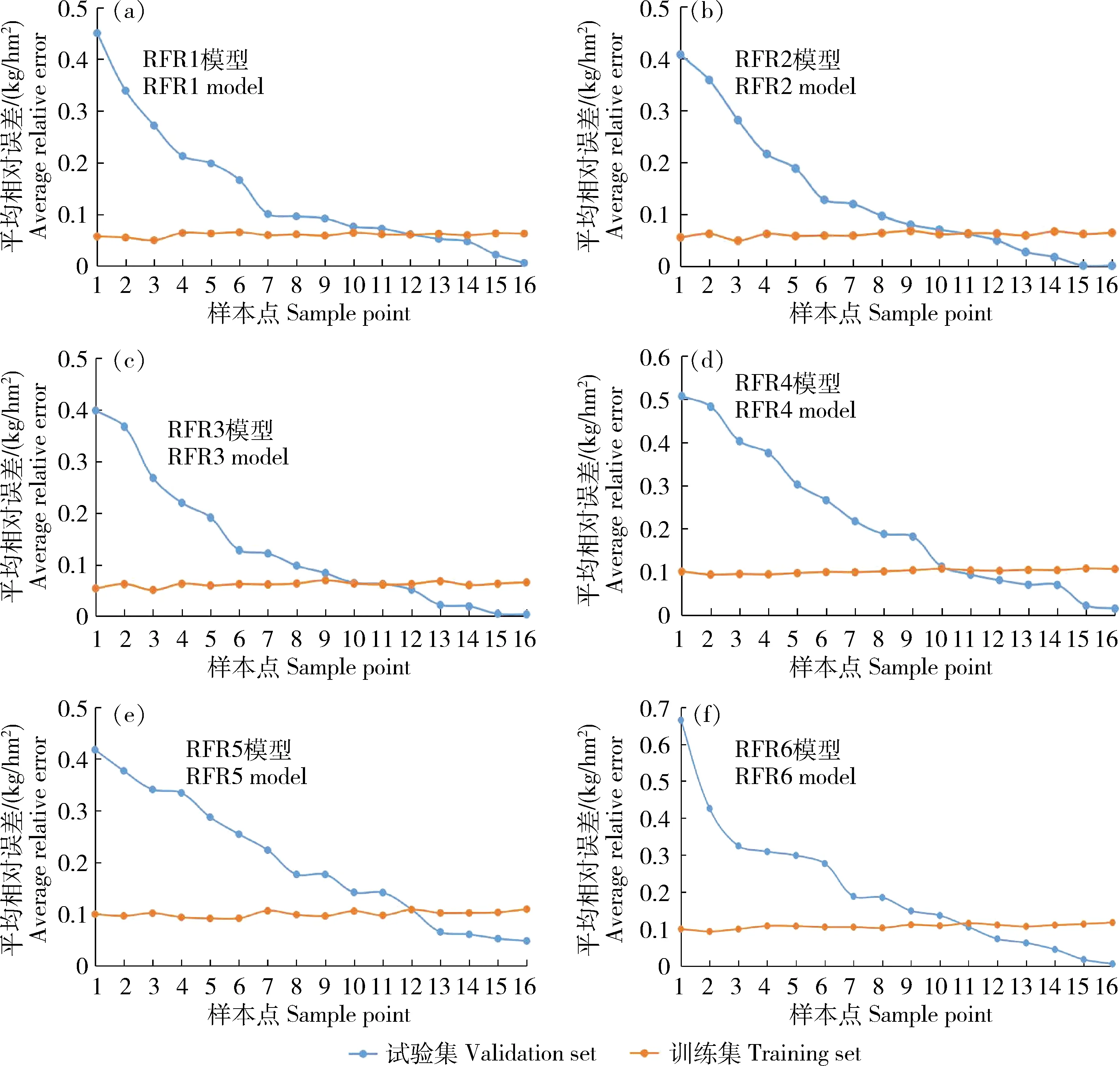
图5 水稻产量估算误差变化
Fig.5 Variation of rice yield estimation error

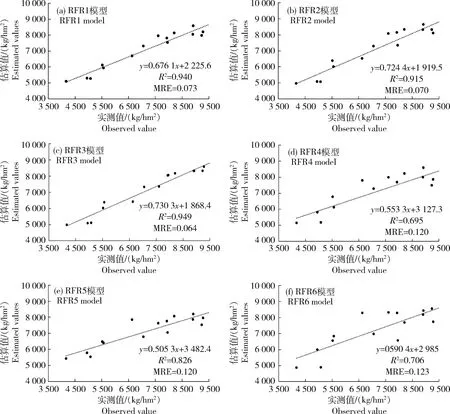
图6 水稻产量估算与实测对比
Fig.6 Comparison between rice yield estimation and observed results

2.2 模型适用性分析

由上分析可知RFR3模型水稻估算精度更好，为了进一步评判RFR3模型的适用性，在原本研究区样本点的基础上加入农安地区的6个样本点进行建模，农安地区在地形、土壤类型、以及气候类型上与研究区较为接近，并利用了SPSS软件对RFR3模型输入变量与产量间进行了多元逐步回归，逐步回归结果输入变量为第三生育期的EVI指数，移除了其余变量，关系式为：y=9 596.123×EVIGS3+980.356,将多元逐步回归结果与RFR3模型进行对比，表4为精度对比结果，结果表明应用RFR3模型对农安地区的水稻产量进行估算的结果依然较好，R2达到0.730，MRE达到0.090，明显优于多元逐步回归模型的估算精度。所以应用RFR模型估算水稻产量结果较为可靠、并且精度较高，可以很好地满足农业发展对于农作物产量估算方面的需求。

3 结 论

本研究以遥感数据以及气象数据为特征变量，通过对产量与特征变量间的相关性分析、特征变量之间的主成分分析和OOB变量重要性分析选择了最优的特征变量建立水稻产量估算的RFR模型，同时建立多元逐步回归模型与优选后的RFR模型的估算结果进行比较，进一步评价RFR模型的估算精度。研究得到以下结论：

1)应用RFR模型对研究区水稻产量估算时需要对特征变量进行选择，经过优选后的RFR模型比未优选的估算结果精度更高。特征变量的选择明显改善了模型估算精度。

2)将优选后的RFR模型应用到农安地区，农安地区的产量估算结果较好，初步验证了该模型在产量估算上的适用性。

3)优选后RFR模型对水稻产量的估算精度高于多元逐步回归的估算结果。说明优选后RFR模型能很好的估算农作物产量，为农作物产量估算方法提供新的参考。

4 讨 论

通过单一变量对产量进行估算时往往误差较大，通过图6可以发现结合多种数据进行分析，进而对农作物产量进行估算可以达到很好的效果，本研究的研究区为九台和德惠地区，仅对农安地区的采样点进行了初步验证，该模型的适用性还有待于进一步验证。本研究的输入变量为遥感方法获取反映植被生长状态的一些指数数据和气象网站获取的气象数据。然而，影响作物生长的因素众多。本研究只考虑了部分遥感数据和气象数据，在一定程度上降低了最终的估算精度。