温度－压力－吸附和煤与瓦斯突出的关系探讨

李 东，张学梅，郝静远，马青华

（西安思源学院 能源及化工大数据应用教学研究中心，陕西 西安710038）

煤与瓦斯突出事故是煤矿中最严重的灾害之一。近年来，随着煤层开采深度以每年20 m 的速度向深部发展导致采掘面冲击地压和煤与瓦斯突出2种动力灾害之间的相互影响越来越加剧，其产生的机理变得更加错综复杂，监测预警以及防治难度更大。为了确定煤与瓦斯突出事故灾变机理，寻找灾变敏感指标，有探索煤的破坏程度、煤的坚固性系数、瓦斯放散初速度和煤层瓦斯压力等单项指标[1-5]，也有研究煤层区域突出的单项指标和危险性综合指标D 值和K 值[6-10]。还有学者认为煤体温度与地应力、瓦斯压力、地质条件、气候等多种因素相关，瓦斯吸附过程是放热过程不利于在温度高的环境下进行，而瓦斯解吸过程必是吸热过程不利于在温度低的环境下进行，因此煤体温度的变化可以作为预测煤与瓦斯突出的一个指标[11-16]。实际研究表明, 因为构造软煤具有高瓦斯含量、高瓦斯压力、高解吸速度、低渗透性和低力学强度的特点，真正对煤与瓦斯突出起决定作用的因素是煤层瓦斯吸附-解吸和构造软煤发育。煤与瓦斯突出涉及原生煤、构造煤与瓦斯这3 种相互共存、互为影响的固体和气体，而固体与气体之间的关联则是吸附-解吸（涉及温度-压力-吸附量）这对互为可逆的过程。因此希望用高阶原生煤和构造煤的系列等温吸附数据，从温度-压力-吸附量的新角度，用克劳修斯-克拉佩龙方程的不定积分式和计算等量吸附焓的热力学分析来判断瓦斯解吸是吸热过程，以及如何正确比较原生煤与构造煤的吸附量与表面能之关系。从而进一步探讨为什么构造煤容易发生解吸，以及埋深的影响。

1 瓦斯吸附的放热过程

计算吸附过程的摩尔吸附焓之克劳修斯-克拉佩龙方程的不定积分式为：

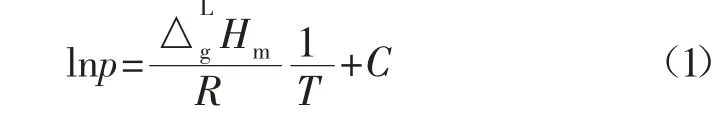
从式（1）可知，以lnp 对1/T 作图应得一直线。若直线的斜率为负值，可以判定摩尔吸附焓Hm＜0，从而判定吸附过程是放热过程。

关于摩尔吸附焓H 与摩尔吸附热Q 之间的关系与区别先作以下3 点说明：①在热力学上，焓是状态函数，即只以始态和末态有关，与途径无关，热不是状态函数，是途径函数。在热力学的推导过程只有用状态函数，如吸附焓；②摩尔吸附焓在量值上等于摩尔吸附热，等量吸附焓在量值上等于等量吸附热；③若系统从环境吸热，Q＞0，H＞0，若系统向环境放热，Q＜0，H＜0，如果等量吸附热小于0，则系统向环境放热。因此所有关于焓或热的热力学计算公式必须同时有2 个功能：既能计算结果，还能判别进行的过程是吸热还是放热。

用克劳修斯-克拉佩龙方程计算摩尔吸附焓时所用公式为：

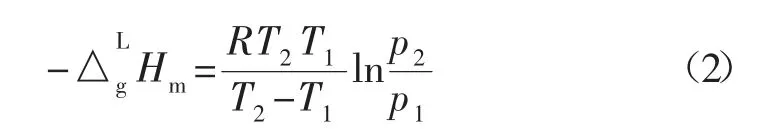
式中：T1为始态温度，K；T2为终态温度，K；p1为始态压力，MPa；p2为终态压力，MPa。

也可以用克劳修斯-克拉佩龙方程的摩尔吸附焓计算式（式（2）），判定吸附过程是吸热还是放热。如果T2＞T1和p2＞p1，式（2）的右边值大于0。要使式（2）的左边大于0，则必须摩尔吸附焓小于0，负负得正。式（2）的物理意义是：要想维持同样的吸附量，当温度升高时必然要增大气体的压力。

2 温度-压力-吸附方程

固体对气体的吸附量是温度和气体压力的函数。在恒温下，反映吸附量与平衡压力之间关系的曲线称为吸附等温线。其中最常用的是Langmuir 吸附等温方程。温度-压力-吸附方程（Temperature-Pressure-Adsorption Equation, TPAE）是一个将温度、压力、和吸附体积有机地联系起来的数学方程，旨在研究指定温度和气体压力下的煤岩或页岩吸附量变化函数关系[17-21]。

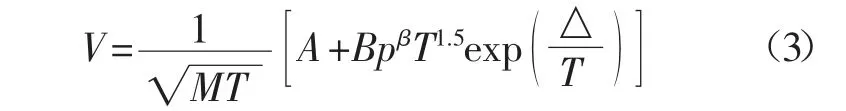
式中：V 为吸附量，cm3/g；M 为吸附分子量；A为微孔几何形体常数，无量纲；B 为吸附流量系数，无量纲；β 为压力影响的参数，无量纲；△为一个吸附分子的最低势能和活化能之间的能量差，K。

通过TPAE 做等量吸附线是将已知吸附量V 移项，将温度T 为自变量，而压力p 为因变量，得：

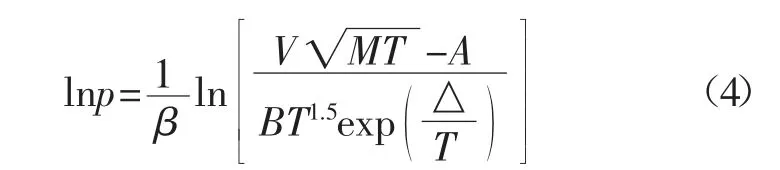
现在只要判定TPAE（式（3））可以正确地描述吸附量-吸附温度-吸附压力三者之间的关系，式（4）的表达是正确的。

3 原生煤和构造煤的等温吸附

有学者对沁水盆地南部的大宁煤矿3#煤层的原生煤和有煤与瓦斯突出构造煤作系列等温吸附实验[22]。煤样基本参数见表1，煤样的实测条件和兰氏方程参数见表2，表2 中Langmuir 参数形式的温度吸附数据变量：a 为Langmuir 体积，cm3/g；b 为Langmuir 压力的倒数，MPa-1。

表1 煤样基本参数表[22]Table 1 Basic parameters of coal samples[22]

4 结果与讨论

4.1 TPAE 的参数回归

将表1 中的兰氏参数代入Langmuir 等温吸附方程计算出回归样本群。每个温度计算10 个压力点（上限压力为10 MPa）。2 个测试温度，原生煤和构造煤各有20 个回归样本。按回归样本集的建立与计算方法[21]，用线性回归计算得到原生煤或构造煤TPAE的4 个参数A、B、△和β 和相应的平均相对误差δ。根据表1 兰氏体积和兰氏方程参数回归得到的TPAE 参数见表3。

表2 煤样的实测条件和兰氏方程参数[22]Table 2 Measurement conditions and parameters of Langmuir equation of coal samples[22]

表3 根据表1 兰氏体积和兰氏方程参数回归得TPAE 参数Table 3 TPAE parameters obtained by regression of Langmuir volume and Langmuir equation parameters in Table 1

δ 是原生煤或构造煤20 对回归样本群与计算样本群之间的相对平均误差百分数。很小的相对平均误差说明系列等温吸附实验数据可以用一个将温度、压力、和吸附体积有机地联系起来的数学方程TPAE 来描述。

除了用相对平均误差以外，也可以用作图法来显示TPAE 与系列等温吸附实验数据的吻合程度。作图法是用系列等温吸附的兰氏参数计算值为“实测点”标示在用TPAE 方程作温度-压力-吸附曲面上。原生煤的实测点与TPAE 回归曲面如图1，构造煤的实测点与TPAE 回归曲面如图2，图1 和图2就是原生煤与构造煤样的“实测点”和TPAE 曲面比较。从图中可以看出，在温度轴上显示的2 组数据表示在303、313 K 2 个温度下测试，在压力轴上的10 组数据代表每个温度计算10 个压力点。

从表3 的相对平均误差的大小以及图1 和图2点与曲面的吻合程度可以得出TPAE 能精确的表示系列等温吸附实验。

图1 原生煤的实测点与TPAE 回归曲面Fig.1 Measured points of primary coal and TPAE regression surface

图2 构造煤的实测点与TPAE 回归曲面Fig.2 Measured points of structural coal and TPAE regression surface

4.2 相同温度和压力下原生煤与构造煤吸附量比较

相同温度相同压力下原生煤与构造煤吸附量如图3。

图3 相同温度相同压力下原生煤与构造煤吸附量Fig.3 Adsorption capacity of primary coal and structural coal at the same temperature and pressure

图3 可以看出：

1）相同温度和瓦斯压力下，原生煤的甲烷吸附量略大于构造煤的吸附量; 但考虑到构造煤的坚固性系数要远小于原生煤的，这说明相同温度和瓦斯压力下构造煤比原生煤更容易被破坏，因此更容易导致瓦斯突出的发生。

2）原生煤和构造煤对甲烷气体吸附量都随着压力的升高而加大，但变化的程度是有差别的。

3）原生煤和构造煤对甲烷气体吸附量都随着温度的升高而降低，但变化的程度是有差别的。从吸附量与温度变化成负相关的特征看，吸附过程应该符合是放热过程。

4.3 相同吸附量下lnp 与1/T 的关系

吸附等量线是在吸附量恒定时，描述吸附平衡压力与温度之间函数关系。将式（4）中的吸附量恒定为5.0 cm3/g 后，假定一系列热力学温度T 可求得相应的压力。

根据克劳修斯-克拉佩龙方程的不定积分式（式（2）），按lnp 对1/T 作图，可得原生煤与构造煤样在不同吸附量时吸附压力与吸附温度的相互关系。吸附量为5.0 cm3/g 时原生煤与构造煤的lnp 与1/T 关系如图4。

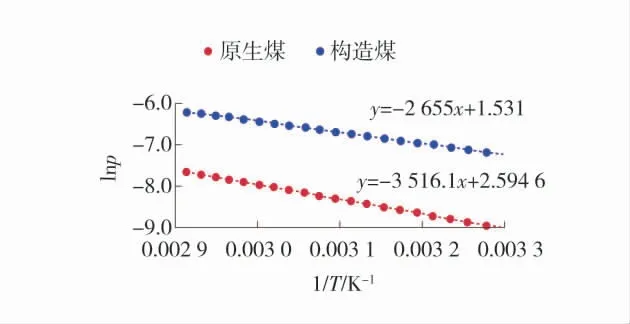
图4 吸附量为5.0 cm3/g 时原生煤与构造煤的lnp 与1/T关系Fig.4 The relationship between lnp and 1/T of primary coal and structural coal with adsorption capacity of 5.0 cm3/g

从图4 可以看出：吸附量为5.0 cm3/g 时，原生煤与构造煤的lnp 与1/T 作图得2 条具有不同负斜率的直线。也就是说，原生煤与构造煤的等量吸附焓均为负值。负斜率就说明吸附过程是放热过程。

4.4 单位等量吸附焓

1）固定单位量不一定必须是mol，也可以是瓦斯吸附中最常见的单位cm3/g。

2）要想研究原生煤与构造煤对等量吸附焓的影响，必须比较原生煤与构造煤在相同吸附量下（如5.0 cm3/g）的单位等量吸附焓（1.0 cm3/g）。

3）而研究原生煤或构造煤不同吸附量（如5.0、15.0、25.0 cm3/g 等）对吸附焓的影响，必须比较原生煤或构造煤在不同吸附量下的单位等量吸附焓。

根据吸附过程是放热过程，“单位等量吸附焓”可以理解为“单位等量吸附所放的热”。注意“吸附所放的热”是明确表示系统向环境放热，即系统自身的能量是减少的。

将煤样斜率乘以气体常数R=0.008 314 kJ/（mol·K）得在相应吸附量下的等量吸附焓，kJ/mol；将相应吸附量下等量吸附焓除以吸附量（5.0 cm3/g）得单位等量吸附焓kJ/（mol·cm3·g）。原生煤与构造煤在吸附量为5.0 cm3/g 时的单位等量吸附焓分别为-5.85、-4.42。

4.5 2 种煤在不同吸附量下的单位等量吸附焓

依次将式（4）中的吸附量恒定为等增量吸附（10.0、15.0、20.0、25.0、30.0、35.0、40.0、45.0 cm3/g）后计算一系列温度T 下所需相应的一系列压力p。作相应的lnp 与1/T 图，计算相应单位等量吸附焓。原生煤与构造煤的单位等量吸附焓与吸附量之间的相互关系如图5。等量吸附放热（吸附焓的绝对值）而下降说明：不光吸附介质（原生煤或构造煤层的裂隙与微孔）表面是不光滑的，且表面的能量是不均匀的；因为吸附是放热过程，所以吸附总是首先发生在能量较高，活性较大的位置上，随着高势能的位置被占据，然后依次发生在能量较低、活性较小的位置上。

图5 原生煤与构造煤的单位等量吸附焓与吸附量之间的相互关系Fig.5 The relationship between unit equivalent adsorption enthalpy and adsorption capacity of primary coal and structural coal

3）因为根据热力学的判定，凡是系统向环境放热，放热越多，则系统越稳定。温度高（埋藏深）对吸附不利。在吸附量都为5 cm3/g 时，原生煤的单位等量吸附放热比构造煤多放1.43 kJ/（mol·cm3·g）。而在吸附量都为45 cm3/g 时，原生煤的单位等量吸附放热比构造煤仅多放0.158 kJ/（mol·cm3·g）。

4）如果原生煤和构造煤处在完全相同的条件下（已吸附量、温度、压力等），原生煤吸附瓦斯要先于构造煤吸附瓦斯。

4.6 2 种煤在不同吸附量下的单位等量解吸焓

解吸作为吸附的逆过程，情况是完全不同。根据解吸过程是吸热过程，“单位等量解吸焓”可以理解为“单位等量解吸所吸的热”。构造煤与原生煤的单位等量解吸焓与吸附量之间的相互关系如图6。

图6 构造煤与原生煤的单位等量解吸焓与吸附量之间的相互关系Fig.6 Relationship between unit desorption enthalpy and adsorption capacity of structural coal and primary coal

1）在能量变化上解吸是吸热，而且解吸是从低能量的位置开始。根据热力学的判定，凡是系统向环境吸热，吸热越少，则系统越稳定。

2）温度高（埋藏深）对解吸有利。在吸附量都为5 cm3/g 时，构造煤的单位等量解吸吸热比原生煤要少吸1.43 kJ/（mol·cm3·g）。在吸附量都为45 cm3/g时，构造煤的单位等量解吸吸热比原生煤要少吸0.158 kJ/（mol·cm3·g）。

3）因此构造煤较原生煤更容易从冲击地压、采动卸荷、瓦斯解吸膨胀等环境中吸入能量。从而构造煤更容易受煤尘、湿度、温度、压力、火源等多因素的影响，加之，构造煤体渗透率低，非常有利瓦斯保存，也更具有重复爆炸的可能。

4）最为重要的是，当原生煤和构造煤处在完全相同的条件下（已吸附量、温度、压力等），构造煤解吸瓦斯要优先于原生煤解吸瓦斯。

5 结 论

1）根据克劳修斯-克拉佩龙方程的不定积分式或等量过程焓的计算式可判定吸附过程是放热过程，解吸过程是吸热过程。

2）温度-压力-吸附方程（Temperature-Pressure-Adsorption Equation, TPAE）可以精确描述原生煤和构造煤的温度、压力和吸附体积相互共存、互为影响的关系，并可以计算原生煤和构造煤的等量吸附焓。“单位等量吸附焓”必须理解为“单位等量吸附所放的热”。“单位等量解吸焓”必须理解为“单位等量解吸所吸的热”。

3）相较于原生煤，构造煤优先解吸；相较于放热过程，埋深强化解吸；相较于原生煤，构造煤更容易从冲击地压、采动卸荷、瓦斯解吸膨胀等环境中吸入解吸所需的能量；相较于原生煤，构造煤自身的低渗透率和低坚固性系数更容易导致煤与瓦斯突出的发生。