一种优化邻域半径的生物芯片数据处理方法

黄紫成,李 影

(仰恩大学 工程技术学院，福建 泉州 362014)

生物基因芯片也称为DNA微阵列，是当前常用的微阵列技术。微阵列所呈现的数据以矩阵形式存在，又称为基因表达数据。但是该数据存在着维数高而样本少的特征，维数通常可以达到成千上万基因，样本只有几十个，这给数据分析提出挑战。

当前越来越多的研究人员提出不同的特征选择算法应用于基因芯片数据分析中，2011年Mi H K等人提出将NMF用于肿瘤特征基因的提取[1]，2013年Song等人利用特征间相关性做权，利用普里姆算法构造出最小生成树，再选择每棵树中相关性最大的特征构成特征子集[2],2016年谢娟英等人提出基于K-S检验与mRMR原则的混合方法解决基因特征选择问题[3],2017年Lu等人为了降低基因表达数据的维度，采用最大化交互信息MIM和自适应遗传算法相结合的特征选择算法[4],Chen等人采用粗糙集和熵计算方法对基因进行特征选择[5],2018年Jain等人提出相关特征选择CFS和改进的二元粒子群iBPSO算法，对基因分类，得到较高的分类精度。

胡清华老师等人提出邻域互信息概念[6]，构造信息粒度模型，该模型能够直接处理连续型数据。在邻域模型系统，邻域的半径是影响该系统的重要因素，不同的邻域半径对模型性能有较大差别，但如何选择邻域半径并没有统一的方法。本文针对此问题，采用计算各条件属性的标准差并除以一定参数得到一组邻域半径。

1 理论介绍

粗糙集理论于1982年由波兰数学家Pawlak提出，它的观点是“知识就是一种对对象进行分类的能力”，主要思想是在保证数据分类能力不变的前提下，对数据做属性约简、特征提取等操作[7]。

下面给出几个相关定义。

定义1在给定的N维实数空间Ω中，Δ=RN×RN→R,则称Δ为RN上的一个度量，若Δ满足如下条件：

1)Δ(x1,x2)≥0，当且仅当x1=x2时取等号；

3)Δ(x1,x3)≤Δ(x1,x2)+Δ(x2,x3)

称(Ω,Δ) 为度量空间。Δ(xi,xj)表示元素xi和元素xj间的距离[6]。

定义2给定实数空间Ω上的非空有限集合U={x1,x2,…,xn}，定义邻域δ(xi)={x|x∈U,Δ(x,xi)≤δ},δ≥0，δ(xi) 称为xi的邻域粒子[6]。

定义3对于二元组NS=(U,N),∀X⊆U,X在邻域近似空间(U,N)中的上近似与下近似分别定义为：

同样定义X的下近似称为正域[6]。

定义4给定一邻域决策系统NDT=(U,A,D) ，B⊆A,在论域U中，决策属性D相对于条件属性B的依赖度定义为

而对于∀a∈A-B，a相对于B的重要度定义为[6]

西门子双源CT冠状动脉成像技术存在比较高的密度分辨率和时间分辨率高，较短的扫描时间，可提升图像质量[1-2]。西门子双源CT冠状动脉成像技术属于无创的一种影像学检查措施，在临床中已经获得诊断冠状动脉狭窄的应用价值。本次数据结果表明，诊断金标准即为冠状动脉造影(CAG)，诊断基础即为冠状动脉病变节段，可获得较好的特异性、敏感性、准确率，但也可能发生漏诊或者过诊现象，一般是由于血管细小、血管壁钙化、走形迂曲等导致的，且造影剂推注速度过快、服用硝酸甘油也可能影响诊断结果[3]。

Sig(a,B,D)=γB∪a(D)-γB(D).

2 优化邻域半径的特征基因提取算法

在基因变量中，由于实验条件因素导致存在许多噪声基因，这些基因对于分类会产生一定影响，因此，通过特征基因的提取可以去掉噪声基因，并提高分类效率，具体步骤如下：

1)根据t值统计方法，计算各基因t值

2)基于优化邻域的基因特征提取。邻域半径的选择对于特征基因的提取具有决定性作用，胡清华老师在文章[6]中对邻域半径预设一个值或是设置一定的步长范围，但这样得到的均为单一邻域半径，无法体现各属性本身的性质。因此，本文对该邻域半径进行优化改进，由于标准差能反应基因芯片数据的离散程度，为了体现各条件属性本身性质，本文计算各个基因条件属性的标准差,以此来作为邻域半径，这样对于邻域粒子的选择不再是根据固定的邻域半径，而是综合运用各条件属性的性质，并且邻域半径由单一值变为一组数据。更进一步地，为了做比较分析，得到最有效的特征基因，可以设置参数λ(如λ取0.5～1.5之间，步长为0.01)，让标准差除以λ即δ=Std(ai)/λ，这样就可以在更广泛的邻域空间内提取更有效的特征基因。

根据该组邻域半径，得到基因特征提取算法如图1所示。

图1 特征基因提取流程

该特征基因提取算法时间复杂度为条件属性个数O(n)。

3)根据提取出的特征基因数据，采用基于径向基支持向量机(SVM)和KNN分类，用分类正确的样本除以样本总数而得到识别率。

3 实验结果与分析

实验中使用基因分类常用的经典数据集Leukemia、Colon与Carcinoma[9-11]。各数据集性质见表1。

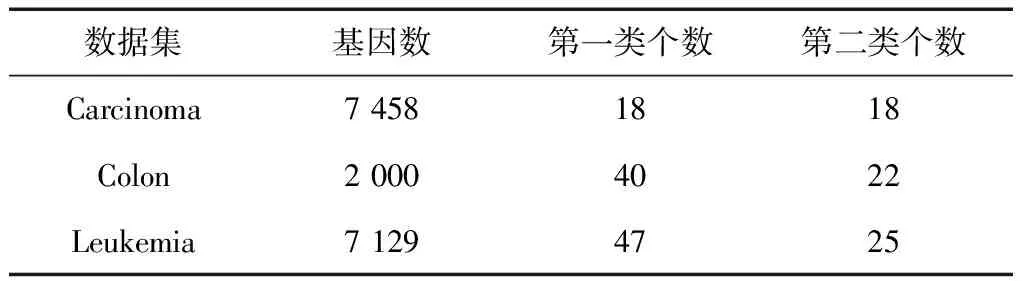
表1 基因数据性质

采用邻域来做特征提取的主要因素是邻域半径δ的选择，这里运用计算公式Std(ai)/λ，λ取0.5～1.5之间，步长为0.01，这样可以得到100组特征基因子集，通过十折交叉验证，采用SVM和KNN(K为3)计算分类识别率[12-14]。

实验环境采用Win7 64bit 操作系统，Intel(R)Core i7，8 GB内存，matlab R2017a。计算特征基因子集的分类识别率，得到基于固定邻域半径与优化邻域半径下的最高、最低、平均识别率及最高识别率下特征基因个数的平均值，如表2与表3所示。

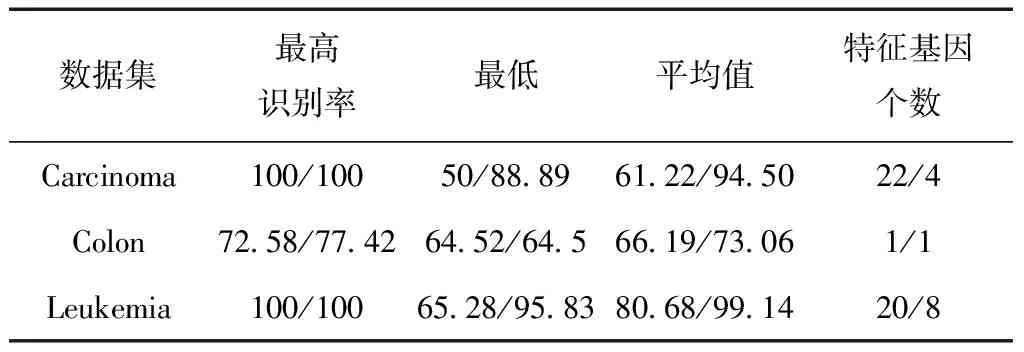
表2 基于固定/优化邻域半径SVM识别率 %

表3 基于固定/优化邻域半径KNN识别率 %

从表2、表3可以看出，Carcinoma与Leukemia最优识别率在两种分类器均可达100%，而Colon相对较差，SVM下固定邻域半径为72.58%，而优化邻域半径识别率达77.42%，在KNN分类器下分别为86.36%和81.82%。从平均识别率来看，基于优化的邻域半径在两种分类器下识别率均比固定邻域半径高，并且平均特征基因个数较少。

为了验证优化邻域半径粗糙集的有效性，本文引入3种典型的特征提取方法作为比较，分为主成分分析(PCA)、线性判别分析(LDA)及核主成分分析(KernelPCA)，特征基因数范围设定为2～10，得到3种数据集的分类识别率如表4、表5和表6所示。表中每列算法左边数据为SVM得到的识别率，右边为KNN得到的识别率。

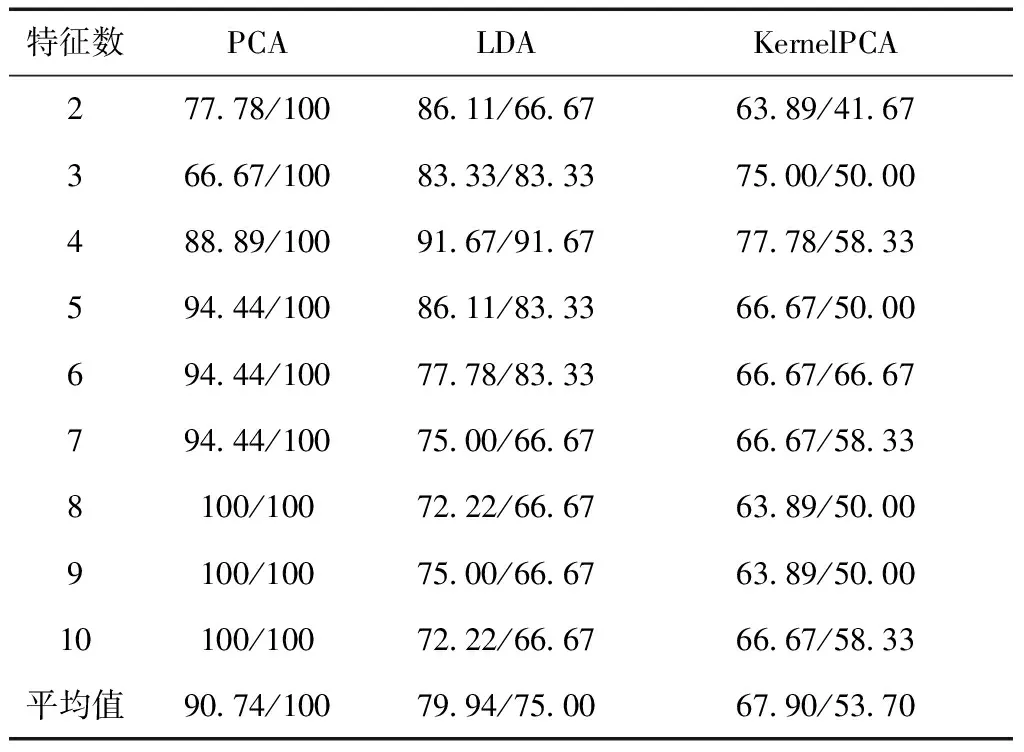
表4 Carcinoma数据集在3种降维算法下识别率 %

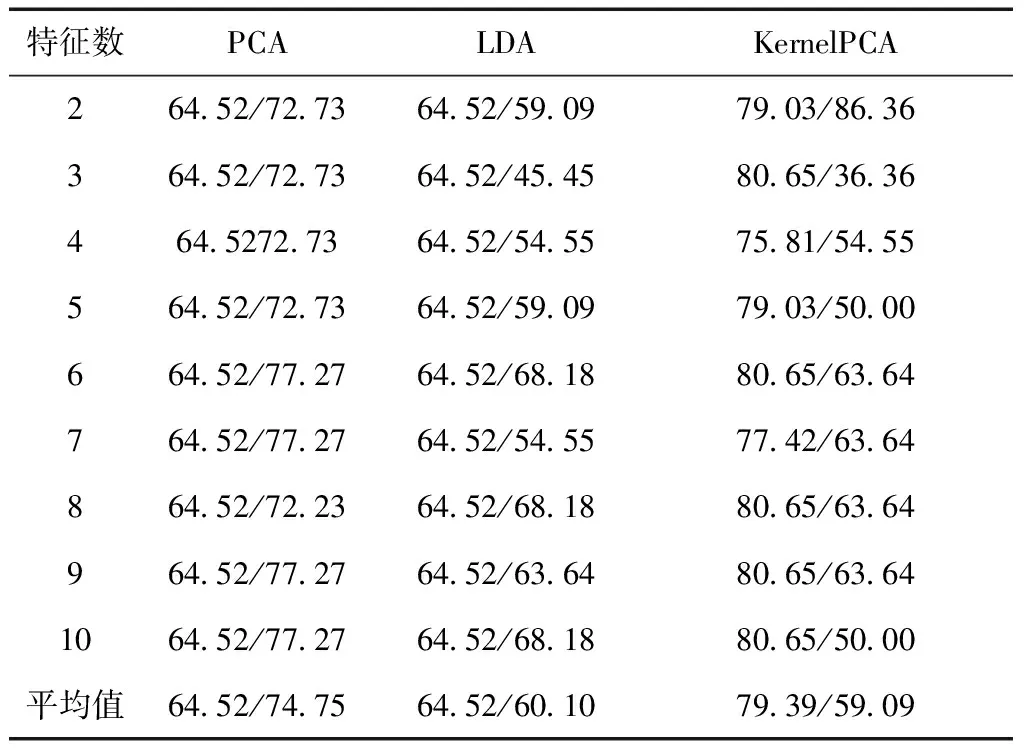
表5 Colon数据集在3种降维算法下识别率 %

从表中可以看出，Carcinoma数据集在用PCA特征提取后，两种分类算法识别率均达到最优识别率100%，而LDA和KernelPCA最优识别率SVM分类下分别只有91.67%和77.78%，KNN下为91.67%和66.67%。Colon数据集在PCA与LDA效果也不好，SVM最优识别率均为64.52%,KNN分别为77.27%与68.18%，而在KernelPCA则较高，为80.65%和86.36，Leukemia数据集在PCA与LDA效果也较好，SVM最优识别率分别为98.61%与93.06%，但还是低于基于邻域的特征提取，在KernelPCA效果则不明显，最优达73.61%。为了更好地比较5种算法在基因数据特征提取的优劣，比较识别率的平均值，并画出柱状图，如图2、图3所示。其中，优化邻域半径变化的标识为Var-Neighborhood，固定邻域的标识为Neighborhood。

表6 Leukemia数据集在3种降维算法下的识别率 %

图2 5种算法平均识别率(SVM)比较

图3 5种算法平均识别率(KNN)比较

从图2可以看出，基于优化邻域半径的特征提取在SVM分类器Carcinoma与Leukemia数据集识别率平均值均比其它4种算法好，而在Colon数据集中比PCA、LDA和固定邻域半径高，稍微低于KernelPCA，但两者也较接近。从图3可以看出，在KNN分类算法中，基于优化邻域半径在3种数据集的平均识别率都能高于或等于(只有与Carcinoma数据在PCA下相等)其他4种算法。

以上通过实验得出的结果，可以说明基于优化邻域粗糙集半径的约简算法在基因数据特征提取中能很好地应用，面对海量的高维数据，通过运用邻域约简算法提取特征基因，剔除无用或冗余基因，能达到更好的分类识别率[15-17]。

4 结束语

使用邻域粗糙集做属性约简算法进行数据的特征提取时，邻域半径的确定往往能影响最终的实验效果，绝大多数实验均使用事先已确定的邻域半径逐一搜寻最优的分类，本文对于这一问题，对邻域半径进行优化，提出使用计算各属性的标准差来得到一组邻域半径，再根据这组邻域半径计算各属性子集下的样本邻域。在Carcinoma、Colon与Leukemia数据集中实验，SVM与KNN分类结果均表明基于优化邻域半径得到的分类平均识别率均比固定邻域半径的属性约简算法高，并且和传统特征提取算法进行比较也高，这证明了改进邻域半径的有效性。

生物芯片数据是当前的研究热点之一，应用范围非常广，不断研究有效的算法，挖掘其中隐藏在芯片中有价值的知识[18-19]是当下面临的首要任务。