基于自适应虚拟阻抗的下垂控制策略研究

李 智，张 春，金 鹏，吕文齐

(安徽工程大学 电气工程学院,安徽 芜湖 241000)

微电网中的分布式电源(Distributed Generation,DG)一般通过电力电子逆变器与公共母线进行连接，大多采用下垂控制策略。下垂控制策略既可以实现系统负荷功率均分又可以在硬件上减少对有线通讯的依赖。但是下垂控制也有其局限性，其解决问题的工作条件是逆变器系统等效阻抗必须呈感性，但实际上，大多数的逆变器等效阻抗达不到此要求，因此，直接使用下垂控制策略会导致多逆变器并联输出无功功率分配不均和系统环流[1-2]。

文献[3-5]为解决系统输出电压降落过大这一问题，提出了改进的虚拟阻抗控制策略。通过引入虚拟阻抗来抵消一部分线路电阻，但是没有考虑到电压波动的问题，效果并不是很好。文献[6-7]提出动态虚拟阻抗的下垂控制策略，该策略虽能改善母线输出电压降落过大的问题，但是其无功功率分配精度在加入动态虚拟阻抗后明显下降。文献[8-10]提出了虚拟负电阻的控制策略来改善输出电压降落过大的问题，该策略虽能改善母线输出电压降落过大的问题，但其负阻抗取值对计算有着较高的要求，而且电网线路阻抗都不一样，很难估值，该方法在实际运用中难度较大。文献[11-13]提出了基于虚拟电容的下垂控制策略来改善系统无功均分和母线输出电压降落过大，但该方法精度较低，很难保证改善效果。

本文针对传统虚拟阻抗下垂控制工作时导致的输出电压降落过大的问题，提出基于自适应虚拟阻抗的下垂控制策略，通过把传统固定虚拟阻抗改成自适应虚拟阻抗，在不改变传统虚拟阻抗效果的基础上改善了输出电压降落过大问题。

1微电网逆变器并联系统分析

1.1 逆变器输出功率分配

设两参数完全相同的逆变器并联运行，根据等效定理得两逆变器并联运行的等效电路如图1所示。图1中U1，U2分别为两逆变器的输出电压，δ1，δ2分别为两逆变器的相位，I1，I2分别为两逆变器的输出电流，R1，R2分别为逆变器的等效输出阻抗和线路阻抗，X1为逆变器的等效输出阻抗，X2为逆变器线路阻抗，UL为公共母线的电压，δL为公共母线的相位，系统的负载电抗为ZL=RL+jXL。

图1 逆变器并联运行结构

一般情况下，公共母线上的相位可以忽略不计，令δL=0，由基尔霍夫定律可得，DGi(i=1,2)输出的有功功率和无功功率分别为

(1)

逆变器的功角基本都满足sinδi≈δi，cosδi≈1，通过计算可得传统下垂控制方程为

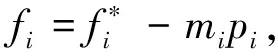
(2)

微电网系统在稳态运行时，由于频率的固定，因此，逆变器输出的有功功率能实现均分。系统等效输出的无功功率为

(3)

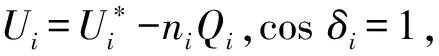
(4)

系统输出的无功功率相对偏差为

(5)

由式(5)可知，在传统下垂控制策略下，等效输出阻抗、无功下垂系数和电抗值的改变都会直接导致逆变器输出的无功功率偏差大小。但当负荷功率突然变化时，增大下垂系数只会增大母线输出电压与标准电压的电压差值，达不到标准要求，此时会对系统正常运行造成严重影响。

1.2 逆变器等效输出阻抗

传统下垂控制策略一般采用电压电流双闭环控制结构。为改善系统的动态响应速度，电流环采用比例控制器，为改善系统输出电压的无差跟踪能力，电压环采用比例积分控制器。基于虚拟阻抗的电压电流双闭环控制结构如图2所示。

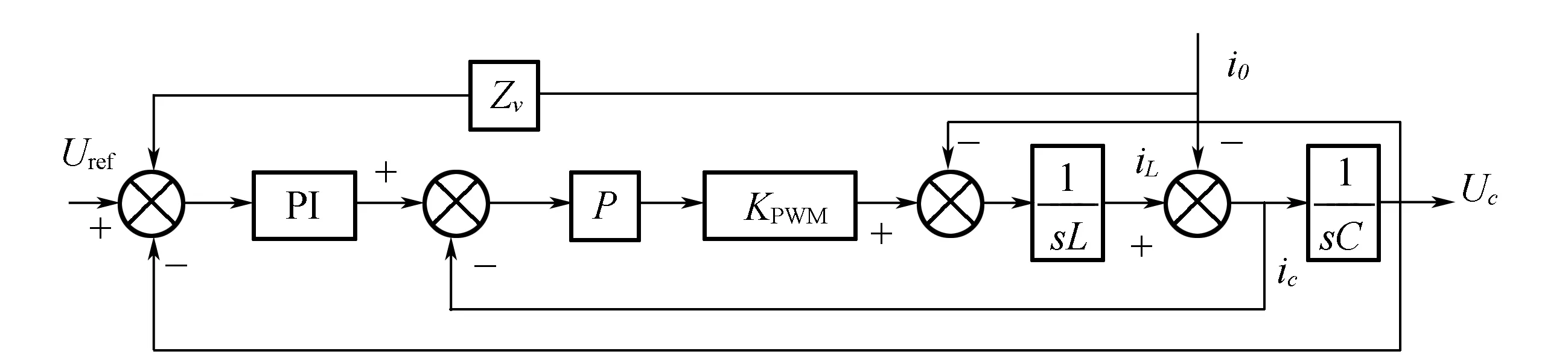
图2 基于虚拟阻抗的电压电流双环控制结构

图中，Uref为电压外环输入的参考电压；Kvp，KVi分别为电压外环回路PI环节的比例积分增益；电流内环回路的P环节增益为Kip；Kpwm为SPWM调制环节增益；iL为电感电流；ic为电容电流；io为负载电流；Uo为输出控制电压；Zv(s)为引入的虚拟阻抗。未加入虚拟阻抗的传递函数为

(6)

由图2可知，传统下垂控制逆变器等效输出阻抗为Zo(s)，Uo=UrefG(s)-Zo(s)io，令Uref=0，可得

(7)

其中：

(8)

由图2可知，加入虚拟阻抗后传递函数为

(9)

Zv(s)=Lvs，结合式(6)、式(7)可得加入虚拟阻抗后逆变器等效输出阻抗为

(10)

2 自适应虚拟阻抗控制策略

2.1 虚拟阻抗的无功均分与电压降落分析

根据式(4)可得基于虚拟阻抗的下垂控制策略的系统输出无功功率为

(11)

系统输出无功偏差为

(12)

故可得

(13)

由式(13)可知，基于虚拟阻抗的下垂控制策略能够有效地改善逆变器输出的无功功率偏差,减小无功环流。

设线路阻抗为Zline，则传统下垂控制策略下系统总电压降落为

ΔU=(Zo(s)+Zline(s))io.

(14)

基于虚拟阻抗的下垂控制系统总电压降落为

ΔU′=(Zo(s)+Zv(s)G(s)+Zline(s))io.

(15)

由分析可知，ΔU′>ΔU，则增加虚拟阻抗之后母线输出电压降落程度比传统下垂控制母线输出电压降落程度更大。

2.2 基于自适应虚拟阻抗的下垂控制策略

为改善母线输出电压降落过大的问题，本文提出自适应虚拟阻抗的解决办法。系统总电压降落如式(15)所示。参考式(15)，设自适应虚拟阻抗的值为

(16)

式中：ΔE为系统在微电网负荷侧测量的电压幅值与逆变器标准指令电压值间的差值；io(s)为负载电流。母线电压和电流在实时采集时，虚拟阻抗也会在自适应虚拟阻抗环的作用下，不断接受实时母线电压和电流值，实时计算出需要的阻抗值，并将计算出的合适的虚拟阻抗值代入到式(15)，此时可得到一个新的指令电压。

Uref1=Uref+ΔU1.

(17)

微电网在运行时，先赋值给微电网控制环节中的指令电压Uref1，然后实时检测出微电网负荷侧的母线电压，通过式(17)得到新的指令电压在微电网运行。

此时，随着逆变器输出电压的升高，系统的供电电压将稳定在正常范围。通过引入自适应虚拟阻抗，既改善了传统虚拟阻抗由于阻抗增大造成的电压降落问题，又进一步改善了虚拟阻抗无功分配精度，进而更好地提高了系统的供电质量。

3 仿真验证

搭建两DG并联运行的微电网系统，验证自适应虚拟阻抗下垂控制策略对改善系统无功均分、抑制系统环流和降低系统母线输出电压偏差的有效性。仿真电路如图1所示。在Matlab/Simulink环境下搭建相关的系统仿真模型，其主要参数如表1所示。

表1 仿真参数

设两DG并联运行，系统在0.3 s时增加公共母线上的负荷，0.6 s时断开该负荷，设仿真时间为0.8 s。仿真波形如图3、图4、图5、图6、图7所示。

图3为加入自适应虚拟阻抗前后2台逆变器频率波形，图3(a)为传统下垂控制系统频率波形，图3(b)为加入自适应虚拟阻抗系统频率波形。对比图3(a)、图3(b)可知，当逆变器输出阻抗呈阻感性时两DG在自适应虚拟阻抗的控制策略下，两DG加入负荷前后的输出频率相同，系统能更稳定地运行。对比可知，加入自适应虚拟阻抗后的下垂控制在频率调节时效果更好。

图3 系统频率波形

图4为加入自适应虚拟阻抗前后两DG输出有功功率仿真结果，图4(a)为传统下垂控制系统有功功率波形，图4(b)为加入自适应虚拟阻抗系统有功功率波形。对比图4(a)、图4(b)可知，在加入自适应虚拟阻抗之前，有功功率均分效果不好，进入稳态较慢，加入自适应虚拟阻抗后，有功功率实现均分，进入稳态较快。

图4 有功功率波形

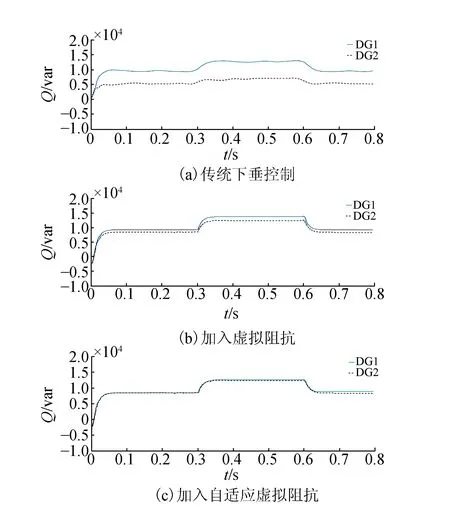
图5 无功功率波形

图5为加入自适应虚拟阻抗前后的无功功率仿真结果，图5(a)为传统下垂控制系统频率波形，图5(b)为加入虚拟阻抗系统无功功率波形，图5(c)为加入自适应虚拟阻抗系统无功功率波形。对比图5(a)、图5(b)、图5(c)可知，加入虚拟阻抗之前的两DG在0～0.3 s内，DG1输出无功功率为8.12 kvar、DG2输出的无功功率为3.97 kvar，两DG此时的无功分配偏差率为42.5%；在0.3～0.6 s期间，DG1输出无功功率为11.5 kvar、DG2输出无功功率为5.3 kvar，两DG此时的无功分配偏差率为45.6%，加入虚拟阻抗后两DG在0～0.3 s内，DG1输出无功功率为8.1 kvar、DG2输出的无功功率为6.2 kvar，两DG加入负荷前的无功分配偏差率为10.5%。在0.3～0.6 s加入负荷期间，DG1输出无功功率为10.28 kvar、DG2输出无功功率为9.34 kvar，两DG加入负荷后的无功分配偏差率为8.1%。加入自适应虚拟阻抗后，在0～0.3 s内，DG1输出无功功率为7.8 kvar、DG2输出的无功功率为7.2 kvar，两DG加入负荷前的无功分配偏差率为6.5%，在0.3～0.6 s加入负荷期间，DG1输出无功功率为10.32 kvar、DG2输出无功功率为9.36 kvar，两DG加入负荷后的无功分配偏差率为5.8%，对比可知，加入自适应虚拟阻抗对系统的无功功率均分改善更为明显。

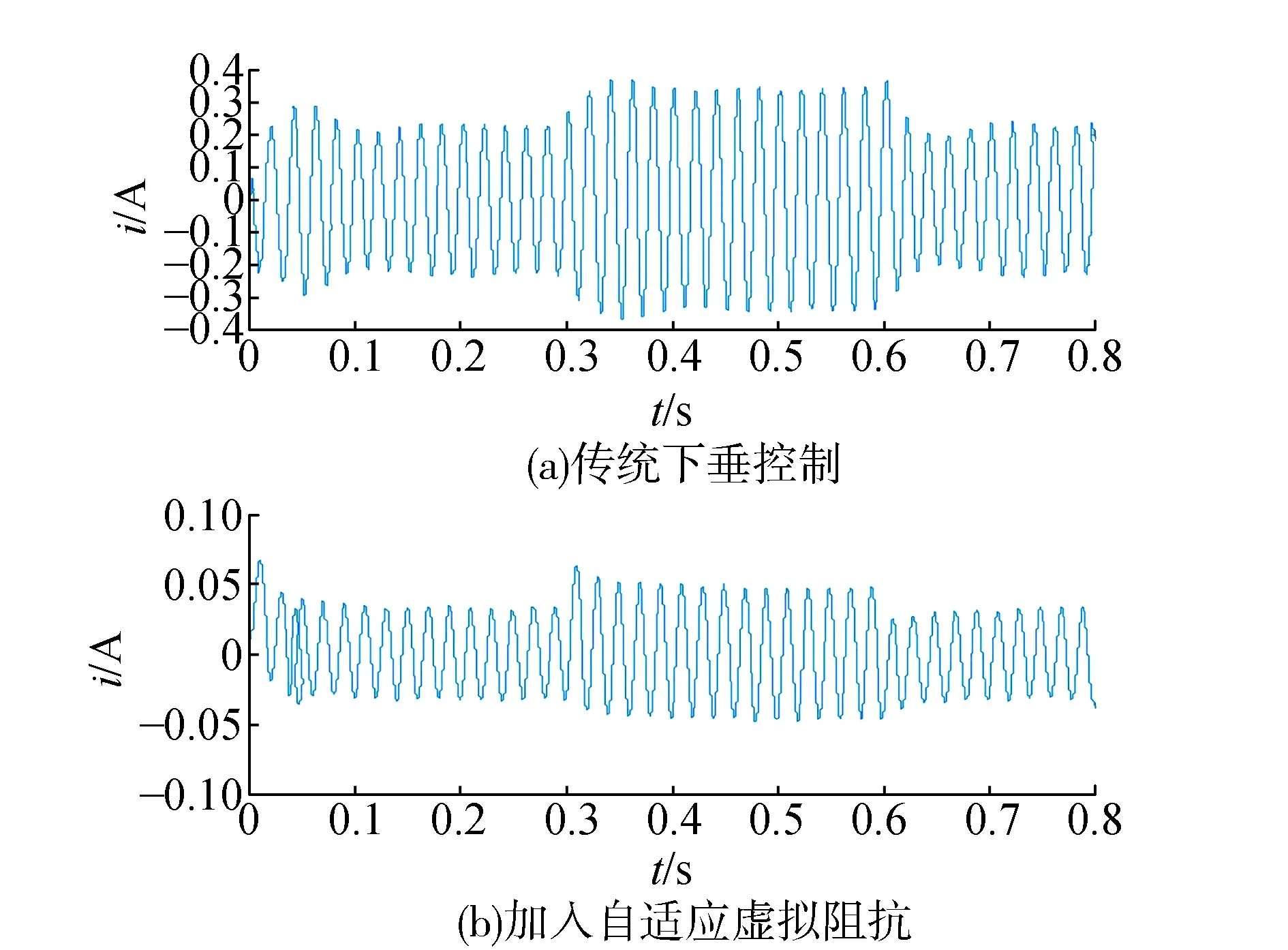
图6 系统环流波形

图6为2台逆变器加入虚拟阻抗前后系统环流仿真结果，图6(a)为传统下垂控制系统环流波形，图6(b)为加入自适应虚拟阻抗系统环流波形。对比图6(a)、图6(b)可知，传统下垂控制下的系统环流大约在0.2 A，加入自适应虚拟阻抗后系统的环流大约为0.05 A，对比可知，加入自适应虚拟阻抗后环流得到了很好地抑制。

图7 母线输出电压波形

图7为加入自适应虚拟阻抗前后逆变器输出电压仿真结果，图7(a)为传统下垂控制系统母线输出电压波形，图7(b)为加入虚拟阻抗后的系统母线输出电压波形，图7(c)为加入自适应虚拟阻抗系统母线输出电压波形。对比图7(a)、图7(b)、图7(c)可知，加入虚拟阻抗前，逆变器输出电压幅值约为295 V，系统给定的电压幅值为311 V，误差为16 V，加入虚拟阻抗后逆变器输出电压幅值约为290 V，与系统给定的电压幅值相差21 V，加入自适应虚拟阻抗后的电压幅值约为306 V，与系统给定的电压幅值相差5 V，可知，加入自适应虚拟阻抗对改善电压降落过大效果明显，为提高负荷供电电压质量提供了保障。

4 结束语

本文提出的自适应虚拟阻抗控制策略，在改善系统环流和无功分配不均问题的同时，通过虚拟阻抗的自适应调节，使虚拟阻抗值能够随着母线输出电压值实时在线调整，通过补偿输出电压指令值的方式来改善母线输出电压降落过大的问题，进而提高系统的稳态性能和电能质量。