形状记忆合金鼓包的挠度控制研究*

（南京航空航天大学航空学院机械结构力学及控制国家重点实验室，南京 210016）

激波控制鼓包（Shock Control Bump，SCB）是一种流动控制技术，在减小激波阻力的同时具有不附加黏性阻力的特点[1]。鼓包的外形极大影响减阻的效果，很多研究者根据飞行条件研究鼓包的最佳设计参数。Qin等[2]将鼓包分为三维和二维两种，三维鼓包边界全贴合于机翼表面，二维鼓包是部分贴合，比较了两者的减阻效果。李沛峰等[3]利用CFD 仿真计算，系统阐述了鼓包的位置、高度和长度对激波弱化的影响。

但是固定式鼓包的设计参数，如高度、位置等固定，在无激波阻力时鼓包会破坏机翼原有的设计结构，反而会增加飞行阻力。Jlinks 等[4]设计了一种可变挠度的鼓包，采用一块0.6mm 厚的铝制薄板，利用80N 的力驱动器可以产生13mm 的挠度行程，而且可以随时根据飞行条件进行挠度的优化。聂瑞等[5]提出了形状记忆合金（Shape Memory Alloy，SMA）鼓包，通过仿真研究，鼓包升温时挠度变大，降温时挠度变小，在相变过程中的挠度变化可达长度的4%。温度驱动式的鼓包相比于力驱动的鼓包，驱动器设计更为容易，但是在温差过大时耗能会很严重。在飞行器巡航过程中一般环境温度可达–50℃，如果利用环境温度使鼓包为凸起状态，而仅在起飞和降落过程中加热鼓包使其变平则可以大大减少耗能。因此，一个升温挠度变小、降温挠度变大的鼓包更加符合实际应用。

SMA 的驱动控制一般采用闭环控制，其反馈量一般有温度、位移、电阻3 种。电阻反馈一般用在小型的嵌入式驱动器中，以便于系统的集成[6]。对驱动位置的控制精度要求高时，可采用位移反馈[7]。由于丝的精确温度获取不易，采用温度反馈不多见，但对加热速率关心的控制可采用温度反馈[8]。SMA 的控制策略一般分为有模型控制和无模型控制。无模型控制一般是利用PID 控制或结合智能控制的PID 联合控制。Ahn等[9]结合模糊控制和PID 控制策略，用试验证明了其可以成功地进行SMA 丝的位置控制，且效果较单独的PID 控制更好。Ahola 等[10]将抗饱和PI 控制与神经网络控制进行比较，两种方法各有优缺点。有模型控制即先对SMA 丝的温度–位移迟滞效应进行建模，常采用Preisach 模型[11]和Prandtl-Ishlinskii（PI）模型[7]两种，然后根据逆模型进行控制。有模型控制和无模型控制都可以进行稳态控制，需要快速跟踪控制时适合采用有模型控制，无模型控制的优点在于控制算法较为简单，适合在计算资源不丰富的情况下使用。

驱动器中使用的多为SMA 丝，可以通过电流来加热，响应速度快，且散热容易。SMA 鼓包是板状材料，只能采用接触式和辐射式的加热方式，驱动速度慢，相变导致的宏观位移变化也比较复杂，因此板状SMA 的驱动控制研究较少。SMA 丝作为驱动器一般需要设计额外的传动装置，SMA 鼓包则不需要，SMA 鼓包的优点是一体性好，因此对其进行驱动控制研究也有重要的意义。

本文针对具有双程记忆效应的SMA 鼓包，建立了温度–挠度的迟滞模型，并用试验验证了应用该模型可以提高挠度的控制效果，为SMA 鼓包的驱动控制提供了一种思路，同时也为验证SMA 鼓包可以应用在SCB上打下了基础。

1 SMA 鼓包简介

SMA 鼓包的材料是Ni50.1Ti49.9，半径60mm，厚度0.55mm，变形区的半径为40mm。经过训练可获得双程记忆效应，即在通过施加压力使鼓包产生弯曲，再进行高低温循环数10 次，如图1所示。

关于训练的详细说明可参考文献[12]。将训练好的鼓包安装在平台上，凸起的面朝上，如图2所示。以鼓包在–20℃时的中心点位置为零参考点，在外界环境温度不变、不施加外载荷的条件下，鼓包的温度和中心点挠度的关系如图3所示，可回复位移约为1.2mm，占鼓包长度的1.5%。图3中曲线的Ⅰ～Ⅱ段和Ⅲ～Ⅳ段是鼓包的相变阶段，0～I 段和II～III 段是鼓包的热膨胀阶段，相变温度分别为As=50℃，Af=120℃，Ms=62℃，Mf=5℃。

鼓包在真实的应用环境中会承受外加载荷并受到环境温度的影响。非均匀温度场会改变鼓包在升降温过程中的挠曲线，但不影响鼓包的最大变形能力[13]。随着鼓包表面压强的增加，鼓包的变形性能会逐渐衰减。对于一个0.55mm 厚度的SMA 鼓包，在鼓包的上表面承受4000Pa 压强时，鼓包的最大变形能力会衰减12.5%，衰减之后的变形能力依然可以满足激波控制的要求[13]。

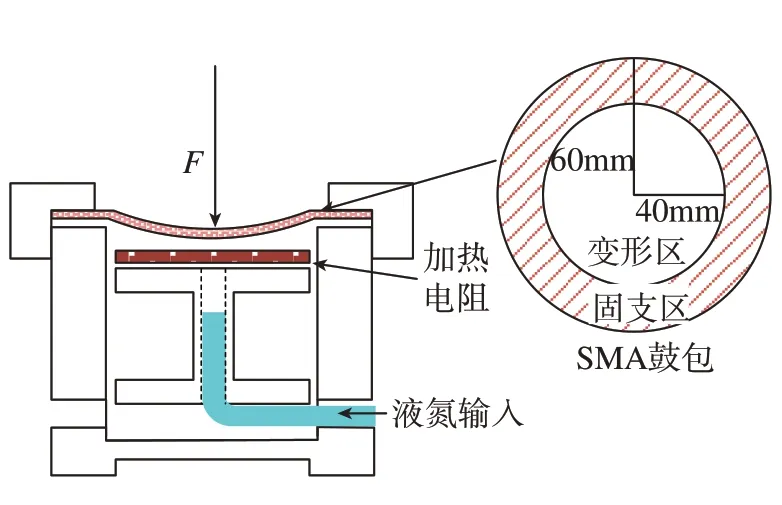
图1 SMA鼓包训练示意图Fig.1 Training diagram of SMA bump

图2 SMA鼓包的安装Fig.2 Installation of SMA bump

图3 SMA鼓包中心点挠度与温度的关系Fig.3 Relationship between temperature and deflection of center point of bump

2 SMA 鼓包的迟滞模型

迟滞现象是指系统输出不仅与当前的系统输入有关，而且与系统的历史输入极值有关的一类现象。具体表现为体统的输入与输出并非一一映射关系。在SMA鼓包中，迟滞现象即表现为温度与挠度之间的多映射关系，如图3所示。

2.1 Preisach理论

Preisach 模型常被用来描述压电[14]、SMA 材料[15]的迟滞行为。Preisach 模型由一系列连续的双稳态单元组成，如图4所示。γαβ是一个基本的迟滞算子，可由矩形状的环表示，α和β分别表示输入的上下切换值，即表示一个双稳态，当输入值大于α时，γαβ值为1，当输入值小于β时，γαβ值为0。数学表达式可以写作：

式中，μ（α，β）表示密度函数；u（t）表示输入量。

假设一个系统的输入量从0 开始变化，其Preisach模型的几何解释如图5所示。

三角形表示Preisach 平面，γαβ和（α，β）在三角形内具有一一对应关系，密度函数μ（α，β）在内部为非负函数，在外部取0。当输入量增加到α1时，其对应的Preisach 平面以α=α1为分界线，S+表示γαβ为1，S–表示γαβ为0。当输入量下降到β1时，会产生一条竖直方向的分界线β=β1，此时S+的面积会缩小。当输入量增大到α2时，此时的分割线为α=α2。由此可发现规律，即输入量上升时会产生水平分割线，下降时会产生竖直分割线。由此可得，在任意一个瞬时，输出表达式可以写作：

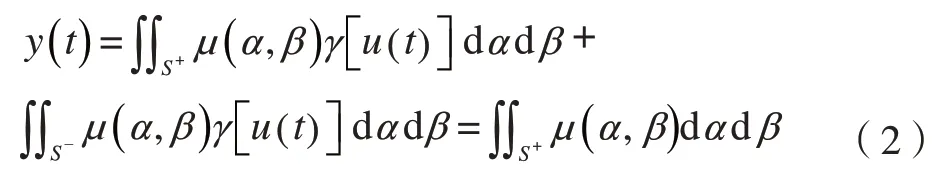
式（2）表明，Preisach 模型的输出与三角形S+的动态划分有关，即与输入量的极值有关。

2.2 数值实现

由于式（1）的Preisach 模型是一个双积分式，其中基本算子的数量是无限的，为了节省计算资源和满足实时控制的需求，一般要进行离散处理。文献[16]提供了一种思路，首先定义等价函数：

式中，yα是输入量为α时的输出；yαβ是输入量由α单调下降到β时的输出，又称一次下降曲线。

由图5中的（b）可得，密度函数在S+区域的积分就是输入量为α1和β1时的输出差值。即：

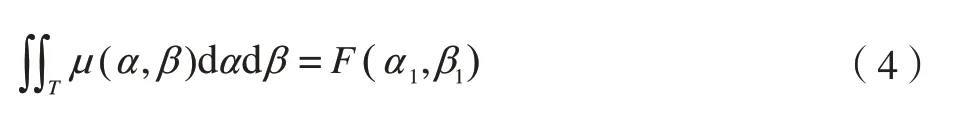
图6是一个典型的输入变化时的S+区域的动态划分，其中图6（a）表示输入最终减小为某一个值u（t），图6（b）表示输入最终增加到某一个值u（t）。S+可以由一系列的Qk组成，表达式可以写作：

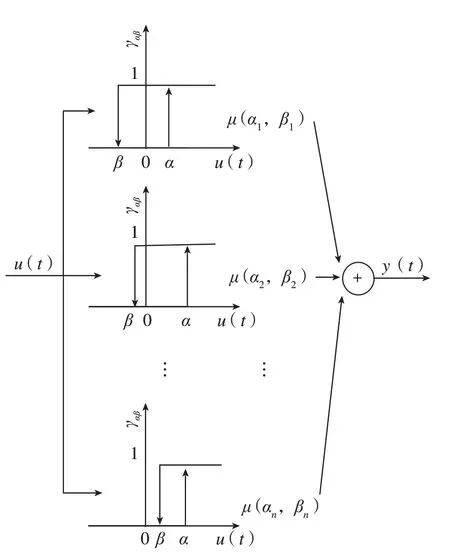
图4 Preisach 模型原理Fig.4 Principle of Preisach model

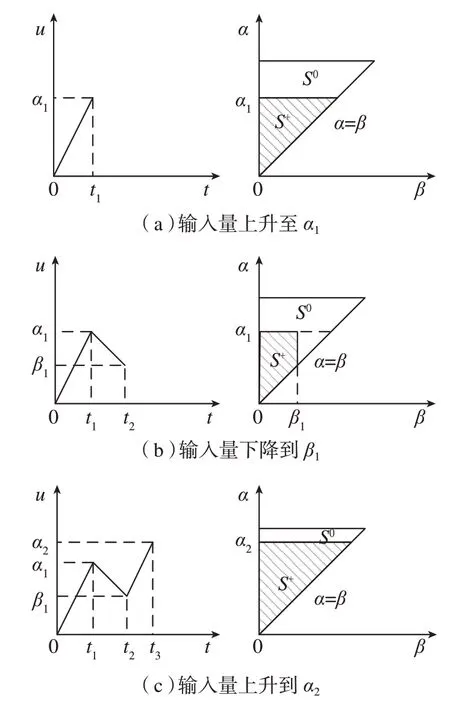
图5 Preisach模型的几何解释Fig.5 Geometric interpretation of Preisach model

Qk面积即可以表示为T（Mk，mk–1）和T（Mk，mk）面积之差：

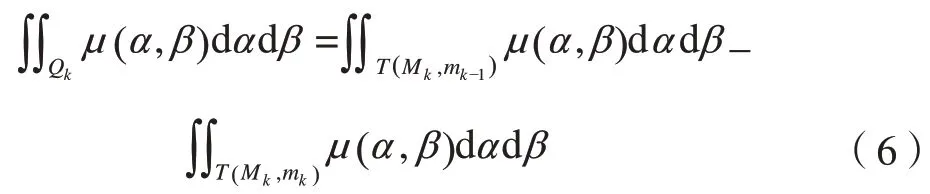
又因为：

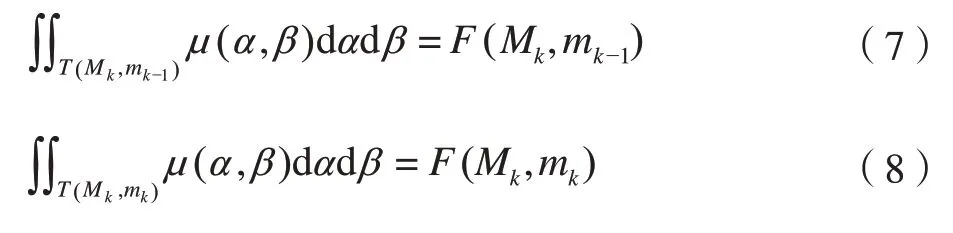
由式（6）、（7）、（8）可得：

由式（2）、（5）、（9）可得：

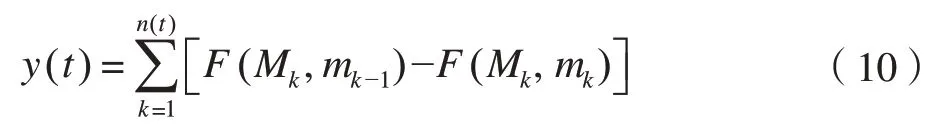
由图6（a）可得，当输入量最终增加至某一个值u（t）时，有mn=u（t），式（10）可以写作：

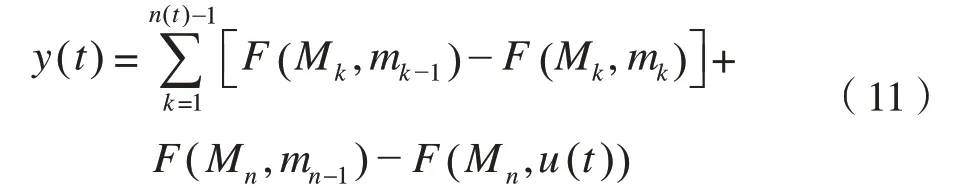
若输入量最终减小到某一个值u（t）时，有Mn=mn=u（t），式（10）可以写作：

由以上分析得，可以用一系列离散的的一次下降曲线来近似表示系统的输出。

2.3 模型辨识

通过2.2 节的讨论，将一节下降曲线中的端点温度离散处理，用试验的方式可获取各个离散温度下的一次下降曲线[17]。对Preisach 平面进行以下网格的划分：

则一共为110 个网格点，排除α、β的35 个网格点，实际需要测量75 组数据。设鼓包在马氏体相变结束温度以下为负饱和状态，在奥氏体相变结束温度以上为正饱和状态。从负饱和状态开始升温，分别测量每个离散温度对应的格点上的F（α，β），通过MATLAB 中的线性插值将网格点细分，每1℃设置一个网格点，可以得到Preisach 平面，如图7所示。

3 SMA 鼓包的挠度控制系统设计

3.1 PID控制

PID 控制是一种线性控制方法，它根据目标值r（t）和实际输出值y（t）构成控制偏差e（t），即e（t）=r（t）–y（t），对偏差e（t）进行比例、积分、微分运算，将3 种运算结果相加，得到控制输入u（t）。图8是PID 控制的原理。

PID 控制在连续时间域的表达式为：

式中，kp为比例系数；Ti为积分时间常数；Td为微分时间常数。

数字控制系统是一种采样控制，只能根据采样时刻的偏差值计算控制量，因此式（14）不能直接用于数字控制系统，需要进行离散处理。以一系列的kT（T为周期）代表连续时间t，可近似得到以下用于实时数字控制系统的离散化的PID 表达式：

图6 Preisach模型的动态划分Fig.6 Dynamic division of Preisach model

图7 插值得到的Preisach平面Fig.7 Interpolated plane of Preisach

图8 PID控制原理Fig.8 Principle of PID control

式中，kp为比例系数；ki为积分系数，ki=kp/Ti；kd为微分系数，kd=kpTd；u（k）为第k次采样时控制器输出；e（k）为第k次采样时刻输入控制系统的偏差值；e（k–1）为第k–1 次采样时刻输入控制系统的偏差值；T为采样周期。

3.2 控制系统设计

图9是控制流程的示意图。

利用PXI 系统搭建了控制平台，全部的试验装置及连接如图10所示。

传感器使用热电偶采集温度，激光位移传感器采集位移，两者通过相应的采集卡将信号传输给控制器。控制器是一台计算机，在其上运行LABVIEW 软件，对采集的数据进行PID 计算并输出相应控制量，一路通过PID 计算得到u1信号控制加热，另一路通过开关量u2控制冷却。驱动器分为加热驱动器和冷却驱动器，分别采用两根电阻加热棒辐射加热和液氮喷气冷却。利用采集卡PXIE–4300 采集位移信号，PXIE–4353采集温度信号，其中参与PID 反馈运算的是位移信号，NI–9264 是用来输出两路控制的信号。

鼓包的LABVIEW 程序中温度误差和位移误差同时参与PID 计算，只有两类误差均为0，才会停止输出控制量，防止当位移误差不再变化时，温度变化导致热膨胀产生。图11是三维鼓包的LABVIEW 控制程序的结构。

4 试验结果

控制试验仅针对在外界温度保持不变（30℃）、鼓包不承受外加气动载荷的条件下进行。设此时的挠度值为0，根据图7的Preisach 平面，按照极值点尽量少的准则，可根据目标位置确定温度变化的过程，如表1所示。图12是Preisach 平面的动态划分。

利用Z–N 整定法确定PID 参数，在试验中记录挠度和温度数据，挠度和温度数据分别如图13和14 所示。

图15展示了控制过程中挠度和温度的关系。阶段4 的曲线较其他3 个阶段不平缓，这是由于鼓包表面的冰霜的凝结与消融过程所导致。

当不考虑温度与挠度之间的关系时，可利用挠度反馈的PID 控制进行试验，图16比较了无模型控制和有模型控制的效果，有模型控制的稳态误差和超调量均有不同程度的减小。

表2展示了有模型控制和无模型控制过程中的部分时域性能指标，其中有模型控制的最大相对误差为第4 阶段的5.17%，无模型控制的最大相对误差为第4 阶段的7.33%。

图9 控制系统的流程图Fig.9 Flow chart of control system

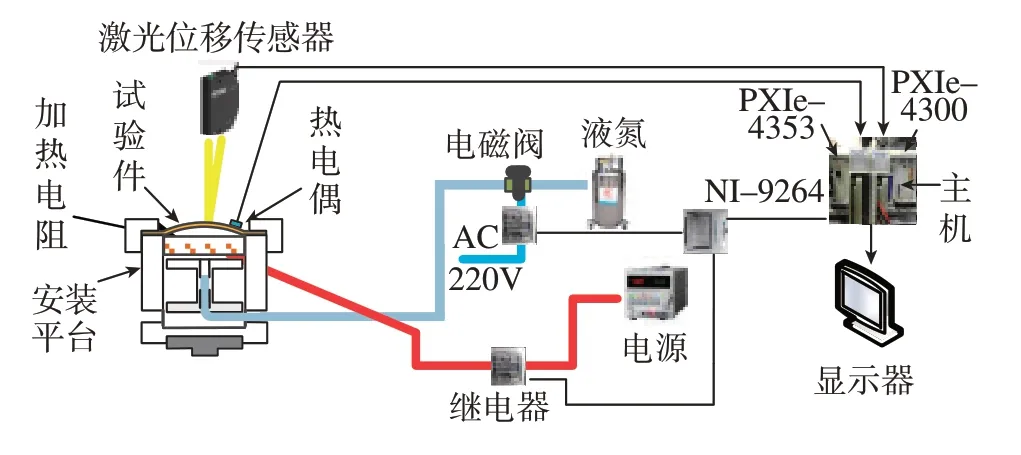
图10 试验仪器Fig.10 Experimental apparatus

图11 LABVIEW程序结构Fig.11 Program structure of LABVIEW

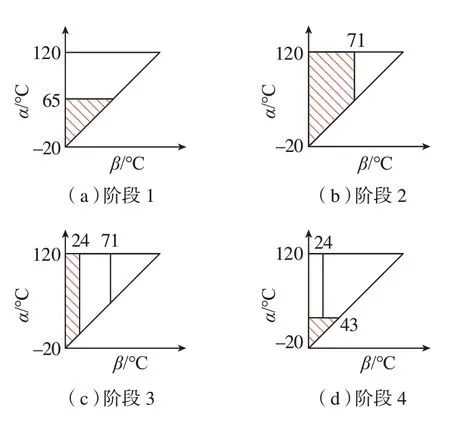
图12 控制目标的Preisach平面动态划分Fig.12 Dynamic division of Preisach planes for control targets

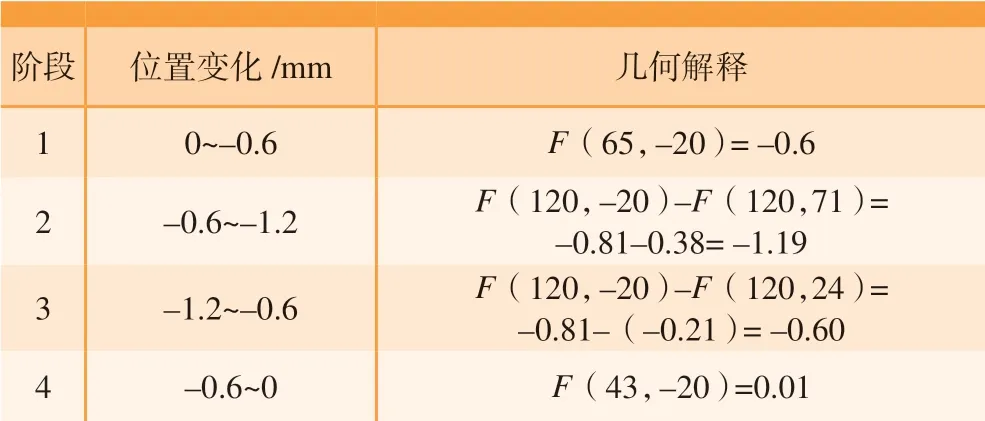
表1 控制目标Table1 Control targets

图13 挠度随时间的变化Fig.13 Deflection change over time

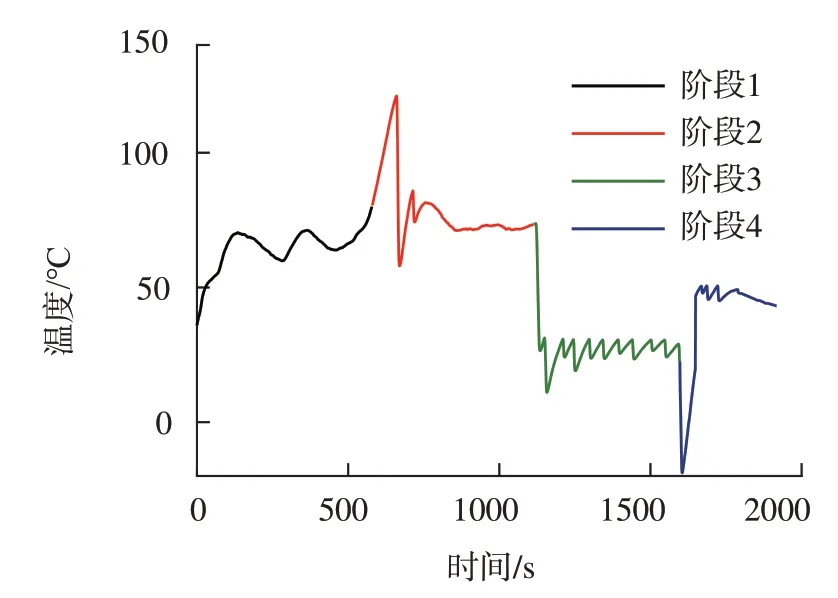
图14 温度随时间变化Fig.14 Temperature change over time

图15 挠度与温度的关系Fig.15 Deflection vs temperature

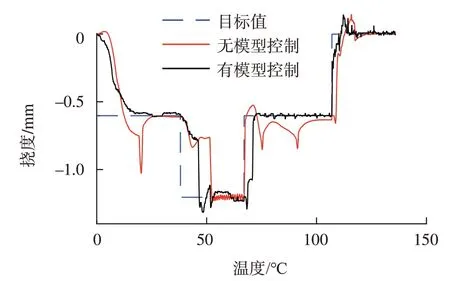
图16 有模型和无模型控制对比Fig.16 Comparison of control with and without a model

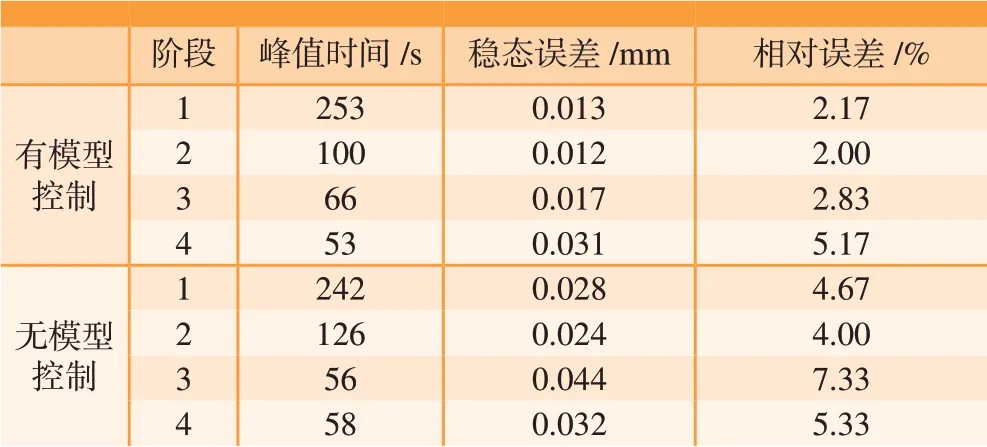
表2 时域性能指标Table2 Time domain performance index

5 结论

本文以被动式的激波控制鼓包为应用背景，提出了具有双程记忆效应的SMA 鼓包，并在不承受外加气动载荷的室温环境下对其进行了挠度控制，研究表明：

（1）经过训练后的具有双程记忆效应的SMA鼓包，可实现通过控制温度以改变挠度，可恢复变形达到鼓包长度的1.5%；

（2）利用Preisach 模型可以建立SMA 鼓包温度—挠度的迟滞模型，得到目标挠度和目标温度的对应关系；

（3）在迟滞模型的基础上，利用挠度和温度的双目标PID 控制可以对鼓包的挠度进行精确控制，且比无模型的单目标PID 控制效果更好。