基于多线性稀疏主成分的高光谱影像特征提取

陈志超,张正,刘昌华 ,周亚文,芦俊俊,王春阳

(1.河南理工大学 测绘与国土信息工程学院，河南 焦作 454000；2.北京吉威时代软件股份有限公司，北京 100194)

0 引 言

高光谱遥感影像包含几十甚至几百个窄波段形成的连续光谱波段，光谱范围可覆盖紫外、可见光、近红外乃至热红外[1-2]。通过获取不同地物超高分辨率的光谱信息，高光谱遥感可实现对地面目标的精细描述，其“图谱合一”的成像方式将影像空间结构信息与光谱信息结合在一起，大大提高了人类对地全方位探测的能力，以及对观测对象的理解和认识[3]。高光谱遥感影像成百上千的波段在带来丰富光谱信息的同时，也出现了大量冗余信息以及数据传输和存储困难。高光谱影像应用中不同波段均具有不同贡献值，有些波段甚至没有贡献值，将高维空间中的数据通过线性或非线性映射投影到低维空间中，找出隐蔽在高维观测数据中有意义且能揭示数据本质的低维子结构，可以避免高维数据的维数灾难问题，从而有效促进高维数据的分类、反演等应用[4]。在综合分析张量空间和影像稀疏特性优势的基础上，针对以往特征提取算法均基于向量对高光谱影像进行处理,没有利用高光谱影像的立方体空间结构信息这一缺点，本文提出基于多线性稀疏主成分分析(MSPCA)的高光谱遥感影像特征提取算法，并利用中国嘉兴典型村庄和美国内华达州Curprite矿区的高光谱影像数据进行分类试验，以验证所提算法的有效性。

1 遥感数据来源与处理

1.1 遥感数据来源

本文分别选取AVIRIS光谱仪获取的美国内华达州Curprite矿区高光谱影像和AISA获取的我国浙江嘉兴地区高光谱影像进行试验。

浙江省嘉兴市典型村庄利用AISA获取的高光谱影像，光谱380～2 500 nm，影像大小525像素×356像素，原始数据共126个波段。遥感影像中包含植被1(树木)、植被2、土路、水泥路、房屋、水体6种地物，由波段95，64和33组成的假彩色影像和地面参照数据如图1(a)和(b)所示。

图1 嘉兴地区高光谱影像

美国内华达州Curprite矿区高光谱遥感数据是由机载可见光/近红外成像光谱仪(AVIRIS)获取，光谱400～2 500 nm，光谱分辨率约10 nm，影像大小500像素×320像素，原始数据共有224个波段，但是有一些波段受噪声干扰和水蒸气吸收影响严重，去除这些受影响严重的波段后，用余下190个波段进行试验。遥感影像中包含伊利石、地开石、凝灰岩、干盐湖、石英石、高岭石、水铵长石、明矾石等8种矿物，由波段178，111和33组成的假彩色影像和地面参照数据如图2(a)和(b)所示。

图2 内华达州高光谱影像

1.2 遥感数据预处理

浙江省嘉兴市典型村庄遥感数据为自主拍摄获取的影像，由于所使用AISA传感器获取数据的数据格式本身就与其他数据格式存在差异，加上拍摄过程中造成的几何畸变，因此，在降维试验之前首先需要对影像进行预处理。本文使用的AISA数据所进行的几何校正属于已知几何信息的几何校正这一范畴，具体预处理步骤：TIF影像左右翻转；查找表文件(geographic lookup table，GLT)地理位置的生成；利用GLT文件几何校正影像；输出降维试验中使用影像。从图3可以看出，嘉兴地区几何校正前后存在影像角度和地物位置等多个变化。

图3 嘉兴地区几何校正前后影像

2 研究方法

2.1 张量空间下的高光谱影像特征提取算法

高光谱影像特征提取旨在降低数据维数，消除“维数灾难”现象并且减弱由于样本有限导致的建模不准确等问题，从而有效提高高光谱影像反演、分类等应用的效率和精度[5]。随着高光谱特征提取技术的不断发展，以数据立方体结构为主的数据分析方法逐渐受到重视。张量是在向量与矩阵基础上的推广(最早由William Ron Hamilton在1846年引入到数学中)，众多学者开始研究张量空间的高光谱遥感影像特征提取方法。YAN S等[6-7]将线性判别分析(linear discriminant analysis，LDA)推广到高阶张量空间中，提出多线性判别分析(multilinear discriminant analysis，MDA)即张量表示的判别分析(discriminant analysis with tensor representation，DATER)，但MDA变量无法收敛且受参数影响较大，也就是说YAN S等[6]的算法不能全面而系统地确定子空间维度。由于张量对象的子空间维数可能非常高,致使穷举法确定参数不可行。LU H等[8]将主成分分析[9](principal component analysis，PCA)推广到任意高阶张量空间中，提出多线性判别分析(multilinear principal component analysis，MPCA)。MPCA是PCA的拓展，MPCA的目的是获取一个多线性转换(或投影)集。PCA是将向量投影到低维向量，而MPCA是将张量投影到低维张量，最终在低维子张量上进行分类或其他应用。模式识别或机器视觉应用中的典型张量对象通常为指定的高维张量空间，高维空间数据复杂、计算量大且样本相对稀少。然而，由于张量对象与周围对象具有强相关性，因此,可以假设张量空间高度约束在本质低维的流形子空间中，其优势在于能够直接将多维张量形式数据投影到低维张量子空间，而不改变影像数据的空间结构，并在此基础上解决高维小样本问题并提高计算速度和处理效率。但是，由于高光谱影像中复杂多样的地物类型以及样本分布的不规范，若不考虑数据本身的稀疏结构，特征提取就不具备合理性；而稀疏表示利用感兴趣信号的稀疏性和海量高维数据的高冗余性，可有效提取高光谱遥感影像的地物特征信息，是一种新型的数据表达方式[10]，该数据表达方式已成功应用在高光谱影像空-谱数据融合、混合像元分解、超分辨率重建和去噪等方面。因此，本文将稀疏表示引入到MPCA中，提出多线性稀疏主成分分析(multilinear sparse principal component analysis，MSPCA)，进行高光谱遥感影像的特征处理，同时利用稀疏与张量学习的优势以期得到更高精度的分类效果。

2.2 多线性稀疏主成分分析模型的建立

相关研究表明[6-11]，当一维的方法扩展到高阶张量时，相应的扩展方法通常优于原始方法，尤其是在小样本的情况下。其次，引入稀疏特征选择的L1范数可以提高投影精度、增强泛化能力和分类鲁棒性[12-14]。将PCA扩展到更高阶张量形式(MPCA)后，引入用于稀疏特征选择的L1范数，可以进一步改进算法(即MSPCA)性能。本文的多线学习方法受到L1规范施加的稀疏约束。MSPCA在所有张量模式中执行稀疏降维，并且捕获原始张量的大部分变量。

假设训练样本被表示为n阶张量，其中N为训练样本的总数。根据对于任意给定模式k下多线性回归问题与MPCA的目标函数之间的密切关系[15]，为了获得多线性稀疏主分量，lasso[16](一种补偿最小二乘方法，在L1范数的基础上增加一个约束)被强加于MPCA标准模式k扁率的回归表示上。MSPCA目标函数为

(1)

其中，βk，j≥0作为约束优化处理的惩罚系数，用于惩罚不同主成分向量的荷载。当βk，j=0时为MPCA算法，因此，在MSPCA中假设βk，j>0。

MSPCA的操作步骤如下。

输入：张量样本{Xi∈Rm1×m2×…×mn，i=1，2，…，N}，迭代次数Tmax，低维维度di(≤mi)，i=1，2，…，n。

输出：多线性稀疏子空间U1，U2，…，Un(i=1，2，…，N)。

第一步：中心化输入的训练样本。

第三步：对于t=1:Tmax

对于k=1:n

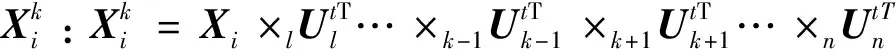
解决弹性网问题：

结束

结束

第四步：输出多线性稀疏子空间U1，U2，…，Un(i=1，2，…，n)。

下面介绍MSPCA的解法，公式(1)可得

(2)

可见，如果Bk已知，式(2)与下面弹性网问题的解相同

j=1，…，m′k;

(3)

另一方面，有

当Uk固定且已知时，式(4)中第1,3,4项为常数，可写为

(5)

根据文献[17]，对于给定Uk，上述最大化问题的最优解为

(6)

为简便起见，假设m1=m2=…=mn=m且训练样本N的总数与特征维度mn相当，MSPCA的复杂度为tO(n2Nmn+1+nNmn+1+nTm3)，其中t为迭代次数，T为弹性网的迭代次数。虽然形式复杂，但弹性网在一个很低的维度上能很快收敛，且整体迭代次数通常不会太大。在相同的迭代次数下，MSPCA显然比MPCA和SPCA更复杂。然而，计算稀疏主成分向量只是在模式识别任务的训练阶段才需要，因此，这一不足可以被忽略。

2.3 试验参数设置

选取3种特征提取方法进行对比试验，以验证本文所提方法的有效性，选取对比的特征提取算法包括PCA，SPCA和MPCA。在监督特征提取和影像分类中，随机选择每类地物样本中50个作为训练样本，剩余的样本作为验证样本。为增加试验的可比性，所有特征提取方法设置特征提取后的维数为C-1(C为样本类别个数)。

2.4 基于SVM的遥感分类及精度评价方法

选用支持向量机(support vector machine，SVM)[18]分类器相结合对高光谱影像进行分类，并与其他PCA特征提取方法进行对比分析。使用Kappa系数、平均精度(average accuracy，AA)和总体精度(overall accuracy，OA)作为分类评价指标。为了提高试验的可靠性和准确性，本文对SVM分类中核函数参数和规则化系数分别在{2-10，…，210}，{2-5，…，210}的范围内选择最优[19]，并使用一对余(OAR)的策略进行分类。而且每种算法进行10次重复分类试验，最后选取10次重复分类试验的平均值为最终结果。

3 结果与讨论

3.1 嘉兴地区典型村庄试验结果及讨论

表1为在不同算法下嘉兴地区影像中各类地物的分类精度OA，AA和Kappa系数，其中Kappa系数和OA为10次试验的平均值。从表1可以看出，相比其他算法，MSPCA分类精度均较高，尤其是水体分类精度达到了85.81%，而基于原始波段特征分类精度仅为64.16%；总体精度OA达到96.36%，平均精度AA达到95.02%，Kappa系数达到92.33%，均优于其他算法精度。在图4的分类图中也可以看出,MSPCA降维算法错分点更少，地物分布更加平滑。

图4为原始影像及各特征提取方法对应的分类结果图，从图4可以看出，对于本文提出的MSPCA方法，分类图中的类别噪声最少，空间连续性得到有效的增强。

表1 嘉兴地区影像中各类地物在不同算法下的分类精度

图4 各算法在嘉兴地区数据集上的分类结果

Fig.4 Classification results of each algorithm of the data set of Jiaxing area

3.2 内华达州Curprite矿区试验结果及分析

在Curprite矿区数据集中，使用与嘉兴市典型村庄数据集相同的参数设置方法，在不同特征提取方法下各类地物的分类精度OA，AA和Kappa系数如表2所示，对应的分类图如图5所示。由表2可知，MSPCA方法对大部分地物的分类精度、总体分类精度、平均分类精度和Kappa系数要明显优于其他算法，这表明在高光谱影像特征提取过程中，MSPCA算法能提取出更为有效的特征。表2和图5显示MAPCA在分类图中错分点更少，地物分布更加平滑，进一步验证了本文所提特征提取算法的有效性。

4 结 论

(1)基于张量学习的优势和稀疏特性的问题，提出多线性稀疏主成分分析模型，进而提出MSPCA高光谱遥感影像特征提取方法。

(2)两组试验的分类精度均较高，其中MSPCA的特征提取算法精度的OA，AA和Kappa系数均为最高值，特别是嘉兴市典型村庄遥感影像中的水体和Curprite矿区遥感影像中凝灰岩等弱特征地物的分类精度得到了大幅提高。

表2 Curprite矿区影像中各类地物在不同算法下的分类精度

图5 各算法在Curprite矿区数据集上的分类结果

(3)在综合考虑影像稀疏特性和张量空间算法优势的基础上，MSPCA降维算法有效提高了影像分类精度，为较难分类的弱特征地物分类与反演提供了新的方法。