基于Mallat小波分解与改进GWO-SVM的道岔故障诊断

孔令刚，焦相萌，陈光武，范多旺

基于Mallat小波分解与改进GWO-SVM的道岔故障诊断

孔令刚3，焦相萌1, 2，陈光武1, 2，范多旺1, 2

(1. 兰州交通大学 自动控制研究所，甘肃 兰州 730070；2. 甘肃省高原交通信息工程及控制重点实验室，甘肃 兰州 7300703；3. 兰州交通大学 国家绿色镀膜技术与装备工程技术研究中心，甘肃 兰州 730070)

为顺应道岔故障诊断向智能化和自动化的发展趋势，以S700K转辙机功率曲线为例，提出一种改进型灰狼优化算法(GWO)与支持向量机(SVM)相结合的故障诊断方法。在8种故障模式和正常模式所对应的功率曲线实施5层Mallat小波分解，得到各层近似系数和细节系数，并计算各层系数的平方和；利用主成分分析法对系数平方和组成的向量集进行降维，得到特征向量集；改进型灰狼优化算法优化支持向量机参数，并用优化好的支持向量机进行故障预测。研究结果表明：该方法能有效提高道岔故障诊断的准确率。

道岔故障诊断；支持向量机；S700K转辙机；灰狼优化算法；Mallat小波分解

道岔是一种直接关系到铁路系统安全运营的关键信号设备，目前对其状态分析主要靠微机监测系统与人工结合的方式。这种方式与铁路向着智能化、自动化和信息化的发展趋势相悖。近年来，不少专家和学者从事这方面的研究。赵林海等[1]提出基于灰关联的诊断方法，该方法的优点是无需训练，实现起来简单，不足之处是主观性强。Atamuradov等[2]提出用专家系统的诊断方法，不足之处是专家经验获取困难；董炜等[3]提出群决策诊断方法，该方法融合众专家意见，使得信息更加完整，不足之处是算法较为费时且存在“从众现象”。董海鹰等[4]提出基于D-S证据理论诊断方法，该方法易于描述不确定性问题，不足之处是缺乏自学习能力。雷汝海等[5]提出Mallat小波分解的电网谐波检测方法，实现基波与谐波成分分离。王志华等[6]提出混沌灰狼优化算法的SVM分类器，并验证该分类器分类准确率高和误差小。陈闯等[7]提出IGWO-SVM的分类器，实现对语音情感高准确识别。本文提出一种基于Mallat小波分解与改进GWO-SVM相结合的道岔故障诊断方法。该方法更加有效提取功率曲线特征，避免支持向量机2个参数选取的主观性，降低训练过程中陷入局部最优的概率和提高故障类型分类的准确率。本文主要工作：首先，对功率曲线数据实施小波分解，得到各层近似系数(Approximation Coefficient, cA)和细节系数(Detail Coefficient, cD)，并计算各层系数的平方和；其次，对系数平方和组成的向量集进行降维，得特征向量集；最后，利用改进的灰狼优化算法优化支持向量机参数，并用优化好的支持向量机进行故障预测。仿真结果表明，优化后的分类器具有更高的分类准确率。

1 S700K转辙机工作状态

S700K型交流转辙机是高速铁路上常用的转辙机，并且和ZYJ7等转辙机功率输出规律相似，具有一定的代表性。所以针对S700K的研究方法也可以迁移应用到其他类型上。本文以S700K为例展开研究。

1.1 S700K正常工作状态

S700K型转辙机正常输出功率曲线如图1所示。该曲线分为5个阶段：启动、解锁、转换、锁闭和构通表示。启动时，大约在0.2 s处，输出一个较大功率；在解锁、转换与锁闭阶段，输出功率相对稳定，在0.5 kW左右；构通表示结束后，输出功率为0。

图1 S700K正常运行的功率曲线

表1 S700K常见故障现象及原因

1.2 S700K故障工作状态

查阅相关文献，目前高速铁路上的道岔，主要出现8种故障类型[1]。S700K常见故障现象及原因如表1所示。8种故障类型所对应的S700K转辙机功率曲线如图2所示，故障号依次标记为{F1，F2，F3，F4，F5，F6，F7，F8}，为方便统一描述，正常状态故障号标记为{F0}。分别在9种模式的功率曲线上每间隔0.02 s抽取一个采样点，抽取7 s长，各获得350个采样点，作为原始样本。

(a) 故障类型1；(b) 故障类型2；(c) 故障类型3；(d) 故障类型4；(e) 故障类型5；(f) 故障类型6；(g) 故障类型7；(h) 故障类型8

2 特征提取

2.1 Mallat算法小波分解

Mallat算法是一种快速实现离散小波变换的算法。它能把所需要分析的信号二分解到各个频率尺度，其等效为对信号实施多次低通和高通滤波，从而得到不同层近似系数(低频系数)和细节系数(高频系数)；小波分解树如图3所示(5层小波分解为例)。小波分解过程如图4所示。分解式如式(1)所示。具体相关理论推导过程参见文献[8−9]。

图3 小波分解树

图4 Mallat算法分解过程

使用db3小波基对各功率曲线做5层小波分解，得到各层系数{cA1，cA2，cA3，cA4，cA5，cD1，cD2，cD3，cD4，cD5}。以正常功率曲线的小波分解为例，各层系数如图5所示。

图5 正常功率曲线各层系数

计算各小波系数平方和：分别计算各层近似系数和细节系数各自的平方和(如表2和表3所示)，分别记作{ScA1，ScA2，ScA3，ScA4，ScA5，ScD1，ScD2，ScD3，ScD4，ScD5}。为方便叙述，定义ScA为近似系数方和(Sum of Squared Approximation Co-efficients)；定义ScD为细节系数方和(Sum of Squares of Detail Coefficients)；系数方和包括近似系数方和与细节系数方和。

表2 近似系数方和

表3 细节系数方和

2.2 主成分分析法

主成分分析法能够实现对输入向量进行降 维[10]。该算法去掉冗余的变量，保留互不相关的变量；该算法使得保留最少变量的同时，尽可能最大的保留原始信息。其降维步骤如下：

1) 设矩阵×由[ScA1，ScA2，ScA3，ScA4，ScA5，ScD1，ScD2，ScD3，ScD4，ScD5]T组成(包含10个指标)，为和系数的个数(变量个数)，为10；为功率曲线的个数(样本个数)，=9。对×每一行元素a，实施归一化处理(=1，2，…，10)，得到×(每一行元素b)；对×进行协方差计算，得到协方差矩阵×，计算公式如式(2)和式(3)。

式中：×为归一化矩阵，目的是消除各指标量纲和数量级的差别。

2) 计算协方差矩阵特征值，并由大到小排列得和所对应的特征向量，(=1，2，…，)。

3) 按照式(4)计算各变量的贡献率C，按照式(5)计算累计贡献率SC，(＜)；并找到一个最小的正整数，使得累计贡献率达到80%以上，此时特征值{1，…，λ}分别对应{第1主成分1，…，第主成分M}，从而将输入空间由维映射到维。本节计算出的特征值及各主成分贡献率如表4所示。

表4 特征值及各主成分贡献率

式中：C表示第个主成分M的贡献率，值越大，在各主成分中的影响力越大。

式中：SC表示前个主成分的累计贡献率。

一般以SC达80%~90%，选取主成分个数。

4) 主成分载荷分析：按照式(6)计算各主成分与各个变量之间的主成分载荷；得到的结果：第1主成分1和{ScA1，ScA2，ScA3，ScA4，ScA5，ScD1，ScD2，ScD5}有较大的正相关，且ScA1和1有最大正相关，故ScA1可作为该类代表；第2主成分2和{ScD3，ScD4}有较大的正相关，且ScD3和2有最大正相关，故ScD3可作为该类代表。故输入特征向量为[ScA1 ScD3]T。

式中：M表示第主成分；a表示第个原变量；表示第个主成分所对应的特征值；表示第个主成分所对应的特征向量第个元素。

3 灰狼优化算法和支持向量机

3.1 灰狼优化算法

灰狼优化算法(Grey Wolf Optimization Algorithm, GWO)是一种模拟灰狼捕食猎物活动的元启发式算法[11]。GWO具有易实现、收敛性强和参数少等优点。GWO算法流程图如图6所示。灰狼是等级森严的群体，GWO算法模拟等级将狼群分为(，，，)4个等级；GWO算法模拟狼群狩猎的3个过程：包围猎物(Encircling Prey)、猎捕猎物(Hunting Prey)和攻击猎物(Attacking Prey)。

3.1.1 包围猎物

狼群寻找猎物时，逐渐靠近猎物并包围猎物，该过程数学表达式为式(7)。

式中：“°”表示Hadamard乘积；t表示当前迭代次数；Xp(t)为猎物的位置向量；X(t)为当前灰狼的位置向量；A和C都为协同系数向量；a是收敛系数向量，并且a的每个分量aj在迭代过程中，由2线性降至0，(j=1，2，…，n)；T为最大迭代次数；r1和r2是随机向量，各维分量在[0 1]上取值。

3.1.2 猎捕猎物

包围猎物(潜在最优解)之后，狼群依靠搜寻猎物的能力进行围捕(狼群进行位置更新)；位置更新的示意图如图7所示。算法在迭代过程中，保留性能最好的3只灰狼(，，)，头狼的位置代表全局最优解；狼代表全局第2优解；狼代表全局第3优解，狼群根据(，，)调整位置。位置更新数学表达式为式(8)，式(9)和式(10)。

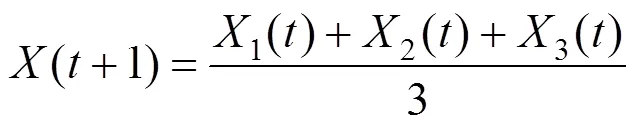
式中：()，()和()分别表示狼(，)当前位置向量；()代表当前灰狼的位置向量；()，()和()分别表示当前灰狼到狼(，，)的距离向量。

图7 灰狼位置更新示意图

3.1.3 攻击猎物

攻击猎物是狼群狩猎的最后一步，该过程是捕捉猎物的过程，也是得到最优解的过程。该过程通过线性递减向量实现协同系数向量取值范围缩小。如图8所示：当║║≤1时，狼群向猎物聚集，实现对猎物抓捕，从而得到最优解；当║║＞1时，狼群四散，远离猎物，算法发散。

图8 搜寻猎物和攻击猎物示意图

3.2 GWO算法改进

GWO算法虽有较强收敛性能，但有可能收敛于局部最优[12]。这是因为狼位置坐标不一定对应全局最优坐标点，可能在各次迭代中，狼逐渐靠近(，，)这3只狼，从而导致算法陷入局部最优。为增加全局搜索能力和有效保证局部搜索能力，本文提出非线性动态变化式的收敛系数向量，如式(11)所示(以2为半径，以(0,0)为圆心，以/为自变量的1/4圆)。

3.3 支持向量机

支持向量机是一种分类算法，可以解决线性可分问题、近似线性可分问题和线性不可分问题。对于解决这3类分类问题，分别训练线性可分支持向量机、线性支持向量机和非线性支持向量机。解决线性不可分问题的本质是将样本非线性映射到高维特征空间，然后在高维特征空间设计一个线性支持向量机，间接实现对样本的分类，即将线性不可分问题转化为线性可分问题或者近似线性可分问题。支持向量机的相关理论推导参见文献[13]。实现非线性映射的核函数有线性核、多项式核、高斯核、拉普拉斯核和核等，由于高斯核具有普适性且应用最广，本文选高斯核，如式(12)；目标函数为式(13)，约束条件为式(14)，支持向量机需要学习的参数为和，由GWO算法进行优化。

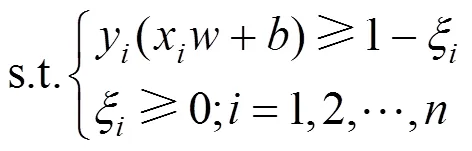
式中：参数为惩罚因子，表示对误差的宽容度。过大，易出现过拟合；过小，易出现欠拟合；参数体现支持向量的个数，而支持向量的个数直接影响训练和预测的速度。过大，支持向量个数越少；过小，支持向量个数越多；为松弛变量；为样本个数。

3.4 算法流程

1) 样本归一化。将由[ScA1 ScD3]组成的样本分为训练样本和测试样本，并将样本进行归一化处理，即将样本映射到[0,1]区间上。

3) 初始化参数。需要初始化的参数有：①狼群规模；②最大迭代数；③惩罚因子的取值范围和初始取值；④高斯核函数参数的取值范围和初始取值(和组成狼位置坐标向量)。

4) 随机初始化各灰狼的位置坐标。

5) SVM依据初始和初始进行初次训练，并计算每只狼的初始适应度。

6) 按照适应度值，将狼群分为(，，，)４个等级。

7) 依据式(7)～(9)更新各灰狼位置坐标。

8) 计算各灰狼新位置处的适应值new，并与上次迭代过程中的全局最优适应值F做比较；如果new＞F，则F替换掉new；反之，不用进行替换。

9) 如果迭代次数已经达到或者全局适应度值小于预设最大适应度(常数)，终止算法，输出全局最优位置(_，_)；反之，返回步骤(6)，继续执行优化。

10) SVM使用最优参数(_，_)对测试样本进行预测。

3.5 故障诊断系统结构框图

样本分为训练样本和测试样本。故障诊断系统分为特征提取、模型优化和故障预测3个部分。故障诊断系统结构框图如图9所示。

图9 故障诊断系统结构框图

4 仿真与分析

4.1 仿真准备工作

4.1.1 样本扩充

用Excel中RAND()函数扩充样本，即在不同故障类型功率曲线加入不同程度波动。新增81组扩充训练样本(每类增加9组)和36组扩充测试样本(每种故障类型增加4组)；将第1～81组作为训练集，第82～126组作为测试集。

4.1.2 初始化改进的GWO-SVM模型

GWO算法参数初始化：狼群规模=15；最大迭代次数为200；预设最大适应度为0.01。

4.2 仿真过程的分析

4.2.1 仿真与准确率比较

本节将改进GWO-SVM模型、未改进GWO- SVM模型以及SVM模型做准确率比较。改进GWO-SVM模型经过18次迭代，诊断误差(适应度值)达到0，终止迭代，其预测结果如10(a)所示，其误差图如10(b)所示，准确率为100%；GWO-SVM模型经200次迭代后，终止循环，误差未小于0.01，陷入局部最优，其预测结果如10(c)所示，其误差图如10(d)所示，准确率为97.2%(35/36)；SVM模型(取65.07，取0.86)的预测结果如10(e)所示，其误差图如10(f)所示，预测准确率为91.7%(33/36)；此外，本节将改进后的GWO-SVM模型与CS-SVM模型、PSO-SVM模型做预测错误率比较(如表5所示)；由表5数据可知：改进后的GWO-SVM模型预测错误率最低，为0%，说明该模型具有较高诊断准确率且优于表中其他方法。

(a) 改进GWO-SVM；(b) 误差；(c) 未改进GWO-SVM；(d) 误差；(e) SVM；(f) 误差

4.2.2 附加条件判断

由图10()和图10()可知，误诊的故障类型为类型4与类型7；通过观察这2种功率曲线：故障类型4的功率曲线大约在第310个采样点以后，功率为0；而故障类型7在第310个采样点以后，功率不为0且大于0.2 kW；故可判断第335个采样点是否大于0.15 kW作为区分类型4和类型7的依据，从而增加诊断的准确率。

表5 预测错误率

5 结论

1) 以S700K转辙机功率曲线为例，提出改进Mallat-GWO-SVM道岔故障模式分类模型。该方法以Mallat小波变换和主成分分析法为基础，提取特征向量；以改进GWO-SVM为分类器，进行故障类型分类。

2) 仿真结果表明：该方法能提高故障诊断准确率，从而验证该方法的有效性。

[1] 赵林海, 陆桥. 基于灰关联的道岔故障诊断方法[J].铁道学报, 2014, 36(2): 69−74. ZHAO Linhai, LU Qiao. A method for fault diagnosis of turnout based on grey correlation[J]. Journal of the China Railway Society, 2014, 36(2): 69−74.

[2] Atamuradov V, Cammci F, Baskan S, et al. Failure diagnostics for railway point machines using expert systems[C]// IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives. New York: IEEE Press, 2009: 1−5.

[3] 董炜, 刘明明, 王良顺, 等. 基于群决策的道岔控制电路故障诊断方法[J]. 自动化学报, 2018, 44(6): 1005− 1014. DONG Wei, LIU Mingming, WANG Liangshun, et al. Fault diagnosis for railway turnout control circuit based on group decision making[J]. Acta Automatica Sinica, 2018, 44(6):1005−1014.

[4] 董海鹰, 李娜. 基于D-S证据理论信息融合的转辙机故障诊断方法研究[J]. 测试技术学报, 2013, 27(1): 1−7. DONG Haiying, LI Na. Fault diagnosis method for switch machine based on D-S evidence theory information fusion[J]. Journal of Test and Measurement Technology, 2013, 27(1): 1−7.

[5] 雷汝海, 郝震. 基于小波变换Mallat算法的电网谐波检测方法[J]. 工矿自动化, 2014, 40(12): 65−69. LEI Ruhai, HAO Zhen. A harmonic detecting method for power grid based on wavelet transform mallat algorithm[J]. Industrial Mining Automation, 2014, 40(12): 65−69.

[6] 王志华, 罗齐, 刘绍廷. 基于混沌灰狼优化算法的SVM分类器研究[J]. 计算机工程与科学, 2018, 40(11): 2040−2046. WANG Zhihua, LUO Qi, LIU Shaoting. An SVM classifier based on chaotic gray wolf optimization algorithm[J]. Computer Engineering and Science, 2018, 40(11): 2040−2046.

[7] 陈闯, Ryad Chellali, 邢尹. 改进GWO优化SVM的语音情感识别研究[J]. 计算机工程与应用, 2018, 54(16): 113−118.Chen Chuang, Ryad Chellali, Xing Yin. Research on speech emotion recognition based on improved GWO optimized SVM[J]. Computer Engineering and Applications, 2018, 54(16): 113−118.

[8] Mallat S. A theory for multiresolution signal decomposition: The wavelet representation[J]. IEEE Transaction on Pattern Analysis andMachine Intelligence, 1989, 11(4): 674−693.

[9] 白润才, 柴森霖, 刘光伟, 等. 基于Mallat算法与ARMA模型的露天矿卡车故障率预测[J]. 中国安全科学学报, 2018, 28(10): 31−37. BAI Runcai, CHAI Senlin, LIU Guangwei, et al. Method for predicting truck’s failure rate in open-pit mine based on Mallat algorithm and ARMA model[J]. China Safety Science Journal, 2018, 28(10): 31−37.

[10] Hervé A, Williams L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews Computational Statistics, 2010, 2(4): 433−459.

[11] Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014(69): 46−61.

[12] Heidari A A, Pahlavani P. An efficient modified grey wolf optimizer with lévy flight for optimization tasks[J]. Applied Soft Computing, 2017(60): 115−134.

[13] 雷烨. 基于粒子群最小二乘支持向量机的故障诊断算法研究[D]. 兰州: 兰州交通大学, 2010: 18−24. LEI Ye. Research on fault diagnosis algorithm based on particle swarm least squares support vector machine[D]. Lanzhou: Lanzhou Jiaotong University, 2010: 18−24.

Turnout fault diagnosis based on Mallat wavelet decomposition and improved GWO-SVM

KONG Linggang3, JIAO Xiangmeng1, 2, CHEN Guangwu1, 2, FANDuowang1, 2

(1. Automatic Control Institute, Lanzhou Jiaotong University, Lanzhou 730070, China;2. Gansu Provincial Key Laboratory of Traffic Information Engineering and Control, Lanzhou 730070, China;3. National Engineering Research Center for Technology and Equipment of Environmental Deposition, Lanzhou Jiaotong University, Lanzhou 730070, China)

In order to adapt to the development trend of intelligent fault diagnosis, this paper took the power curve of S700K switch as an example, and proposed a fault diagnosis method based on improved Gray Wolf Optimization Algorithm (GWO) and Support Vector Machine (SVM). Firstly, five layers of Mallat wavelet decomposition were performed on the power curves corresponding to the eight failure modes and the normal mode, and the approximate coefficients and detail coefficients of each layer were obtained. The square sum of the coefficients of each layer was calculated. Secondly, the principal component analysis method was used to reduce the dimension of the vector set composed of the squares of the coefficients to obtain the feature vector set. Finally, the improved gray wolf optimization algorithm optimized the support vector machine parameters, and the optimized support vector machine was used to predict the fault. The simulation results show that the method can effectively improve the accuracy of turnout fault diagnosis.

turnout fault diagnosis; support vector machine; S700K switch machine; grey wolf optimization algorithm; Mallat wavelet decomposition.

U284.92

A

1672 − 7029(2020)05 − 1070 − 10

10.19713/j.cnki.43−1423/u.T20190760

2019−08−30

国家科技支撑计划资助项目(2014BAF01B00)；甘肃省科技计划资助项目(18JR3RA116)；甘肃省高等学校科研资助项目(2018C-11，2018A-22)；甘肃省自然科学基金资助项目(18JR3RA130，18JR3RA110)

孔令刚(1978−)，男，安徽合肥人，副教授，从事铁路信号设备故障诊断研究；E−mail：konglinggang1978@163.com

(编辑 蒋学东)