考虑经济效益的风储联合发电系统的最优功率预测

任立阳，付 昱，王宝财，宋田宇，赵芳琦

(1.东北电力大学电气工程学院，吉林 吉林 132012；2.中国电力科学研究院，北京100000)

近年来，随着生态环境的污染加剧和化石能源的越发枯竭，清洁能源受到世界各国的重视，而其中风能作为一种极其重要的清洁能源，得到快速发展[1].然而，风资源本身具有随机性和强波动性，这导致风电场的输出功率具有较强的不稳定性[2].这一特性对电力系统的稳定运行和正常调度产生了较大的负面影响[3]，同时也会降低风电场和电力系统的经济性.因此建立一种提高经济效益的风功率预测和电力系统调度模型尤为重要.

较为精准的风功率预测不仅是制定合理的调度计划和检修计划的基础，而且是提高风能利用率和电网运行的安全性、经济性和稳定性的有力措施.国内外学者对风功率预测问题已有较多研究，取得了一些成果.文献[4]中基于经验小波变换和核极限学习机建立了短期风功率预测模型.文献[5]中采用时间序列法对原始风功率序列进行处理从而进行预测，该文献的结果说明不考虑气象因素的预测模型的结果不够理想.文献[6]中基于训练好的BP神经网络进行风功率预测，同时对模型的权值和阀值使用遗传算法进行优化.文献[7]中提出了一种基于卡尔曼滤波的风功率预测模型，该模型将风电输出功率预测与数值天气预报数据结合以提高模型的预测精度.上述文献中所提出的预测方法虽然在一定程度上都对传统风功率预测模型进行了一定改进，但是需要以庞大的数据库作为支撑，同时这些方法并未以风电场的经济效益为预测目的来构建风功率预测模型.

电力系统的调度的经济性也是研究者的关注点之一.文献[8]针对不同的风电渗透率分析了弃风的原因，并以风电并网的电量最大化和风电经济性最高为目标函数建立模型.文献[9]提出了一种基于弃风最小的综合优化配置方法，同时给出不同场景下的风电和储能的最优经济调度策略.文献[10]提出了一种调用储能资源的电力系统优化调度模型，并运用两阶段动态规划法求解.文献[11]提出了一种利用大容量储能电池来提升风电调峰能力的充放电调度策略，通过储能为降低弃风，提高系统经济性提供较为效的解决措施.文献[12]中提出一种综合考虑储能电站的造价成本和风电接纳的效益成本的储能模型，对储能资源容量进行优化配置.这些模型通过降低弃风或采用风电储能运行方式等来提高电力系统的稳定性和经济性，并未在风功率预测之初就考虑风电效益性.

为了降低风功率预测误差成本以及提高电力系统的经济性，本文构建了基于成本导向函数的风功率预测模型及实时电价控制策略下的储能调度模型.首先采用基于成本导向的增强回归树模型进行风功率预测，在成本导向损失函数下，预测结果达到平均成本最小.其次，利用预测的风功率，以日前调度计划阶段确定的储能运行状态为基础，在日内调度计划中使用基于成本导向的增强回归树模型所得的风功率预测数据进行调度建模.最后在两个风电场中验证本文所提方法的有效性和先进性.

1 改进的增强回归树

1.1 回归树基本原理

回归树是文献[13]中提出的一种非参数学习技术.与一般线性模型和支持向量机等参数学习算法不同，回归树在学习过程中未明确采用指定的参数功能形式.回归树使用自顶向下和分治法将观测值递归地划分为越来越小的非重叠区域.划分过程是二进制的，每个区域中的观测值被分配为具有均质响应.然后，将其与输出在同一区域中的所有观测值拟合为均值响应.回归树表示为

(1)

公式中：M为区域的数量；cm为每个区域中观测值的平均响应；Rm为每个区域的分区；I(x∈Rm)为一个指标函数，如果x∈Rm则等于1，否则为0.

给定由N个观测值(xi，yi)组成的训练数据，其中i=1，…，N，每个观察都有p输入和响应.

因此回归树的构建步骤如下：

(1)从包含所有观察结果的单个区域开始.然后搜索所有变量的二进制分割，找到第j个分裂变量x(j)和分裂点s，这将尽可能地减少误差.为了找到最佳的分裂变量和分裂点，采用下述公式

,

(2)

使搜索过程得以解决.

(2)在每个新区域中，重复(1)来拆分并创建两个新区域.

(3)重复分割过程，直到达到停止标准为止，例如，当达到每个区域的最小观察次数时停止分割过程.

其原理流程图，如图1所示.

1.2 Boosting基本原理

Boosting是一种提高模型准确性的方法，最初是针对分类问题[14]开发的，后来扩展到回归问题[15].Boosting源自计算学习理论，即弱学习和强学习问题相等[16].它通过适合许多基础学习者(弱学习)并将它们组合在一起以获得更准确的模型(强学习)来提高模型性能.在提升过程中，基础学习者在每次迭代时都被顺序地应用于训练数据，并且对训练数据进行了修改以增加对现有基础学习者建模效果较差的观察结果的重视.依次将基础学习者添加到模型中，而无需一次调整一个参数，直到所有参数都进入模型为止[12].提升模型的公式为

(3)

公式中：M为基础学习者的数量；h(x；am)为基础学习者；am为基础学习者的参数.

1.3 以成本为导向的增强回归树

使用回归树作为基础学习者并提高成本导向的损失函数，能够将与可再生能源发电的预测误差相关的实际成本纳入模型构建和预测过程.一般成本导向损失函数为

(4)

(1)Lco(0)=0.表示若预测误差为零，则没有成本；

(5)

因此，将公式(4)代入公式(5)，最优预测为

(6)

给定成本导向的损失函数公式(4)，最优预测便是公式(6).通过在函数空间中应用优化来求解公式(6).增强过程中将最适合公式(4)的负梯度向量的回归树添加到每个步骤的扩展中.该方法的步骤如下：

(1)初始化F0(x)=0.

(2)对于m=1，…，M，执行以下操作：

(a)计算当前模型的负梯度

(7)

(c)更新当前模型：

Fm(x)=Fm-1(x)+ρmT(x；Θm)

，

(8)

公式中：ρm为步长.

(3)在顺序添加所有M个回归树时构建模型.

(4)使用生成的模型对风电场中的风功率进行预测.

为防止过度拟合，在(2)的(c)中使用收缩参数λ[18]，λ的典型值为0.01或0.001.

Fm(x)=Fm-1(x)+λρmT(x；Θm)

.

(9)

2 计及实时电价的储能模型

2.1 实时电价

所谓实时电价即在一天之内各时段所对应的不同用电状态所产生的具有实效性的费用价格，该价格在满足电力市场的供需关系基础上，通常还受整体电力市场下生产方、销售方及用户等相互之间的竞争、制约及收益关系影响，通常实时电价的曲线随时间的实时变化呈现波动趋势，本文引入某时段的美国加州电价进行分析[19]，同时结合我国实际市场状况建立实时电价模型，如图2所示.

2.2 基于电价运行控制策略的储能模型

随着电力市场大环境中各方面的性能优化不断改进，对于用户而言，实时电价的提供也将变得越来越清晰智能，但电价信号作为能够实时反映电力需求的可靠参考指标，若能够有力地掌控当前电价制度下储能用户的充放电规律，则对于通过电价调节手段实现储能资源的有效调度起到重要作用.本文基于以上分析，将储能系统的充放电规律与不同储能用户的行为习惯相结合，并在此基础上构造出与其相应的电价因子，同时以此为依据模拟出电价控制策略下的储能充放电负荷曲线，构造电价影响因子为

ΔGPi=GPavg-GPi

，

(10)

(11)

(12)

公式中：GPj为电力市场一天内的实时电价；GPavg为日平均电价；ΔGPj为日均电价与实时电价间的差价；j(j=1，2，…，96)是每日96个均匀时刻点.

Pj=λjP

.

(13)

2.3 风储联合系统的调度建模

2.3.1 目标函数

风储联合系统采用削峰填谷和计划跟踪多模式协调运行方式[20].基于风电的不确定性，本文将风储联合系统的整体收益期望最大化为优化方向.目标函数为

(14)

2.3.2 约束条件

风储联合系统协调优化模型的约束条件包括对电量、充放电功率以及储能循环费用的限制，具体表示以下：

(1)电量约束

(15)

(2)充放电功率限制约束

(16)

(3)储能循环费用的可行域约束

(17)

3 考虑经济效益的风功率预测及风储联合系统调度建模

3.1 评估指标

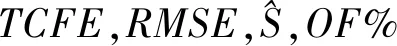
(1)与预测错误相关的总成本(TCFE).TCFE通过使用预测来衡量成本，是文献[21，22]中提出的评估指标的扩展.

(18)

公式中：ei为第i个测试样本的预测误差；n为总测试样本的数量.

(2)均方根误差(RMSE).RMSE对预测结果的极值比较敏感.

(19)

(20)

(4)过度预测百分比(OF%)和预测不足百分比(UF%)比.OF%和UF%测量零附近的不对称量.OF%表示测试集中过度预测样本的百分比，UF%表示测试集中预测不足的百分比.

(21)

公式中：nof为过度预测样本的数量；nuf为预测不足样本的数量.

3.2 考虑经济效益的风储联合系统的优化调度

为降低弃风电量，提高风储联合系统的经济效益，从而提高电力系统的经济性，本文提出考虑经济效益的风功率预测模型和风储联合系统优化调度模型.

3.2.1 考虑经济效益的风功率概率预测模型

本节介绍考虑成本导向的增强回归树建立的风功率预测模型.该模型以成本为导向优化增强回归树的损失函数，提高风功率预测精度的同时降低风功率预测误差成本，从而提高经济效益.基于成本导向的增强回归树的风功率预测模型(COBRT)流程图，如图3所示.为了进行比较，选择常规增强回归树(BRT)和最小二乘增强回归树(LSBRT)作为对比实验，验证本文所提模型COBRT的先进性.

3.2.2 风储联合系统优化调度建模

本节基于模型COBRT得到的风功率预测值，建立风储联合系统优化调度模型.公式(14)至公式(17)构成本文的协调优化模型，通过求解该模型可得到风储联合系统的日前发电计划和各不确定性场景中储能的充放电功率.采用PSO与GAMS软件中CPLEX求解器相结合的混合策略对本文提出的双层优化配置模型进行求解.具体步骤如下：

(1)使用模型COBRT进行风功率预测值，输出96个风功率预测值；

(2)将目标函数设置为风储联合系统整体收益最大；

(3)风储联合系统协调优化模型的约束条件考虑电量约束，充放电功率限制约束和储能循环费用的可行域约束，具体根据2.3.2；

(4)建立风储联合系统协调优化模型并使用CPLEX求解；

(5)输出常规发电机组和风电机组的出力情况；

(6)根据风电机组计划出力和实际出力的差值求得风电机组的剩余出力；

(7)结合实时电价曲线和储能电池的基本要求，得到风电场实际储能充放电功率曲线和存储量；

(9)确定风储联合系统的调度结果和最终的风能存储量结果，计算经济收益；

(10)对比分析本文所提模型的经济性.

4 算例分析

4.1 实验数据

表1 数据集划分

以我国两个风电场为预测对象，验证模型COBPR的性能.A风场的总装机容量为300 MW，并网机组台数200台.B风场的总装机容量为400.5 MW，并网风机台数为267台.取A风场2018年1月1日到12月31日的风电功率数据(采样间隔是15 min)，B风场2018年1月1日到12月23日的风电功率数据(采样间隔是15 min)分别构建与验证预测模型.数据集的划分,如表1所示.

为消除数据量纲对模型性能的不良影响，防止数值小的表征被数量级大的表征数据淹没，需要对数据率先进行归一化处理.计算公式为

(22)

数据预处理完成后，使用训练集确定增强回归树模型的网络参数，建立基于成本导向的增强回归树预测模型.

4.2 风功率预测结果分析

如3.2选择模型BRT和模型LSBRT作为对比实验，将这两种模型和模型COBRT的风功率预测结果对比分析，验证本文所提模型COBRT的性能.

图4 风电场A的预测结果图5 风电场B的预测结果

风电场A和风电场B中，采用模型COBRT、模型LSBRT、模型BRT进行的为期一天的风功率预测，如图4、图5所示.分析图4、图5发现：模型LSBRT的预测结果与原始风功率的变化趋势较为相近，模型COBRT次之；当原始风功率序列变化较大时，模型LSBRT也可以得到最符合原始风功率序列的预测结果.表明本文所提模型LSBRT的预测值更接近原始真实的风功率.这是因为LSBRT损失函数的目的就是为了达到预测误差的最小化，而模型COBRT的损失函数是基于成本导向的，是为了达到经济效益最大化.这也反映出该方法在预测过程中产生的误差越小，那么该方法的所达到的经济收益就越高.

表2 风电场A的5种评估指标

表3 风电场B的5种评估指标

为更全面详细的说明模型COBRT的性能，列举了风电场A和风电场B的3种模型的5个指标结果如表2、表3所示.分析表2、表3可以发现：

(1)模型LSBRT的RMSE，MAE和MAPE值总是比使用COBRT方法的小，也就是说，LSBRT可以得到更准确的预测值.这是因为建立了LSBRT是为了最小化RMSE，MAE和MAPE.

(2)风电场A中，模型COBRT的TCFE值比模型BRT和模型LSBRT的TCFE值分别小105.7和41.1.风电场B中，模型COBRT的TCFE值比模型BRT和模型LSBRT的TCFE值分别小123.5和40.8.

由于本文的研究目的是为了让经济效益最大化，因此与模型LSBRT和模型BRT相比，使用模型COBRT减少了风电场的总负荷，可以使风电场获得最大的经济性收益.

4.3 储能的实验结果分析

基于本文构建的风储联合系统的调度结果如图6、图7所示.风电场计划出力与实际出力的差值，便是该风电场可以用来存储的功率值.但是这些风电是卖出还是进行储能，需要根据实时电价确定.分析图6、图7可知：0点～9点和14小时～16小时这两个阶段是负荷低谷期，剩余风电量比较多，而此时的电价较低，因此这两个时段将弃风进行存储，储能电站处于充能状态.10点～13点和15点～24点这两个时段是负荷高峰期，此时电价有明显涨幅.为了达到经济效益最大化，储能电站处于放电状态，将上段时刻存储的风电卖出.通过该协调策略可使系统的经济性最佳.

图6 A风电场储能真实功率变化及存储量图7 B风电场储能真实功率变化及存储量

表4 风储联合系统的经济收益情况

表5 储能模型收益对比情况

为更直观说明本文所建模型的有效性，表4分别列出了风储联合系统A和B的各经济指标.表5列出了普通风电场、传统储能电站及所提模型的经济效益对比.可以看出本文所提模型相对比于传统的储能系统可使风储联合系统获得更大的经济效益，风电机组的计划出力与实际出力的差值势必存在较大差值.实时电价控制策略下的风储联合系统在最大程度利用风电的基础上，将剩余的风电在电价较低时存储起来，电价较高时售出，可以大大提高风电的利用率，并且还能兼顾电力系统经济效益.

5 结 论

考虑经济效益的风功率预测和风储联合系统优化调度不仅可以更大程度的利用风电，提高风电场运行中经济效益，而且可以更好的为电力系统决策人员提供有利参考.本文采用的考虑经济效益的风电功率预测和风储联合系统的优化调度方法有以下优点：

(1)使用增强回归树进行风功率预测，并基于成本导向函数优化增强回归树，在得到较高精度的风功率预测结果的同时，降低风功率在预测过程中产生的误差成本，提高风电场的经济效益；

(2)基于高精度和高经济性的风功率概率预测，建立电力系统经济调度模型，该模型可以得到更好的调度结果；

(3)结合实时电价曲线，储能电站在负荷低谷期存储剩余的风电，在负荷高峰期卖出，达到经济效益最大化.