基于支路模式势能的含高比例DFIG电网低频振荡特性分析

刘 铖，杨 慧，王 旭，于思瑶，赵晓洋

(现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学)，吉林 吉林 132012)

针对全球环境恶化和化石资源枯竭等问题，为促进资源友好型、资源节约型社会建设，风能作为清洁和可再生能源发展十分迅速[1-2].其中，能够快速解耦有功功率和无功功率，并为电网提供无功和电压支持的双馈风机(Double-Fed Induction Generator，DFIG)，在电网中得到广泛使用.但是，随着风电并网的规模不断扩大，电源侧结构发生改变，电网呈现低惯量态势越加明显[3-5]，加上风机的出力具有波动性和不确定性，对电网功率平衡也带来了一定的影响，因此，研究含高比例DFIG并网电力系统小干扰稳定性具有一定的实际意义.

目前，对于DFIG并网后小干扰稳定问题，国内外诸多学者针对该问题做了大量研究[6-14].文献[6-8]通过详细的DFIG模型分析了DFIG接入电网对系统阻尼的影响.文献[9～10]利用特征值分析法分析了DFIG接入对电网小干扰稳定性的影响.由于振荡中心的电压最低，振荡幅度最大，因此，为了能够了解风电接在振荡中心对系统的影响，文献[11]将风电接在近振荡中心位置，分析了风电场并网对电网阻尼的影响.文献[12～13]通过对系统仿真，分析了DFIG接入对系统阻尼的影响.文献[14]分析了DFIG接入后风速变化对系统振荡模式的影响，文献[15～17]通过转矩分析法分析了风电运行状态对系统振荡模式的影响.由上述可知，目前小干扰稳定分析方法主要有转矩分析法和特征值分析法，但是，目前研究大多都是从发电机角度研究DFIG并网后对系统阻尼和振荡模式的影响.

电力系统发生低频振荡时，其显现和传播主要体现在电网传输线路中，从该角度分析低频振荡的分布特性可揭示更多振荡信息.为了进一步研究高渗透率DFIG并网电力系统振荡模式的分布特性，借鉴能量函数思想[18]，本文利用支路模式势能法[19]，以WSCC3机9节点电力系统为例，研究不同风电渗透比下风电接入电网和替换电网中同步发电机两种情况下对系统不同模式下振荡割集的影响.

1 DFIG数学模型

DFIG定子与转子绕组的d-q轴电压为

(1)

公式中：uds和uqs分别为d轴和q轴定子电压；udr和uqr分别为d轴和q轴转子电压；ids和iqs分别为d轴和q轴定子电流；idr和iqr分别为d轴和q轴转子电流；rs为定子电阻；rr为转子电阻；xs为定子电抗；xm为电磁电抗；xr为转子电抗；ωm为转子角速度.

DFIG注入电网的功率表达式为[20-21]

(2)

(3)

公式中：Pi和Qi分别为风机注入电网的有功和无功功率，ui为节点电压.

2 含DFIG电力系统的模式势能构建

含DFIG电力系统的动态特性可由一组非线性微分方程和一组代数方程表示为

(4)

电力系统进行小干扰分析时，对系统动态响应的高阶次非线性方程进行线性化处理.因此，电力系统非线性微分代数方程在平衡点线性化后的矩阵表达形式为

(5)

公式中：ΔX=[Δxδi，Δxωi，ΔxDFIG，Δxzi]T，其中，Δxδi，Δxωi，为同步机状态变量，ΔxDFIG为DFIG的状态变量，Δxzi为其他状态变量；ΔUN=[Δu1，Δθ1，Δu2，Δθ2, …，Δun，Δθn，Δm1,Δm2,…，Δmn]T，其中Δui，Δθi为网络节点电压幅值和角度增量；Δmi为网络中其他代数变量，ABCD为系数阵.

对公式(5)进行公式变换，能够得到

(6)

ΔUN(t)=-D-1CΔx=FΔx

，

(7)

公式中：Δx为状态变量；A′为n×n阶系统状态矩阵，系统小干扰稳定性由A′矩阵的特征值决定.

系统状态变量的解的一般形式为

(8)

公式中：φi，ψi分别为右、左特征向量，左右特征向量满足，当i=j时，φiψj=1，当i≠j时，φiψj=0.x0为系统状态变量的初始值.λi为系统特征值.

因此，系统输入矩阵可表示为

(9)

线路功率增量可表示为

ΔPij=uj 0Δui(Gijcosθij 0+Bijsinθij 0)+ui0Δuj(Gijcosθij 0+Bijsinθij 0)

+ui0uj 0Δθij(-Gijsinθij 0+Bijcosθij 0) .

(10)

转换成矩阵形式为

(11)

对公式(2)风机出口功率进行线性化，能够得到

(12)

系统中某支路模式势能函数和风机出口支路模式势能为[18]

(13)

(14)

公式中：ΔPwk为风机出口功率增量；Δθk为风机出口节点相角增量.

展开公式(13)和公式(14)的表达式，可知，含DFIG风电系统支路模式势能、风机出口模式势能由两部分构成，分别为

ΔVPij=ΔVPijz+ΔVPijh

，

(15)

ΔVPw=ΔVPwz+ΔVPwh

.

(16)

当系统只有一个主导模式时，自相关模式占主导，可重点分析自相关模式成分.互相关模式的影响另撰文分析，本文重点考虑自相关模式成分.

自相关模式，具体表达式为

(17)

风机出口支路自相关模式势能为

(18)

F=-D-1C，F=F(i，：)；n为系统状态矩阵阶数.

电力系统发生低频振荡时，存在不同振荡模式，由公式(17)和公式(18)可知，不同模式下支路振荡程度不同，支路振荡幅度越大，表明该支路越脆弱.因此，可根据支路势能第一次到达极大值时刻确定该模式下的脆弱支路，脆弱支路构成的割集可将系统“分割”成振荡趋势相反的两部分，即为某一模式下的振荡割集.

3 仿真及结果分析

电力系统中某一振荡模式下模式能量相互转化，模式势能在网络中也有所体现，不同支路分担的振荡能量不同，特别是风机接入电网后，影响网络中能量的分布，严重时将影响电网振荡割集能量的迁移与演变.为了详细分析支路模式势能与低频振荡的内在联系，本文采用电力系统分析软件(Power System Analysis Toolbox,PSAT)中WSCC3机9节点系统，其中，发电机均为二阶模型，DFIG采用五阶模型[21][vw，ωm，θp，idr，iqr]，分别研究DFIG替换和接入系统两种情况下电力系统小干扰稳定和模式振荡割集的影响，含DFIG并网的三机电力系统如图1所示.

系统不含风机时的特征值、阻尼比和振荡机群如表1中的风电渗透率为0所示，本文首先计算了不含双馈风机的支路模式势能分布情况，如图2所示.由图2可知，模式1中，支路{L98，L78，L96}在全网中振荡幅度较大，其中，支路{L98，L96}构成振荡割集，系统被划分为{G3}-{G1、G2 }，模式2中，支路{L75，L54，L96}在网络中振荡幅度较大，支路{L75，L96}构成振荡割集，系统被划分为{G1}-{G2，G3}，与小干扰分析结果一致.

表1 替换情况下不同渗透率下统振荡模式

渗透率/%模式特征根频率/Hz阻尼比参与因子01-1.966±j11.871.91540.1634机电振荡:{G3}-{G1,G2}2-0.7394±j6.781.08500.1085机电振荡:{G1}-{G2,G3}151-1.996±j13.62.18830.1452{G3,ωm,DFIG}-{G1,G2,idr,DFIG,iqr,DFIG }2-1.24±j9.031.45060.1356{G1,ωm,DFIG,iqr,DFIG}-{G2,G3,idr,DFIG}3-0.82±j1.570.28260.4618{ωm,DFIG}-{G1G2,G3,idr,DFIG,iqr,DFIG }301-2.53±j14.862.39870.1678{G1,G3,idr,DFIG}-{G2,ωm,DFIG,iqr,DFIG }2-2.01±j10.421.68870.1896{G1,ωm,DFIG,iqr,DFIG}-{G2,G3,idr,DFIG }3-0.82±j1.810.31690.4122{ωm,DFIG}-{G1G2,G3,idr,DFIG,iqr,DFIG }451-13.93±j24.144.43570.4998{G1,G3,ωm,DFIG,idr,DFIG}-{G2,iqr,DFIG }2-2.27±j11.821.91520.1884{G1,ωm,DFIG,iqr,DFIG}-{G2,G3,idr,DFIG }3-0.814±j2.080.35530.3646{ωm,DFIG}-{G1G2,G3,idr,DFIG,iqr,DFIG }

3.1 风机替换对系统振荡割集影响

在节点7接入DFIG，在增加风电渗透率的同时减少G2发电机的有功出力，使系统总有功出力保持不变，系统结构如图1所示.不同风电渗透率下特征值法计算结果如表1所示，由表1可知，风电渗透率从15%升到45%过程中，模式1的阻尼比呈现增大趋势；模式2中的阻尼比有着先增大后减小的趋势；双馈风机并网，系统新增一组振荡模式3，通过其振荡频率可知，该模式属于低频振荡领域范围，随着风电渗透率的增加，该模式下的阻尼比呈现下降趋势.由此可知，风机对不同模式下的阻尼比影响不同，需结合具体模式分析，利用特征值分析法能够得到发电机组间的阻尼比和振荡频率，但风机接入后，通过表1中的参与因子可知，不同模式下的阵型分布较为复杂，难以区分风机归属.

为此，本文利用支路模式势能分析了风电渗透率为15%，30%，45%下对系统振荡割集的影响.15%、30%、45%风电渗透率的支路模式势能分别如图3～图5所示.结合图3(a)、图4(a)、图5(a)可知，DFIG接入系统后，随着风电渗透率的增加，模式1中，支路势能衰减速度加快，振荡频率增加，支路势能振荡幅度逐渐增加；模式2中，支路势能衰减速度加快，振荡频率增加，各支路势能振荡幅度逐渐减小.由此可知，通过本文方法不仅能够清晰的反映出不同模式间的阻尼比和振荡频率情况，也能反映不同模式间支路振荡幅度大小.通过支路势能振荡情况可知，风电渗透率的增加改变了模式1的振荡割集，支路振荡割集从{L98，L96}迁移到{L75，L98}；风电渗透率的增加没有改变模式2中的振荡割集.由此可知，风电渗透率对不同模式影响不同.而通过本文方法，能够清楚的划分不同模式下的机群振荡情况，以模式1为例，15%风电渗透率时，振荡割集为{L98，L96}，系统被划分为{G3}{G1、G2、DFIG}两区域系统，30%风电渗透率时，振荡割集为{L98，L75}，系统被划分为{ G2、DFIG }-{G1、G3}，可知，利用本文方法，能够清楚的了解风电替换对系统振荡割集的影响，也可将风机接入系统后的振荡机群参与情况进行划分.

由表1可知，风机以替换同步机的形式接入电网，系统多增加了一组振荡模式3，本文从能量角度对该模式下的支路进行了能量解析，结合图3(c)、图4(c)、图5(c)可知，该模式下，风机出口支路模式势能最大，将{DFIG}与{G1，G2，G3}分为两个区域，但是，风机出口支路的模式势能随着风电渗透比的增加呈现不断减小的趋势，而网络中支路的势能呈现上升趋势，由此可知，模式3中，风机出口支路模式势能与网络中的支路模式势能存在着能量迁移现象.为了能够更加清楚的了解该模式下能量的交互，仿真分析了60%和75%风电渗透率的支路势能分布情况，如图6所示.由图6可知，随着风电渗透比的增加，模式3的脆弱支路发生了改变.

3.2 风电接入对系统振荡割集影响

为深入分析风电接入电网的影响，在9节点接入DFIG，系统结构如图1所示.首先利用特征值分析法对接入不同出力的DFIG风机进行分析，小干扰特征值结果如表2所示.由表2可知，风机接入系统后，系统振荡频率增加，模式1和模式2的阻尼比均低于系统的原有阻尼比，系统新增一组振荡模式3，该模式的阻尼比随着风电渗透率的增加呈现下降趋势，由此可见，风机接入对系统不同模式影响不同.

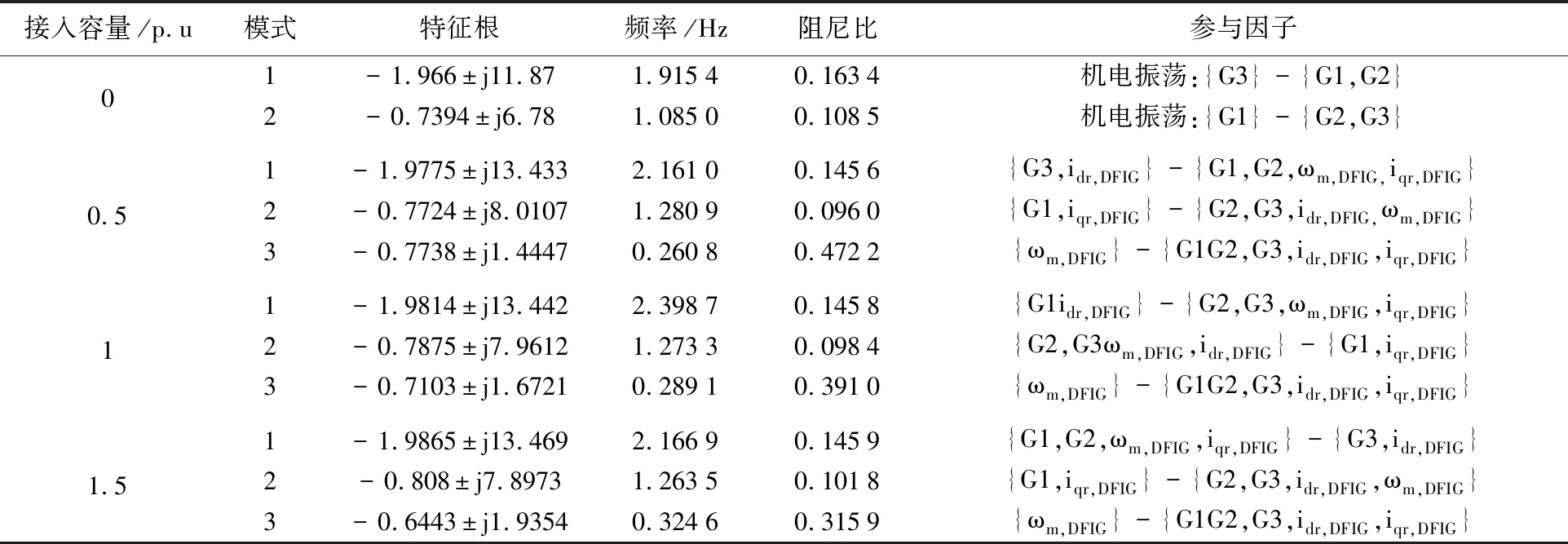
表2 接入情况下不同容量DFIG系统振荡模式

同样，利用本文方法分析风电接入后对支路模式势能的影响，不同接入容量的支路模式势能如图7～图9所示，从图7(a)、图7(b)，图8(a)、图8(b)，图9(a)、图9(b)可知，随着风电渗透比的增加，结合图1可知，模式1中由脆弱支路{L98，L96}构成的振荡割集和模式2中的振荡割集{L75，L96}均没有发生改变，但随风电渗透比的增加，模式1和2的振荡割集的振幅均有增大趋势.

对于新增的振荡模式3，本文利用支路模式势能对其分析，从图7(c)、图8(c)和图9(c)可知，该模式下风机出口模式势能最大，将{DFIG}与{G1，G2，G3}分为两区域，且网络中各支路势能随着风电渗透率的增加而增加，而风机出口支路模式势能呈现减小趋势.

4 结 论

本文以WSCC3机9节点算例为研究对象，通过支路模式势能函数，从网络角度研究了DFIG接入和替换对系统自相关支路模式势能及振荡割集的影响，并得到如下结论：

(1)DFIG以替换的形式接入电网系统增加一个振荡模式，该模式下支路振荡幅度均大于模式1和模式2下的支路振荡幅度，为系统的主导振荡模式，风电的渗透率增加会改变模式1和模式3的振荡割集分布；

(2)DFIG直接接入电网，系统新增一组振荡模式，该模式下的支路势能振荡幅度均大于模式1和模式2下的支路势能振荡幅度，为系统的主导振荡模式，风电的渗透率增加不改变模式1和模式2的振荡割集，新增模式3的支路模式势能随着渗透率的增加而增加，风电出口支路模式势能呈现减小趋势.

(3)通过本文方法确定的振荡割集，可给出不同模式下的含风机的振荡分群情况.