基于原子稀疏分解和支持向量机的风电功率实时预测研究

杨 茂，刘慧宇，孙 勇，李宝聚

(1.现代电力系统仿真控制与绿色电能新技术吉林省重点实验室(东北电力大学)，吉林 吉林 132012；2.国网吉林省电力有限公司，吉林 长春 130000)

由于环境污染问题日益严重，风能作为一种可再生的清洁能源，越来越受到世界各国的青睐[1].风力发电已成为很多国家重点发展的可再生能源之一，我国风电年装机容量成倍增长，至2018年底，中国累计风电装机容量192 250兆瓦，较2017年新增装机23 015兆瓦.我国已成为世界装机容量最大的国家.随着风电装机容量逐年递增，风电功率本身的的波动特性以及非平稳特性成为阻碍风电大规模并网运行的难题[2-4].寻求更有效的预测模型进行风电功率实时预测是实现风能大规模并网及合理调度的有效手段之一.

2011年国家能源局《关于印发风电场功率预测预报管理暂行办法的通知》[5](国能新能〔2011〕177号)中指出：风电功率预报分日预报和实时预报两种方式，日预报是指对次日0时至24时的预测预报，实时预报是指自上报时刻起未来15分钟至4小时的预测预报，时间分辨率为15分钟.因此需要对风电功率实时预测方法进行深入的研究.

国内外现有的风电功率预测方法按预测模型可以分成三类，即物理方法，统计方法和组合预测方法.物理方法利用数值天气预报(NWP)模型，并考虑风机物理因素，通过已建立的风速与风电功率的统计模型进行风电功率预测.由于NWP模型需要较长时间操作和大量的计算数据，且在我国很难获得数值天气预报，因此物理方法不适用于短期预测.统计方法不考虑气象信息，只应用风速、风电功率数据序列便可进行建模预测，文献[6]给出了常用的统计方法：自回归滑动平均 (ARMA) 方法，差分自回归滑动平均(ARIMA)模型和支持向量机 (SVM)模型等.ARMA和ARIMA模型适合线性时间序列的预测，不适合具有非线性特点的超短期风电功率时间序列.文献[7]介绍了支持向量机模型，该模型能非常成功进行时间序列分析，适合解决非线性问题.整合上述单一预测模型得到改进的预测模型称为组合模型.文献[8]给出了基于时间序列多采样尺度的组合预测方法，文献[9]介绍了基于小波分解的组合预测方法，文献[10]给出了基于动态权重的组合预测方法.

超短期原始风电功率序列具有非平稳性，SVM是一种广泛应用的风电功率预测方法，但它训练时间较长，往往不能完全映射风电功率的非平稳特性.原子稀疏分解(Atomic Sparse Decomposition,ASD)具有强非平稳信号跟踪及预测的能力，能很好的映射风电功率的非平稳特性.将ASD作为SVM的前置分解手段，可以弥补SVM在预测中的不足.非平稳的超短期原始风电功率序列，可以看做是多个原子分量和残差分量的叠加，其非平稳性导致原子参数不断变化.对原子分量进行自预测，残差分量进行SVM预测，将预测结果叠加得到最终的风电功率预测值.算例结果表明，与常规的SVM方法相比，将ASD作为SVM的前置分解进行组合预测，可以显著提高风电功率预测精度.

1 原子稀疏分解理论

近年来，寻求信号的稀疏表示已成为信号处理领域的研究热点之一.稀疏分解理论认为，分解的结果越稀疏则越接近信号的本身的内在结构.ASD采取贪婪的自适应分解策略，其原子字典(原子库)是过完备[11](高度冗余)的，任何信号都可以用其中的一组最佳原子来表示，所用的原子数越少，分解结果越稀疏.

1.1 构造原子字典

在原子稀疏分解中，原子通常由一般性的核函数表示，如：Chirp函数，δ函数和复正弦函数.本文选用的Gauss函数为

(1)

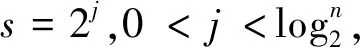
1.2 双字典集的分解算法

稀疏分解理论认为，分解的结果越稀疏则越接近信号的本身的内在结构.从原子的角度看，就是选用的原子数目越少，分解结果越稀疏.分解的过程就是不断迭代选取最优原子的过程，在迭代过程中，过完备原子字典中的原子可分为两类，一类为已被选过的旧原子，一类为未被选过的新原子[13].将已被选过的原子放进已选字典集Dold，未被选过的原子放进待选字典集Dnew，从稀疏性的角度看，在进行下一步迭代时，选用新原子不利于分解结果的稀疏性，因此应尽可能的从Dold中选用旧原子.最优原子[14-15]选取流程如下.

输入风电功率时间序列x(t)，根据序列长度确定高斯核函数的中心因子和尺度因子，形成由高斯核函数组成的过完备原子库.原子库包含两个字典集：已选字典集Dold和待选字典集Dnew，此时所有原子都在Dnew中，残差r0(t)=x(t).

(1)计算残差信号与已选字典集中所有原子的内积〈r0(t)，Dold〉，选出最大内积Iold及其对应的Dold中的原子aold，计算残差信号与待选字典集中所有原子的内积〈r0(t)，Dnew〉，选出最大内积Inew及其对应的Dnew中的原子anew.

(2)如果|Iold|≥|Inew|，选取aold作为最优原子，即aopt1=aold，Iold作为该最优原子的迭代系数，更新残差信号r1(t)=r0(t)-Ioldaold.

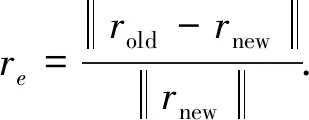
(4)返回第一步，分别计算r1(t)与两个字典集中所有原子的内积，重复上述步骤，直到第n次迭代所得残差rn(t)满足最小残差约束条件，终止迭代.

此时原始风电功率时间序列为

(2)

双原子字典原子稀疏分解流程图，如图1所示.

2 ASD-SVM组合预测模型

本文的超短期风电功率多步组合预测方法如图2所示.预测步骤如下：

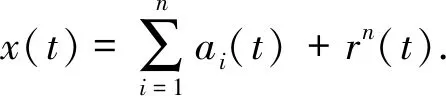
(2)根据ASD表达式自预测当前时刻下，后16个时刻的原子分量值.

(3)将残差分量输入SVM预测模型，得到当前时刻下的后16个时刻残差预测值.

(4)将ASD预测结果与SVM预测结果对应时刻叠加，得到当前时刻下风电功率16步预测结果.即

(3)

3 算例分析

3.1 算例一

以吉林省某风电场为例，该风电场装机容量为265.5MW.数据采样的时间段为2014年8月1日至2014年8月10日，采样数据为风电场总功率，本文采用的是经过处理的间隔15 min的数据，共960个点，选取前300个点作为数据样本.选取前250个点作为训练样本数据输入ASD模型，取这250个点的ASD残差分量数据输入SVM模型进行训练，得到SVM预测模型.选取后50个点作为预测样本，输入ASD-SVM模型进行预测.第275点SVM残差16步预测结果曲线图如图3所示，从图3中可以看出，SVM模型可以很好地跟踪预测残差分量的走势，证明SVM适合预测能量相对较小的残差信号.

第275点ASD-SVM、SVM16步预测结果与实际功率对比曲线图如图4所示.从图4中可以看出，ASD-SVM模型预测结果的曲线走势更接近于实际功率曲线，即本文方法预测效果更好.

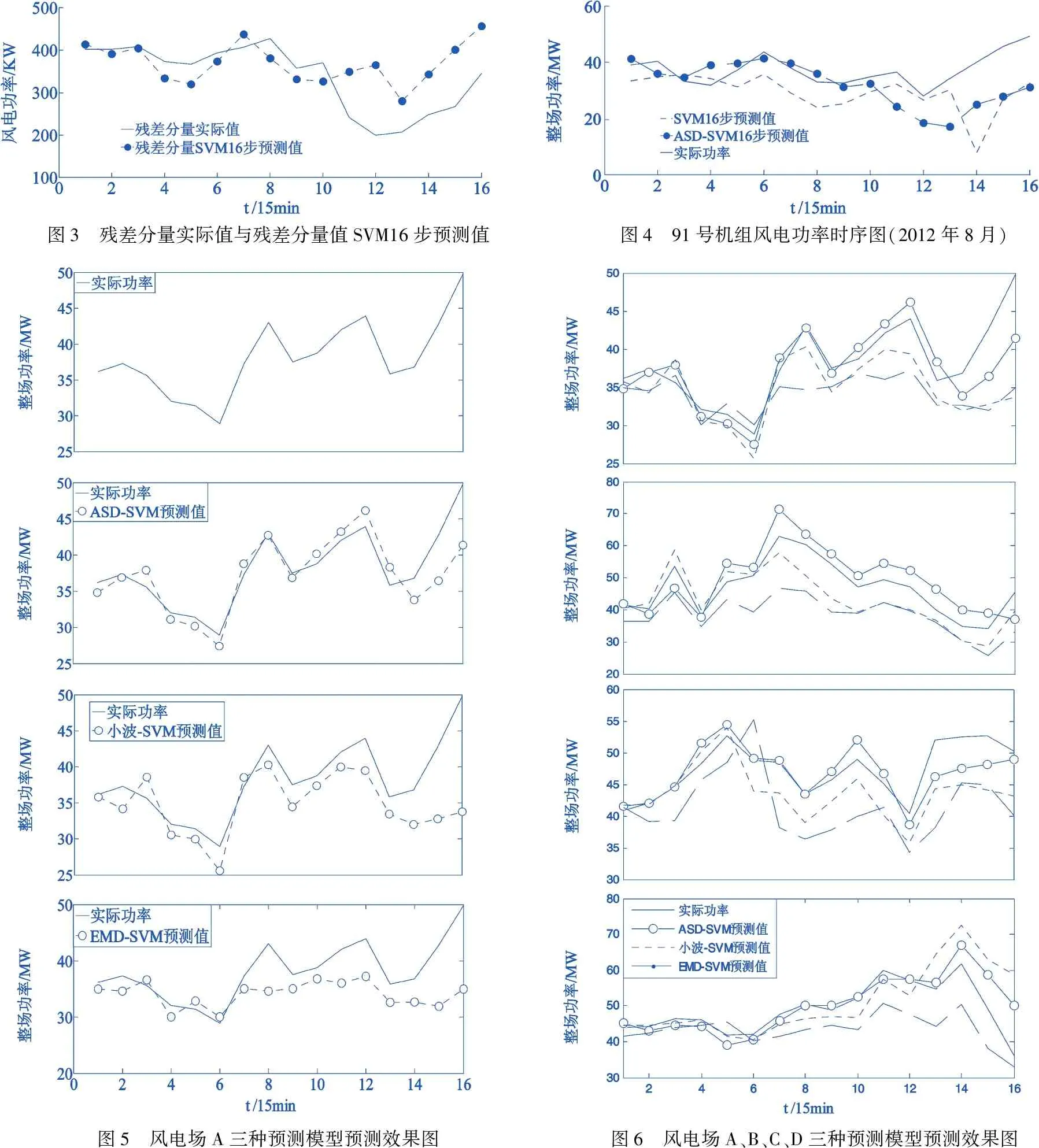
图3 残差分量实际值与残差分量值SVM16步预测值图4 91号机组风电功率时序图(2012年8月)图5 风电场A三种预测模型预测效果图图6 风电场A、B、C、D三种预测模型预测效果图

3.2 算例二

以吉林省A、B、C、D四个风电场为例，数据采样的时间段和时间间隔不变，采样数据共960个点，选取前300个点作为数据样本.选取前250个点作为训练样本数据分别输入ASD-SVM模型，小波-SVM模型和EMD-SVM模型进行预测.

风电场A数据样本第275点的三种预测模型预测效果图，如图5所示.可以看出，ASD-SVM模型的预测曲线(第二张图)更贴近实际功率曲线，即：ASD-SVM模型具有更好的预测效果.

利用三种预测模型对A、B、C、D四个风电场数据样本的第275点进行预测所得的预测效果图，如图6所示.其中：实线为实际功率曲线，带圈实线为ASD-SVM模型预测曲线，点线为小波-SVM模型预测曲线，虚线为EMD-SVM模型预测曲线，四个图型由上至下依次为ABCD四个风电场的三种模型预测结果.可以看出，带圈实线最接近实线，即本文提出的ASD-SVM模型预测效果比基于小波和基于EMD的模型预测效果好.

3.3 评价指标

(1)全天预测结果均方根误差

(4)

(2)日平均预测计划曲线准确率

(5)

(3)日平均预测计划曲线合格率

(6)

(7)

指标全天预测结果均方根误差εDRMSE越小，日平均预测计划曲线准确率rzq和日平均预测计划曲线合格率rhg越大，预测效果越好.算例一预测结果三项指标统计结果如表1所示.根据表中结果可以看出，ASD-SVM方法较之SVM模型，日均方根误差εDRMSE降低了7.06%，日平均预测计划曲线准确率rzq提高8.68%，日平均预测计划曲线合格率rhg提高了12.08%.说明将ASD作为SVM的前置分解手段进行组合预测，可以提高超短期风电功率多步预测精度，验证了ASD-SVM预测模型的有效性.

表1 ASD-SVM和SVM模型预测结果

算例二预测结果三项指标及模型运行时间统计结果，如表2所示.根据表中结果可以看出，ASD-SVM方法较之小波-SVM模型，εDRMSE平均降低了5.15%，rzq和rhg分别平均提高2.9%和4.12%.运行时间平均缩短15.60 min.ASD-SVM方法较之EMD-SVM模型，εDRMSE平均降低了8.68%，rzq和rhg分别平均提高7.39%和7.05%，运行时间平均缩短22.95 min.说明本文提出的ASD-SVM模型比基于小波和基于EMD方法的模型预测精度都高，且耗时更短，计算效率更高.这是由于ASD方法分解所得原子分量进行自预测，只需多迭代一次，只有一个残差分量需要输入SVM预测模型进行预测，而另两种方法所得全部分量都需要输入SVM预测模型进行预测.这大大减少了ASD-SVM方法中SVM模型的训练量，以及分量的预测时间，提高了模型的计算效率.

表2 EMD-SVM、小波-SVM和ASD-SVM模型预测结果

表2中三种预测模型在四个风电场的预测结果的三个评价指标曲线图，如图7所示.由图7可以直观的看出，本文提出的ASD-SVM具有更好的预测效果.

6 结 论

本文针对超短期风电功率多步预测问题提出一种ASD-SVM组合预测方法，利用ASD对原始风电功率序列进行分解，得到原子分量和残差分量.对原子分量进行自预测，残差分量进行SVM预测，预测结果叠加得到最终的超短期风电功率16步预测值.用风电场的实时风电功率数据进行验证，结论如下：

(1)相较于传统的SVM模型，ASD-SVM模型使得风电功率日平均预测计划曲线的准确率及合格率分别提高了8.68%和12.08%，风电功率日均方根误差降低了7.06%，即ASD-SVM模型预测效果更好.

(2)通过四个风电场的验证分析得知，ASD-SVM模型比基于小波的SVM模型和基于EMD的SVM模型具有更高的预测精度且耗时更少.因此，ASD-SVM模型更适合进行超短期风电功率实时预测.

(3)由于超短期风电功率时间序列是不断变化的，而本文所用原子稀疏分解的原子库却是固定不变的，这不利于ASD的稀疏分解，应该根据变化的风电功率时间序列实时更新原子库.这也是本文今后要努力研究的问题.