Matlab在光孤子教学中的应用

成纯富 欧艺文 陈嘉轩 陈文嘉

【摘 要】Matlab仿真具有编程简单、绘图功能强大，仿真结果形象直观等优点，在辅助教学中发挥着越来越重要的作用。本文探讨将Matlab仿真引入光孤子的辅助教学中，并阐述了其具体的实现过程。结果表明，Matlab仿真教学不但可使课程中晦涩难懂的内容变得直观、易于理解，而且还可激发学生的学习兴趣，提高学生的创新能力和课堂教学效果。

【关键词】光纤通信系统;Matlab;光孤子

【中图分类号】G642  【文献标识码】A  【文章编号】1671-8437（2020）34-0001-02

光纤通信系统课程是光学工程专业一门重要的核心课[1]，也是一门多学科交叉渗透的专业课，具有内容繁杂、理论性强等特点。故光学工程专业的学生要学好该课程，不但要具有一定的光学专业基础，还必须具有一定的电学、数学等专业基础。由于该课程对学生要求高，传统教学又枯燥乏味，所以需要创新该课程的教学，激发学生的学习兴趣。Matlab仿真辅助教学由于具有直观、简单易学等优点[2-3]，已在光纤通信系统课程的光纤模式和传输原理实验教学中取得了很好的教学效果[4，5]，但到目前为止，光孤子的Matlab仿真辅助教学应用不足。为此，本文探究将Matlab仿真引入光纤通信系统课程的光孤子辅助教学中，以期提高学生的学习兴趣和改善教学效果。

1   Matlab在光孤子教学中的应用

根据光孤子理论可知，孤子是一种在传输过程中形状保持不变的光脉冲，其产生机理是群速度色散效应和自相位调制效应的精确平衡，故描述光孤子传输特性的方程为

（1）

（1）式中，A为光脉冲振幅，β2为光纤的二阶色散系数，γ为非线性系数。方程（1）中左边第二项描述群速度色散效应，右边那一项描述自相位调制效应。

方程（1）通常采用分步的傅里叶方法进行数值求解，核心思想：当传播距离的步长较短时，光纤的色散效应和光纤的非线性效应在传输过程中可分别独立作用。为阐述分步傅立叶方法的基本原理，方程（1）可改

写为

（2）

（2）式中，代表光纤的色散项，代表光纤的非线性项。

当步长较小时，采用分步傅立叶方法，假设第一步仅有色散效应作用，且通过傅里叶变换将方程（1）变换到频域求解，则方程（2）变为

（3）

假设下一步仅有非线性效应作用，且通过傅里叶逆变换将方程（3）计算的结果变换回时域进行求解，则方程（2）变为

（4）

为了提高分步傅立叶方法的计算精度，一般采用对称分步傅立叶方法进行数值求解。该数值求解方法是先让半个步长中色散效应起作用，然后在下一全步长中让非线性效应起作用，再在下半个传输距离步长中让色散效应起作用。

在群速度色散和自相位调制效应的相互作用下，在光纤中可形成阶孤子，其大小可表示为

（5）

（5）式中，为色散长度，其大小决定着光纤色散效应的强弱。为非线性长度，决定着非线性效应的强弱。

当时，群速度色散效应和自相位调制效应达到精确平衡，从而形成一阶光孤子，即脉冲现状不随传输距离的变化而变化。当时，光纤中将形成高阶孤子，高阶孤子脉冲受群速度色散效应的影响而分裂成个基孤子，且其频谱和时域形状呈现出周期性的变化，其演变周期为

（6）

基于上述光孤子理论，可编写Matlab程序，其核心代码如下。

N=2^10;            % 傅里叶变换采样点数

Tr=12000;        % 時间范围

dt=Tr/N;           % 时间间隔

dw=2*pi/（N*dt）;   % 频率间隔

T=（（1：N）-（N/2））*dt;% 时间数组

w=（（1：N）-（N/2））*dw;% 频率数组

a=0;             % 光纤传输损耗

g=1.3d-3;         % 非线性系数 [1/W/m]

B2=-20d-3;         % 二阶色散系数. （ps^2/m）

T0=18;             % 初始脉宽 （ps）

Nm=1;              % 孤子阶数

LD=（（T0^2）/（abs（B2）））;   % 色散长度 [m]

Lnl=LD/Nm^2;           % 非线性长度

P0=1/（Lnl*g）;          % 入射峰值功率 （W）

dz=60;                % 传播距离步长 [m]

z0=（pi/2）*LD;          % 孤子传输周期 [m]

z=（0：dz：z0）;         % 传输距离数组 [m]

Et=sqrt（P0）*sech（T/T0）; % 时域振幅

It（1，：）=abs（Et）.^2;     % 时域强度

Aw=fftshift（fft（Et））;   % 频域振幅

Iw（1，：）=abs（Aw）.^2;      % 频域强度

m=length（z）;

for j=1：m-1

Aw=Aw.*exp（-a*（dz/2）-1i*B2/2*w.^2*（dz/2））;

Et=ifft（Aw）;

Et=Et.*exp（1i*g*（（abs（Et））.^2）*（dz））;

Aw=fft（Et）;

Aw=Aw.*exp（-a*（dz/2）-1i*B2/2*w.^2*（dz/2））;

Et=ifft（Aw）;

It（j+1，：）=abs（Et）.^2;

Iw（j+1，：）=abs（Aw）.^2;

end

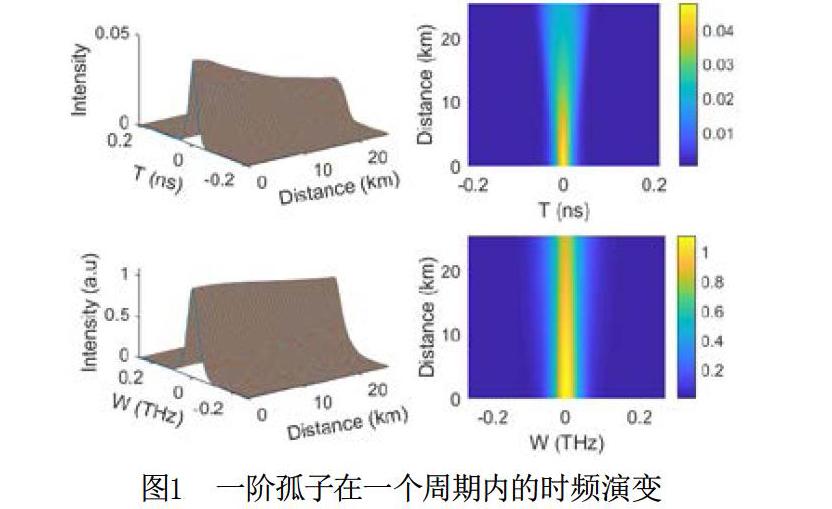
利用上述核心代码，可得到如图1所示的仿真结果。其中，图1上半部分为时域演变图，下半部分为频域演变图。为便于学生多角度观察演变规律，分别用plot3和pcolor画出了三维演变图。由图1可以看出，一阶孤子脉冲受光线群速度色散效应和自相位调制效应的相互作用，仍然保持脉冲现状不变的传输，仿真结果与理论结果一致。增大入纤峰值功率时，光纤中將形成高阶孤子，高阶孤子受色散效应的影响而产生分裂现象。利用上述程序，学生不但可以很直观地看到孤子脉冲的演变规律，而且可以深入理解分布的傅里叶数组求解方法以及快速傅里叶变换等函数的调用方法。当然，学生在深入理解上述Matlab代码后，对相关的孤子理论也会有更深入的理解。此外，在上述核心代码的基础上，学生可以适当改写或补充程序，实现光脉冲（如高斯脉冲、双曲正割等）在特种光纤（如光子晶体光纤、中红外单模光纤等）中的传播特性。所以，基于Matlab的仿真辅助教学可以提高学生的创新能力。

2   结论

本文探究了将Matlab仿真引入到光纤通信系统课程的光孤子辅助教学中，并给出了核心代码来阐述其具体的实现过程。实现仿真结果三维可视化，有助于学生深度理解光孤子理论;仿真代码具有易理解和可拓展的特点，可显著提高学生的创新能力。因此，Matlab仿真辅助课堂教学可显著提高学生的学习兴趣和教师的教学

效果。

【参考文献】

[1]沈建华，陈健，李履信编著.光纤通信系统（第3版）[M].北京：机械工业出版社，2014.

[2]张学敏，倪虹霞编著.Matlab基础及应用（第二版）[M].北京：中国电力出版社，2012.

[3]李茜.辅助教学平台在“光纤通信”课程中的应用[J].唐山学院学报，2014（27）.

[4]陈明阳.MATLAB在光纤通信课程教学中的应用[J].计算机教育，2006（12）.

[5]何伟刚，吴其琦.Matlab仿真在光纤通信实验教学难点中的应用[J].实验室研究与探索，2013（32）.

【作者简介】

成纯富（1976～），男，湖北阳新人，博士，湖北工业大学副教授。研究方向：FPGA开发与设计。