建模思想在《Petri网理论与应用》教学中的渗透

王丽丽 方贤文

摘要：文章阐述了《Petri网理论与应用》的教学目的和性质，指出了传统教学方法及手段的弊端，说明了在课堂教学中引入建模思想的必要性和重要性。将建模思想贯穿于课程教学过程中，是提高学生的知识综合运用能力、培养学生发现问题-分析问题-解决问题的能力的必然举措。通过实例详細讲解了建模思想在实际问题的求解中的应用，通过建模思想的渗透有效地改善了教学效果，提高了学生实践能力。

关键词：Petri网; 建模思想; 教学研究;实际应用

中图分类号： G642       文献标识码：A

文章编号：1009-3044（2020）35-0146-03

开放科学（资源服务）标识码（OSID）：

The Penetration of Modeling Thought in the Teaching of " Petri Net Theory and Application"

WANG Li-li，FANG Xian-wen

（School of Mathematics and Big Data， Anhui University of Science and Technology， Huainan 232001 China）

Abstract： The paper elaborates the teaching purposes and its features of “The theory and application of Petri net”， and points out the disadvantages of traditional teaching methods， emphasizing the necessity and importance of introducing modeling ideas into classroom teaching. It is a necessary measure to merge modeling idea into course teaching in order to enhance students abilities of applying theory into reality and train students ability of finding， analyzing and solving problems. The application of modeling ideas in solving practical problems is detailed by some examples. The introduction of modeling idea effectively improves teaching effects and students practical ability.

Key words： Petri Nets; modeling idea; teaching research; practical application

Petri网于1962年首次被德国的Carl Adam Petri 在其博士论文“Communication with Automata”中提出，其主要应用于分布式系统的建模与分析，特别适合描述冲突和并发关系[1]。目前Petri网已经形成了一套完整的理论体系，成为一门系统的、独立的学科分支，并在各大领域得到了广泛的应用。

Petri网是既有直观的图形表示，也可以引入数学方法对其性质进行分析。它既可以用于系统的静态结构分析，也可以用于动态行为分析[2]。Petri网的理论是建立在严格的数学基础上，由于其理论研究已经比较完善，而且有些性质理论证明相对比较复杂，在指导学生学习这门课程时，除了掌握其特征和性质之外，更多的是培养学生活学活用的能力，学会将Petri网作为工具来对现实生活中的问题进行建模，从而分析出动态和静态的性质。学习此门课程的侧重点是培养学生的建模思想和发现问题-分析问题-解决问题的能力。很多同学在学习《Petri网理论与应用》这门课程时，学习的目标不明确，导致过多地关注在其各种性质和分析方法的理论证明上，造成了学生对这门课程的学习日益产生了畏惧的情绪，学完以后不知道Petri网能干什么以及为什么要学习这门课程，无法理解课程的精髓，建出的模型也是错误百出，从而失去了开此门课程的真正意义。

因此，对《Petri网理论与应用》的教学方法及手段做出调整是势在必行。本文简单地阐述了如何将建模思想贯穿于《Petri网理论与应用》教学中，倡导新的教学思路和教学手段使得此门课程的讲授焕发崭新的生命力，从而实现较好的课堂教学效果。

1 明确课程性质和教学目的

《Petri网理论与应用》是部分计算机专业硕士培养的专业选修课。对于不是专门从事Petri的理论研究的学生，一般只需要掌握其基本概念，动态性质和结构性质，以及动态性质的分析。如Petri网的运算，并发论和同步距离部分可以作为选修内容。为了更好地将Petri网应用于实际系统的建模，除了掌握原网之外，更多的是使用它的一些变形网结构，其语义表达能力比原网要丰富很多。因此学时允许的条件下，应该指导学习进一步了解一些高级Petri网，如颜色Petri网、谓词/变迁网系统、时间Petri网、时延Petri网、连续Petri网、模糊Petri网等。

针对大部分专业和学生来说，开设此门课程的最终目的是掌握Petri网的应用能力，而不是侧重理论研究。所以从一开始讲授这门课程时就需要将建模的思想融入教学中，不能偏离应用主线，不能仅拘泥于理论教学，需将理论与实践相结合，重点培养学生的综合运用能力，将Petri网变为一种“武器”来帮助解决实际生活中出现的问题。所以教会学生如何更好地使用该“武器”，比盲目地研究“武器”是如何制造显得更加重要。

2 建模思想贯穿教学始终

2.1  建模思想融入课堂教学

学习《Petri网理论与应用》旨在使用它解决实际问题，将建模思想充分渗透到课程教学中是必然举措。理解基本概念之后，教师应潜移默化通过案例的引入带领学生如何进行建模，进一步巩固理论知识的综合运用，起到举一反三的作用。Petri网与物理学和化学等学科不同，它不直接描述自然的规律本身，只描述由这种规律产生的依赖关系。

首先，洞察实际问题是否适合用Petri网建模。

Petri网最大的贡献不仅仅是为我们提供了既有图形又有形式化定义的模型，更重要的是它通过这些模型发掘出来的原理和概念，使得我们能更准确地把握和分析应用问题，从而找到解决问题的关键。但Petri并不是万能的，不是任何应用问题都适合用它建模和分析。网系统的最大行为特征是资源能沿着有向弧流动。这种流动不全是物理意义上的流动，如状态，性质及数量等，与地理位置无关的一种改变[2]。认清应用问题中的变化是否有流动的特征，再决定Petri网是否适合作为分析工具。

其次，围绕目的进行建模。

适用于Petri网的实例有生产流水线、业务流程分析、化学反应、电梯控制系统等。有些具有明确的变化目标，有些是自然呈现出规律[2]。不管系统本身有没有目的性，人为建模是要有明确目的。所以，无论何时采用Petri网，在建模前一定要确定建模的目的，然后根据目的确定观察对象，找出哪些是库所，哪些是变迁，有向弧该如何流向，以及是否需要有权函数和容量函数。

最后，建模思想成为主力军。

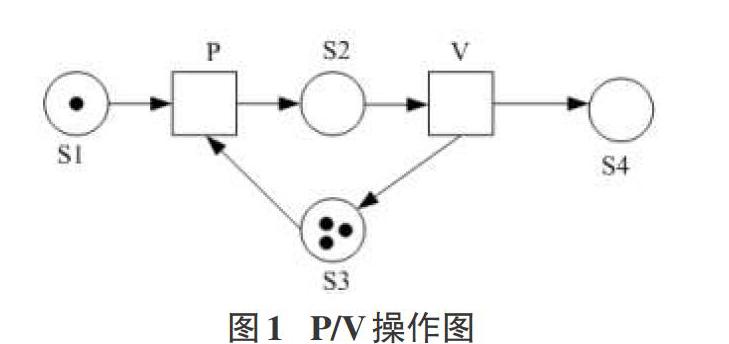
在实际应用中，Petri通常被用来描述可观察的对象，这些对象能呈现有规律的定性或定量的改变。这种可观察的对象在Petri中称为资源，并且用库所表示。库所中的tokens数量表示资源的数量。资源的改变通过变迁的引发产生，变迁可以表示一系列的动作。每个变迁的发生会有一个前因导致并产生一个后果，前因和后果分别表现为消耗和产生的效果，因此在网系统中的体现为变迁前集库所和后集库所中的tokens的变化。如操作系统中的PV操作，P操作使信号量的值减1，V操作使得信号量的值加1，且信号量的值为非负时，P操作才能进行[1]。那么P/V操作的Petri网模型中，将P和V两个操作表示为变迁（因为它是动作），信号量表示为库所（因为是资源），又因为已知只有信号量为正数时P操作才能进行且会导致信号量值减1，故此时信号量库所必然后P变迁的前集，同理推导出为V的后集。从而可以得到图1所示的Petri网模型。该模型中的P、V变迁分别表示P、V操作，S3表示信号量资源，里面的tokens表示资源的数量。S2是为了保证系统的正常运行人为添加的一个控制库所，控制P和V操作可以循环执行。S1和S4是提供对外的两个接口库所。通过逐层剖析，很容易就得到了如下模型。

2.2 建模思想融入课后练习

课后练习是课堂教学的延伸和巩固，教师在布置课后作业的时候，一改传统的死板的做证明和理论知识的习题模式[3，4]，而应设计一些实际问题，引导学生学以致用，将Petri网用于实际问题的建模和分析，从而更好地提高学生理论联系实际的能力，提升学生的专业综合素质。如让学生对网络购票、酒店预定、交易支付、学生选课、学生评教等系统进行建模，并形成一份课后完整的实验报告，分析系统中的存在的问题。

3 建模思想的实际应用

问题的描述：5 个哲学家坐在一个圆桌旁，圆桌上摆满了中餐食品，每两个哲学家之间摆了一根筷子。一个哲学家要吃食品时，必须同时拿起他左边的和右边的筷子。这时坐在他旁边的两位哲学家就不可能有足够的筷子来吃食品，只能坐在那里思考问题[1]。每位哲学家从“思考”状态进入“吃食品”状态的条件是在他左、右两边的两根筷子未被使用。试图通过Petri网模型对其进行建模。

为了避免出现饥饿死循环状态，这个模型已对问题进行了一定的处理：规定只有当位于一个哲学家左右两根筷子都未被占用时，他才能拿起筷子（而且同时拿两根筷子）。这就避免出现：每位哲学家都拿起一根（譬如说右边的一根）筷子不放下，等待别人让步，而结果谁也吃不上。

显然这个问题存在状态转换，各个事件的发生存在依赖关系，可以使用Petri网对其进行建模，为了说明如何将建模的思想应用到这个实例中，这里只给出最简单的一种Petri网模型。

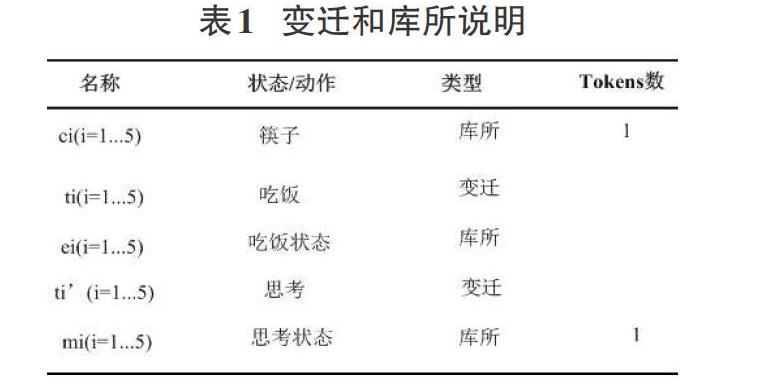
问题的分析：本问题中的资源只有筷子;哲学家有两种状态：吃饭和思考状态;动作有吃饭和思考两种;筷子在五位哲学家竞争使用，吃饭和思考状态存在交替流向关系。根据问题的描述在建模时可以抽象出表1所示的变迁和库所。

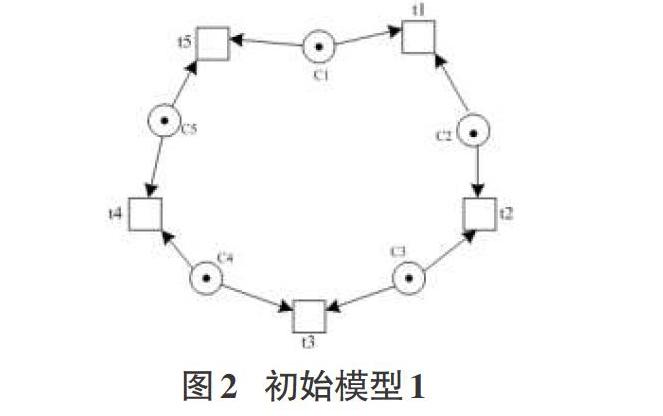
随后，构建上述变迁和库所之间的流关系，由于每根筷子供两边的哲学家使用，哲学家只有位于两边的筷子都未被使用（即含有tokens时）才能进餐吃饭，从而轻而易举就可以得出图2所示的初始的模型1;在模型1的基础上，当哲学家得到筷子就發生吃饭动作ti，同时进入吃饭状态ei，吃完了以后，继而又进入思考状态ti，思考时，每个哲学家需要将占用的两个资源筷子释放掉，从而产生了弧，从而得到图3所示的模型2;再仔细思考，我们会发现在模型2中忽略了思考状态，从而进一步剖析，如果需要进餐，说明当前的哲学家一定是处于思考状态，从而产生了弧，一旦发生了ti，哲学家也就再次进入思考状态，等待下次进餐。继而又产生了弧，最终得到图4所示完整模型3。

通过实例的分析，不难发现，在实际建模时，首先我们要根据目的抽象出变迁和库所，然后找出它们之间的流向关系，以及初始状态时库所中的tokens的分布情况。对于十分复杂的系统，可以采用分层建模，局部求精的方法。和软件开发的思想是一样，首先构建系统的顶层模型，然后再局部细化。利用Petri网对实际问题建立出正确的模型，不是一朝一夕的事情，需要在教学中适当引导，大量的实践。

4 总结

在《Petri理论与应用》教学中融入建模思想，是达到这门课程教学目的的必然举措，建模思想在《Petri理论与应用》的教学过程中起到举足轻重的作用。通过建模来提高学生对知识的迁移能力和应用能力，为他们今后解决实际问题提供知识应用技能[5]。本文围绕课程教学中建模思想的培养展开讨论，很大的丰富了教学方法和手段，优化了教学效果。

参考文献：

[1] 吴哲辉.Petri网导论[M].北京：机械工业出版社，2006.

[2] 袁崇义.Petri网应用[M].北京：科学出版社，2013.

[3] 赵瑞，曹靖.将数学建模思想融入工科数学教学[J].教育与职业，2016（10）：119-120.

[4] 郭欣.融入数学建模思想的高等数学教学研究[J].科技创新导报，2012，9（30）：165-166.

[5] 高国继.建模思想在高职数学课堂教学中的有效实践[J].西部素质教育，2016，2（24）：100.

【通联编辑：唐一东】