快链条模型下落运动的探究

李恩溢 高 博 金伟秋 盛裕杰

(西安交通大学 1理学院，大学物理国家级实验教学示范中心；2电气学工程学院，陕西 西安 710049)

在传统的下落链条的力学模型[1]中，认为从一定高度释放的链条的各部分均做自由落体运动，即认为链条各部分间不存在拉力。该模型对一般概念下的链条有很好的解释效果，但若拓宽对链条的定义，那么只要构造的链条足够特殊则传统的链条模型将不再适用。

目前，国外已有一些研究表明了这一点：R.H.Plaut等人发现一种特殊构造的链条，其下落快于自由落体，从而得出下落时链条悬空部分存在拉力的结论[2]，并称这类链条为快链条。Rod Cross等人通过研究不同的几何形状的物体落地时的能量耗散，得出了一定条件下刚性杆落地后杆的机械能不守恒的结论[3]。Anoop Grewal等人亦通过理论分析给出了几种下落速度快于自由落体的链条模型[4]。

但目前国外文献对快链条下落过程进行数学描述和计算时，一般采用连续模型对整段链条的下落过程进行描述，即认为快链条在下落过程中速度是连续变化的，而实际上，快链条在下落过程中运动的模式是反复切换的，速度变化曲线也存在跳跃间断。因此，为补充已有研究的不足，本文将针对一种典型结构的快链条，对其下落过程的各个阶段展开分析，以得出描述快链条下落的一般方程，并通过实验验证该模型的合理性。

1 快链条下落过程的定性分析

本节定性分析快链条的下落过程，通过证明快链条落地后存在局部的速度突增，说明链条下落时，连接绳将绷紧而产生拉力，从而也就说明了快链条下落时速度快于同高度释放的自由落体运动的速度。

本文研究的快链条是一根由若干与水平面有一定角度的木棍以及两条连接绳构成的链条,如图1所示。

图1 快链条示意图

由于快链条结构的特殊性，快链条在以一定速度撞击桌面后，链条会有一个速度的突增，使得悬空部分链条的连接绳拉紧产生拉力，从而使得悬空部分以大于重力加速度的加速度下落。下面证明这一点。

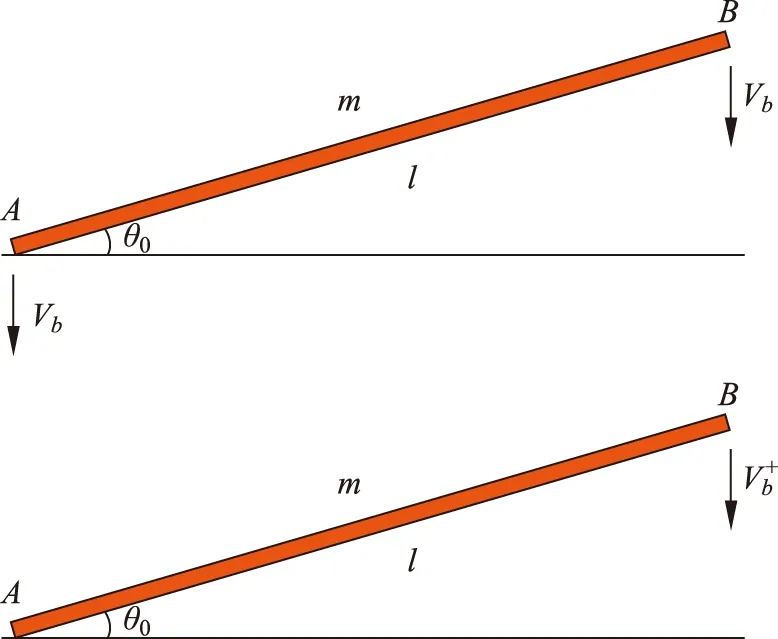
图2 木棍落地前以及落地瞬间的受力分析图

如图2所示，先取快链条最下端的木棍进行分析，假设木棍与地面的碰撞是完全非弹性的，在该木棍与地面碰撞的极短的时间内，左端的速度突变为零，木棍开始做绕左端点A的定轴转动运动。由于在极短的时间内可认为木棍受到外力的冲量矩为零，则由角动量定理[5]可得：

其中，V(x)为链条与地面刚要碰撞之前链条的速度；θ0为木棍与水平面的初始夹角；x为沿杆方向的积分变量；m为单根木棍的质量；l为木棍的长度；ω为链条与地面碰撞后，开始绕A点转动瞬间木棍绕A点转动的角速度。

由于在与地面碰撞之前，木棍上各点的速度均相等，可以都设为Vb，因此角动量守恒的等式化为

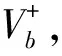
(1)

图3 木棍落地瞬间链条的速度变化

考虑到连接绳不可伸长，则底端木棍右端点速度的竖直分量和悬空部分的速度将很快达到同速，显然该速度将大于悬空部分原来的下落速度，小于底端木棍右端点原来速度的竖直分量，如图3(b)所示。下面推导该速度。

该过程所用的时间极短，则重力产生的冲量矩可以忽略，所以可由角动量守恒定理得到如下式：

其中，n为悬空部分的木棍数量；V+为底端木棍和上方链条达到同速后的共同速度。求解上式得：

(2)

上式表明了在木棍初始倾角满足条件的情况下，每当一根木棍落地悬空部分的链条都会产生一次速度突增，且原速度越大，速度突增的量值也就越大。

为验证上述理论推导得出的结论，本文选用木棍和细绳制作了快链条，并对其下落过程进行了录像，从录像中截取到了如图4所示的快链条下落瞬间的图像。

图4 快链条下落过程中某一时刻的图像

从图4中的标记处可以看出，最底端木棍的一端碰撞地面时，该木棍的另一端与上方未落地链条之间的连接绳处于绷紧的状态。从而验证了上文推导出的因底端木棍速度突增而使得底端木棍与上方未落地链条之间连接绳绷紧的结论。

2 快链条下落过程的定量描述

基于上节的定性分析和速度突增的结论，本节建立描述快链条下落过程的微分方程。

底端链条与地面接触并开始做定轴转动的某时刻的链条如图5所示，设在该时刻未落地的悬空部分有n根木棍，底端木棍此时与水平面的夹角为θ。

图5 快链条受力分析图

由上节分析知T2>0，所以对最下端的木棍由转动定理得：

对悬空部分的链条由牛顿第二定理得：

nmg+T2cosγ=nma

由于连接绳拉直所以沿绳方向上上下两部分的加速度必相等有

acosγ=lβcos(γ-θ)

由上3个式子得加速度为

若每两根链条之间的距离很短，则可认为γ=0，上式化简为

(3)

可以看出要使加速度大于重力加速度g则需满足：

化简得：

该式表明了快链条下落快于自由落体的临界角条件为θ<35.26°，这一结论与第1节的定性分析结果完全一致。

在此基础上，求解任意时刻快链条的位置。考虑到上方木棍数目n是一个离散量，要得到链条下落过程中链条下落距离与时间的关系，首先需要对n的不同取值进行分段求解，且应考虑到每根木棍落地时的速度突增。

设快链条底端木棍碰撞地面的瞬间链条的初速度为Vb，木棍与水平面的初始倾角为θ0，悬空部分的木棍数为n。当底端木棍转过一定角度后，底端木棍与水平面的夹角为θ，底端木棍未落地的一端离地面的竖直距离为X，如图6所示。

图6 快链求解示意图

由几何关系有

将上述两式代入式(3)，则可以得到链条下落过程中底端木棍未落地端的竖直高度X关于时间t的微分方程：

结合速度突变表达式(2)，可以得到确定底端木棍竖直高度X与时间t的微分方程和定解条件为

(4)

该式表明在初始角度满足条件的情况下，当某一节木棍以Vb的初速度落地时，上方的链条瞬间产生速度突增和加速度的突增，并在底端木棍与水平方向的夹角减为零之前，始终按上述微分方程的形式保持着大于重力加速度的加速度，这也间接证明了快链条下落时，链条的连接绳间存在拉力。该现象的本质是底端木棍在撞击地面后动能没有完全损失，而转移了一部分能量到上方未落地的链条。

需要指出的是，上述微分方程和定解条件的求解结果是，快链条的一节木棍落地过程中，快链条底端高度随时间的变化。当求解整个快链条的下落过程时，对木棍撞击地面的过程采用式(4)的微分方程，且由于每节木棍落地时其上方悬空的木棍数目不同，因此每次求解时应改变方程中的n值；对木棍与木棍衔接部分，由于没有木棍落地，绳中没有拉力，应按自由落体求解；同时，应考虑到快链条每段自由落体运动的末速度按速度突增式(2)处理后，才是下一段微分方程的初速度。

综上所述，可不失一般性的将快链条的下落过程按如下过程理解：链条先做自由落体运动，自由落地运动的末速度即为下一节木棍落地前瞬间链条的速度，木棍与地面接触后瞬间链条速度按式(2)规律突增，之后链条按式(4)的微分方程的规律运动，当木棍绕端点转动至倾角为零后，快链条又开始做自由落体运动，如此反复，直到链条落完。

3 数值求解及实验

为验证本文模型的合理性，本节将使用自制的快链条进行实验并通过高速摄影机和Tracker软件对快链条的下落过程进行记录和测量，并将理论计算结果与实验测得结果进行比较。

为初步了解快链条的下落过程，基于本文第1节和第2节所得结论，本文首先针对总木棍数为15根，木棍长度为17.5cm，初始倾角为15°，木棍间间距为1cm的快链条进行数值求解。其中对微分方程的求解借助了Matlab软件的ode45指令。数值求解结果如图8所示。

从图7可以看出，由于快链条加速度始终大于等于重力加速，因此其位移和速度也始终大于或等于自由落体，从位移图像上看，快链条与自由落体的位移差随时间增加逐步增大；从速度图像上看，快链条的速度始终增长的比自由落体快，且可以明显看出由于每根木棍落地时的速度突变；从加速度图像上看，每根木棍落地瞬间链条的加速度瞬间突增，超过重力加速度，且在木棍与水平面夹角逐渐减小的过程中木棍的加速的不断增大，但到夹角完全等于零后，加速度又变回重力加速度，并在下一根木棍落地之前做自由落体运动，加速度保持重力加速度不变。

为验证本文模型的合理性，本文针对具有不同尺寸参数的快链条进行了实验，快链条的结构参数包括木棍间距d，棍长l，初始倾角θ0，因为确定了这3个参数，即可确定快链条的尺寸结构，3个参数的示意图如图8所示。

同时，由于链条速度突增的量值与原速度有较大的关系，因此本实验分别以木棍间距d，的棍长l，初始倾角θ0以及初始速度V0为参数进行实验，通过高速摄影机拍摄快链条的下落过程，将慢速回放的录像导入Tracker软件，再选定快链条顶端的一点进行追踪，并记录该点位置随时间的变化，即可得出快链条下落过程中位置随时间的变化，实验结果如图9到图13所示。其中实验组2到实验组5分别与实验组1形成改变不同参数的对照。

实验组1：木棍数15根，棍长101.63mm，木棍间距8.26mm，初始倾角25.24°，初速度0m/s。

实验组2：木棍数15根，棍长101.63mm，木棍间距16.03mm，初始倾角25.24°，初速度0m/s。

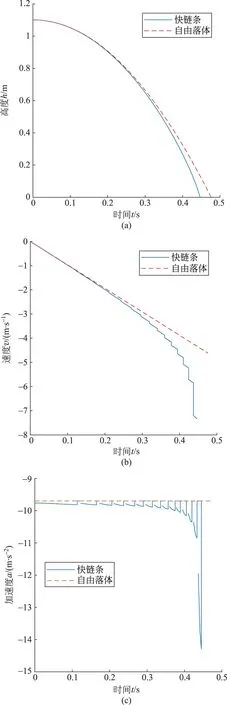
图7 快链条位移，速度，加速度图像(a) 位移图像； (b) 速度图像； (c) 加速度图像

图8 快链条尺寸参数示意图

图9 实验组1的求解结果与实测数据对比图(a) 高度与时间的关系图； (b) 速度与时间的关系图

图10 实验组2的求解结果与实测数据对比图(a) 高度与时间的关系图； (b) 速度与时间的关系图

实验组3：棍数15根，棍长101.63mm，木棍间距8.26mm，初始倾角32.83°，初速度0m/s。

实验组4：棍数15根，棍长201.67mm，木棍间距8.26mm，初始倾角25.24°，初速度0m/s。

实验组5：棍数15根，棍长101.63mm，木棍间距8.26mm，初始倾角25.24°，初速度-0.65m/s。

1) 实验组1与实验组2形成以木棍间距为变量的对照试验

由理论分析可知，在木棍与木棍衔接部分由于没有木棍落地，加速度为重力加速度，不及有木棍落地时的加速度大。所以，棍间的距增大会导致链条在下落过程中有更多的时间处于自由落体，因此在下落了相同距离的情况下，速度小于棍间距较小的链条。实验结果也符合上述的分析。

2) 实验组1与实验组3形成以初始倾角为变量的对照试验

由实验结果可以看出，当初始倾角增大，快链条的位移图像更加接近自由落体，说明了初始倾角的增大会使得快链条下落变慢。对此可做如下解释。

图11 实验组3的求解结果与实测数据对比图(a) 高度与时间的关系图； (b) 速度与时间的关系图

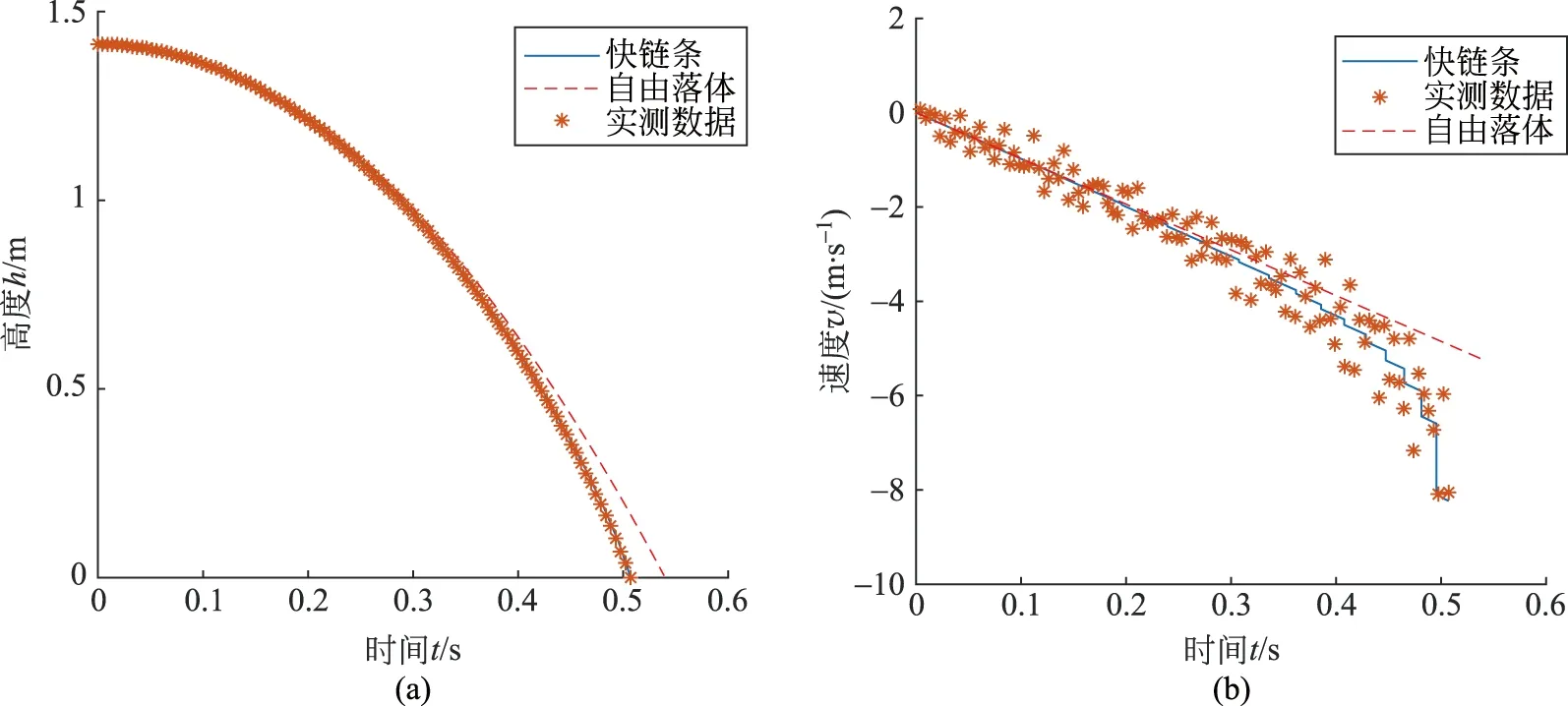
图12 实验组4的求解结果与实测数据对比图(a) 高度与时间的关系图； (b) 速度与时间的关系图

图13 实验组5的求解结果与实测数据对比图(a) 高度与时间的关系图； (b) 速度与时间的关系图

由第2节推导出的加速度公式：

3) 实验组1与实验组4形成以棍长为变量的对照试验

棍长l的增长带来影响，主要体现在两个方面。一方面是，l增大时，会使得每节木棍落地后，木棍未落地一端端点距地面距离lsinθ0增大。另一方面是，由上述加速度的计算公式可以看出，在高度X取值相同的情况下l越大则cos2θ的值越大，从而加速度a越大。

4) 实验组1与实验组5形成以初速度为变量的对照试验

由于在其他参数不变的情况下，每节链条落体时的突增后的速度与原速度成正比，如第1节所推导的公式：

则初速度的增大会导致快链条的速度与自由落体运动速度的差值更快的增大。实验结果也符合上述分析。

4 结论

由上述实验以及理论计算结果，可以明显看出快链条的理论计算曲线相比一般自由落体曲线，可以更好地拟合实测数据点，这很好地说明了在初始角度满足要求的情况下，快链条在下落过程中始终快于自由落体，从而也就间接地说明了快链条下落过程中，链条的连接绳存在拉力。同时实验及理论结果也说明了，快链条的下落过程主要受以下参数的影响，分别为棍长，木棍间距，初始倾角以及初速度。

快链条作为一种结构特殊的链条模型，是对传统链条模型的补充和修正。且由于结构特殊，相比普通链条，快链条与刚性平面碰撞后，快链条机械能的损耗小于普通链条，因此，快链条的链条结构对于如何通过改良物体结构，减少物体在碰撞过程中的动能损耗具有一定启发作用。该实验也可作为中学、大学实验中的运动学趣味实验进行演示，以提高学生的学习兴趣和创新思维。