关于流体力学黏滞及伯努利方程演示实验

路峻岭 顾 晨 秦联华 任乃敬 马泊一

(清华大学物理系,北京 100084)

1 关于流体力学的相关知识[1，2]

1.1 问题的提出——伯努利方程的适用条件以及达朗贝尔佯谬

我们知道，物理学是研究自然界物质的基本运动规律的。为了突出主要矛盾，人们往往设定一些理想物理模型，如质点，刚体，理想气体等等。在这里涉及的理想物理模型是理想流体。理想流体的主要特征指的是不可压缩和没有粘滞性，所谓不可压缩指的是流体中任意一定体积的流体团无论其压强、位置、形状如何变化总是保持体积不变；所谓没有粘滞性指的是流体中一部分流体相对于相邻流体流动时它们之间没有相互作用力(或：固体球或棒在理想流体中运动时不受阻力)。

在设定流体为理想流体，且在作定常流动时，即流体中任一点的流速不随时间变化时，按照欧拉法，可用速度场表示流体，其中的场线就是流线，流线上任一点的切线就表示该点的流速。由流线围成的闭合细管称为流管。由于设定流体为理想流体，没有粘滞性，流动过程中没有能量损耗，机械能守恒。再由质点系的功能原理，把流管中的一段流体体元作为质点系，当它在流管中运动时，外力功等于体元的机械能的变化。由此得到伯努利方程

(1)

其中，ρ为流体的密度；v为流体元的速度；g为重力加速度；h为流体元的高度；p为流体在流体元处的压强；C为常量，它表示流体元中单位体积的机械能。

实验表明，几乎一切流体都具有黏滞性。在物理学史上，先辈们对流体物理图像的理解曾经经历过曲折的过程。在20世纪之前，人们研究流体力学的兴趣和精力都集中在无黏滞假设下一个又一个优美的数学解上。冯·诺埃曼(John von Neumann)意识到这些研究中的问题，他认为这些研究丢掉了流体的一个基本性质——黏滞，故它们是与实际流体不相干的。1869年，开尔文(Thomson.W.Kelvin)给出了一条定理，即在均质理想流体内，沿任一闭合曲线，流体速度的环量不随时间变化，换言之，理想流体中的速度环量守恒。1906年，茹科夫斯基(N.E.Zhukoskii)在研究飞机机翼升力时得到升力公式，公式表明，机翼升力与流体密度、飞机速度和流体绕机翼的速度环量成正比。这就引出了一个矛盾，即按照开尔文定理，理想流体中的速度环量守恒，如果原来没有环量，环量就产生不出来，则理想流体对在其中作匀速运动的固体物体不会施加任何力，既没有阻力也没有横向升力。也就是说，如果把空气看作理想气体，则飞机就飞不起来了。这个结论与实验事实严重不符，称为达朗贝尔佯谬(d’Alembert paradox)。它提醒我们，早年冯·诺埃曼的告诫是有道理的。1880年前后，雷诺(O.Reynolds)做了大量实验，研究流体运动的规律。他发现，影响流体运动的不仅仅有黏滞系数η，而且更重要的是被后世(索末菲起始)称为雷诺数的无量纲组合参量Re。

(2)

其中，ρ为流体密度，v为流体与运动物体的相对速度，d为圆管直径(或运动物体的线度)，η为流体的黏滞系数。当雷诺数Re很小时，流体的运动表现为层流和稳流，随雷诺数Re的由小变大，流体的运动表现为由层流渐渐变为湍流。如果我们把注意力集中到运动流体中的某一体元上，它的运动决定于周围流体对它的作用，同时它也有力的作用施加于周围的流体上。在考虑到黏滞时，运动中的流体元与其相邻流体有切向相互作用。每一个流体元都是在这些相互作用下运动着。如果这些相互作用未能改变流体宏观速度场的形态，则流体流动表现为层流；如果这些相互作用改变了流体宏观速度场的形态，流速场出现了许多局域突变，则流体流动表示为出现了湍流。

实际上，研究对象某一个参量的连续变化，引起其运动方式出现突变的例子比比皆是。例如我校六教展厅中的小孔泄漏实验、水中落沙实验和圆柱状刚体平面平行运动实验都是其典型实例。

小孔泄漏实验中，在一个玻璃杯的中部设置一个中间有一小圆孔的水平隔板，杯的上下部分别注入相互可以完全溶混的溶液(例如上部注入浓盐水或浓糖水下部注入纯净水)，在物理势和化学势的共同作用下，两种液体将通过小孔进行溶混。如果小孔的直径足够小，则小孔只允许某一种液体以层流的方式通过，溶混过程表现为两种液体轮流通过的振荡过程；如果小孔的直径很大，则小孔可让两种液体以湍流的方式迅速溶混，没有振荡过程出现。如果令小孔直径由小到大连续变化，则溶混过程表现为由层流振荡变为湍流溶混的半随机过程。

水中落沙实验中，先在一段玻璃管中放入一把细沙，再注满纯水，并密封之。实验时，实验者手持此玻璃管竖直放置，水中细沙在重力的作用下慢慢地沉到底部。然后，实验者突然转动玻璃管到一定角度并停止住，观察玻璃管中细沙的下落过程。若实验者转动180度即停止住，则细沙将从玻璃管的顶端(上端)慢慢下落，每一个沙粒都独立地在水中下落；若实验者转动135度后即停止住，则细沙将从倾斜着的玻璃管的上端迅速下落，众细沙将团结为一个整体滚动下落，且后者的下落比前者快得多。如果实验者连续改变转动停止住的角度，则水中细沙下落过程将从颗颗细沙单独下落方式逐渐变为联合为一体滚动下落方式。

图1 单参量连续变化引起运动方式突变实例

圆柱状刚体平面平行运动实验中，用细丝线绕在线轴状刚体的细轴上，单调改变拉线倾角会引起刚体的不同形式的运动。三个实验都是改变一个因素而使物理过程发生突变的实例。

现在看来，把黏滞系数为零作为理想流体的基本条件是有很大局限性的，即理想流体作为物理学研究对象的适用范围是很小的。现在的问题是，如果考虑了流体的粘滞性，如何演示流体的粘滞性和流体力学中的伯努利方程呢？

1.2 具有黏滞性的流体的运动方程

设粘滞性流体在圆形管道内作定常流动(层流或稳流)，设想在流体中隔离出一个圆筒状薄流体层，如图2所示，其几何尺寸亦见图2所示。

图2 柱坐标中圆筒状流体薄层的受力分析

按照牛顿(内摩擦)黏滞定律，其内外侧面(圆柱侧面)受到的粘滞力(水的黏滞系数与温度有关，0℃时为1.79×10-3Pa·s,20℃时为1.01×10-3Pa·s,50℃时为0.55×10-3Pa·s,100℃时为0.28×10-3Pa·s)(z方向)为

(3)

圆筒状薄流层受到的粘滞力合力(沿流线方向z方向)

在定常流动情况下，此力与圆筒状薄流层上下游的压强差提供的力(z方向)相平衡，

(4)

(5)

体积流量

(6)

平均流速

(7)

在流体内部，半径为r=αR(0≤α≤1)的小圆形流管中的平均速度

(8)

当α→0时，

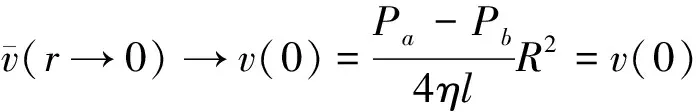
(9)

当α→1时

(10)

从内摩擦引起机械能损耗出发，由(3)式可知，即使是水平管道，要保持在一定长度的管道上有一定的流速也一定要有压强差，这是与理想流体完全不同的。李复老师根据功能原理，研究黏滞流体稳流(层流)情况下的伯努利方程，得出考虑了内摩擦的伯努利方程为

(11)

式中w12(>0)为流体元从位置1沿流线流动到位置2时，单位体积的流体克服黏滞阻力所做的元功。若通过水平细直玻璃管道演示黏滞现象，则位置1和位置2对应的流速、高度均相同，则由(11)式可得

p1=p2+w12→p1-p2=w12>0

(12)

即可知：沿着流动方向(水平方向)流体的压强是逐渐降低的，即可通过粘滞性流体沿水平方向流动时，压强的逐渐降低来演示黏滞现象。

2 用水作为黏滞流体来演示黏滞现象

2.1 黏滞现象实验装置介绍

把水作为黏滞流体来演示黏滞现象的实验装置的示意图如图3所示。一个大圆筒形容器，横截面积为S0，底部连接一个水平圆形细管，长度为L，横截面积为S1，且S0≫S1。在水平圆形细管上等间距地均布4根竖直(垂直于水平面)的细管，作为压强指示器。

图3 用水作为黏滞流体来演示黏滞现象的实验装置

实验时，先堵住水平细管的出口，往大圆筒形容器中注入清水，然后令水平细管的开口开启，让水自行流出，观察各个竖直细管(压强指示管)中水柱高度的分布。实验发现，水沿水平细管往下游流动时各个竖直细管中(压强指示管)的水柱高度依次降低，各水柱的上端都在同一条直线上。由于大圆筒形容器横截面积比水平横细管的大得多，大圆筒形容器中的水面高度下降得很慢，所以可以很容易地看到相对稳定的实验图像。

2.2 黏滞现象演示实验的定量分析[2]

(13)

在水平细管中应用泊肃叶流量公式(6)和平均流速公式(7)，则得

(14)

再，由于流体不可压缩，水平细管流出的流体(体积)等于大圆筒形容器流体的减少，则

(16)

(14)与(15)式等价，解(13)(14)联立方程组(H0为设定值)，把(14)式代入(13)得

(17)

解此关于H1的一元二次方程组，可得其大于零的解(H1大于零才有意义)

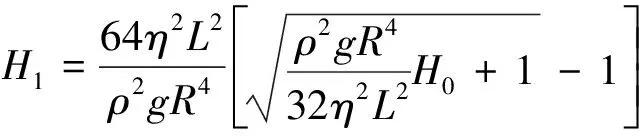
(18)

将(18)式代入(14)式可得

(19)

2.3 大圆筒形容器中水面高度H0随时间t的变化

把(16)代入(19)式，可得关于水面高度H0的微分方程

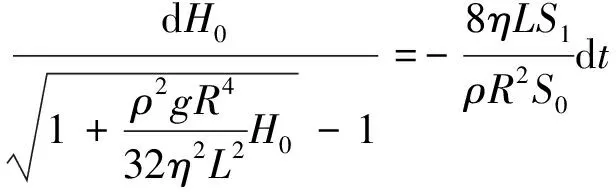
(20)

设初始条件为

H0(0)=H00

(21)

为了求解此微分方程，令

则微分方程(20)式化为

两边积分，可得

(22)

其中，C为积分常数，由初始条件确定。 为了使结果易读且明显，可记H0=x，当t=0时，x(0)=H0(0)=H00，由此得

则把它代入(22)式得最后结果

(23)

这就是流体黏滞实验中，流水时间t随大圆筒形容器中水面高度H0的变化关系式。

3 用水作为黏滞流体来演示伯努利方程实验

3.1 实验思路

在大学物理教学中，为了演示伯努利方程，常常选用一根直玻璃圆管作流管(见图4)，水平放置以消除高度的影响，在玻璃圆管的不同位置设置若干个膨大区(制作时设置若干气泡区)，以使其内径不同。流体在其中流动时，内径小的流管处的横截面积小，内径大的流管处的横截面积大。在层流前提下，沿流线的各个横截面上的流量相同，内径小的地方流速快，内径大的地方流速慢。按照伯努利方程，内径小的地方流速快则压强应该小，内径大的地方流速慢则压强应该大。若能够演示出这些压强的变化，即表示演示出了伯努利方程。

图4 用水作为黏滞流体来演示伯努利方程的实验装置

实际实验现象亦如图4所示。但伯努利方程是建立在理想流体的基础上的，而通常人们所见到的流体都是黏滞流体，考虑黏滞后如何演示伯努利方程？或者说，考虑黏滞后又如何利用伯努利方程的概念来解释图4所示的实验现象呢？

3.2 粘滞流体在水平圆形管道中流动时其横截面上的压强分布

本实验的标示参量是流管中一点的压强，如图6所示，在水平直玻璃圆管的正上方侧面上设置竖直侧枝管，以侧枝管中水柱的高度表示流管中流体的压强。现在的问题是：每一根侧枝管中水柱的高度表示流管中哪一点的压强？在粗细流管侧面设置的两个不同侧枝管中水柱的高度所表示的压强有没有可比性？

以圆形流管的水平中心线(向右为正)为z轴，以竖直线(向上为正)为y轴建立直角坐标系，同时以流管的水平中心线(向右为正)为z轴，建立柱坐标系。

设在某时刻，在流体中分割出一个立方体形微元，考虑到它的各个面上受到的正压力、黏滞力以及微元所受的体积力(与体积有关的力)，列出牛顿第二定律方程。考虑到均质、不可压缩，得到如下纳维-斯托克斯方程[2-4]

(24)

式中，ρ为流体的密度；为流体元的速度；η为流体的黏滞系数；p为流体元处的压强；f为单位体积的流体所受到的体积力(与体积有关的力)。具体到我们现在用水作为流体，其体积力就是重力，f的大小等于重力加速度，方向是竖直向下。式(24)实质上是牛顿第二定律在流体力学中的具体形式。

当水在水平流管中作稳定流动(即层流)时，若忽略了流管横截面上各点的重力引起的压强差(细流管近似)时，流管中的流速如下式所示[1]，

它只有沿流线方向z的分量，且不随时间变化。因此，流体元的加速度为零，(24)式化为如下(25)式。

p=η2+ρf

(25)

具体到本实验，(25)式的右边两项分别只有z方向和-y方向的分量，故它的分量形式为

图5 以玻璃圆管中心线为中心线的细流管

(26)

在这儿，由(26)式的前两式可见，流管中任一横截面上的压强分布，如同一桶静水中的一个竖直平面内的压强分布一样，静水内部的压强仅与其深度(参量为y)有关。水深处(y值较小)的压强大，水浅处(y值较大)的压强小。

(27)

这就说明，流管中任一横截面上的一点处，压强沿流线方向的压强梯度，就是维持粘滞流体稳定流动所需要的压强逐渐降低的变化率。

总之，若在水平直玻璃圆管中有水在作稳定流动(层流)时，管中处处流线都平行于水平直玻璃圆管的中心线；在垂直于流线的横截面上，平面内任一点的压强，均如同静水中一样，仅与其深度相关，待测点的位置越低深度越深压强越大；压强在沿流线方向上是逐渐降低的，压强沿流线方向的压强梯度，就是维持粘滞流体稳定流动所需要的压强逐渐降低的变化率。由于图4中粗细两段流管的中心线是同一条直线，直线上的点都在同一水平上，因此两个侧枝管中的水柱高度差就表示在粗细部两段流管中心线上两侧枝管处的压强差。

3.3 用水作为黏滞流体进行伯努利方程演示实验的物理图像

由于图4所示复合玻璃圆管的中心线为一条水平直线，直线上各点的压强具有可比性，故我们研究以此水平线为中心线的细流管中流体运动的规律，如图5所示。

在细流管中，於a1位置和a2位置分别作流管的横截面，细流管的截面积分别为SB和SA。设经历一微小时间间隔Δt，SB从a1移动到b1，SA从a2移动到b2，由于流体不可压缩，则左端流入的体积等于右端流出的体积，即SBΔB=SAΔA=ΔV。对a1到a2这段流体运用机械能守恒定律。由于其中从b1到a2段的一段里虽然流体更换了，但由于流动是稳流(层流)，是定常的，其运动状态没有改变。所以只需考虑两个流体元段SBΔB、SAΔA运动状态和机械能的变化。若不考虑黏滞，则机械能守恒，据此可以得到伯努利方程。若考虑黏滞，则必须考虑机械能损耗，黏滞阻力做负功，这一负功为流管上下游压强差所做正功所抵消，以使流体保持稳流状态。

如图5所示，在以玻璃圆管中心线为中心线的细流管中，在粗部，由黏滞阻力做负功与压强差所作的正功相等，可得

(28)

所以，fB=(PB-PB′)SB，即：黏滞阻力等于两端压强差与横截面积的乘积，黏滞阻力功等于两端压强差与体积流量的乘积。

在中心细流管的细部，按照类似思路和步骤亦可得到类似的结果

(PA′SA-PASA)ΔA=(PA′-PA)SAΔA=(PA′-PA)ΔV=fAΔA和fA=(PA′-PA)SA，即：黏滞阻力等于两端压强差与横截面积的乘积，黏滞阻力功等于两端压强差与体积流量的乘积。注意到这一结果与截面直径无关，可以想见，上述结果也适用于过度段，或者包含过度段的流管。由此可知，由机械能变化规律得到的伯努利方程在考虑到黏滞后必须修改为[2]

式中w12(>0)为流体从位置1沿流线流动到位置2时，单位体积的流体克服黏滞阻力所做的功。若通过水平粗细直复合玻璃管道演示伯努利原理，则位置a1和位置a2对应的流量、高度均相同，则由上式可得

(29)

即

(30)

(30)式表示：在中心细流管中，位置a1和位置a2处的压强差与细流管横截面积及黏滞损耗之间的关系。其中QV是水流过中心细流管中位置a1和位置a2处的体积流量。我们知道本实验中粗细流管处的压强差是观察参量，它与位置a1和位置a2处细流管横截面积的关系就是我们要演示的伯努利定理。若w12=0，(30)式表示的就是理想流体的情况；若w12>0，(30)式表示的就是黏滞流体的情况。欲把水当作近似理想流体来做实验，则必须使黏滞损耗w12相对于(30)式中右边其它项要小得多才行，即

(31)

定性分析，欲使上式成立，须使：①玻璃管粗细部的直径的差别大一些更好；②若粗细部的直径比例一定时，则直径都更大一些以使相应的流量大一些更好；③欲使黏滞损耗小一些，表示流体压强的两个侧枝玻璃管之间的距离(含过度段)尽量小一些更好。

总之，本实验演示的是：在具有粗细两种直径的复合圆直玻璃管中，在其中心线附近的细流管的流速与压强的关系，即伯努利原理。玻璃管细的地方其中心细流管也细，流速大，压强低；玻璃管粗的地方其中心细流管也粗，流速小，压强高；压强的差别通过侧枝管中的水柱高低表示出来。

需要指出的是，由于黏滞的存在，流体的压强总会沿流线的方向逐渐降低。为了减少它的影响，建议本实验装置选取流体由玻璃管细部流向粗部方向，在粗部，伯努利原理要求它的压强较高，若压强真地较高，说明伯努利原理是正确的。因为黏滞总会使下游的压强有所降低，在压强有所降低的情况下，下游的压强仍然较高，说明下游粗部的压强确实较高，说明伯努利原理是正确的。否则，若选取流体由玻璃管粗部流向细部方向，在细部，伯努利原理要求它的压强较低，若压强真地较低，则不能确切地说明这是不是黏滞在起主要作用，因此不能显然地说明伯努利原理是正确的。

3.4 伯努利方程演示实验的改进方案

由于黏滞流体在玻璃直圆管中定常流动时，即便是把中心线附近的细流管作为研究对象，其压强也总会沿流线方向逐渐降低，为了消除黏滞的影响，我们选择如图6所示改进方案。把粗管部或细管部分为前后两部分，

中间为比较部。流

图6 伯努利方程演示实验的改进方案

线由前部流到比较部，由于黏滞的影响其压强会逐渐降低，再由比较部流到后部时，其压强会进一步降低。若玻璃管的结构对称，则两段过程的压强降低一定相同。所以，如果以前后部圆管处的压强的平均值(连接前后部压强液柱顶点的直线交比较部压强指示管对应的压强值)作为前后部圆管在比较部圆管处的压强值，就消除了黏滞对前后部圆管压强的影响。再与比较部圆管处的压强相比较，就等效为消除了黏滞以后前后部圆管与比较部圆管的压强的差值。

图6中甲可用于演示气体流体的伯努利方程，压强的显示通过一根与三个压强显示管相连接的连通器(注入显示液红墨水)来实现，注意其中液柱越高表示流管中压强越低；图5中乙可用于演示液体流体的伯努利方程，液体流体在相应压强显示管中的高度，即表示流体在该处的压强。