基于故障概率的配电设备排查路径规划

马天佚，朱建明，杨 霖，张 驰

(1.国网北京城区供电公司，北京 西城 100035 ；2.中国科学院大学工程科学学院，北京 石景山 100049)

配电系统结构复杂，设备分散，对停电发生时故障设备的准确定位造成了一定的困难，极大影响了应急抢修、应急电源接入等配电网应急管理手段与效率[1-2]。现阶段配电自动化技术的应用尚未成熟，多数情况下仅能划定故障设备所处区域，难以准确定位，仍需抢修人员对故障区域内的设备进行排查以确定故障点。因此，排查路径的优劣直接影响配电系统应急抢修工作效率。目前关于电力系统及相关领域应急路径规划的研究主要集中在目标位置明确时的最短路径规上，国内外学者通过很多优化模型和算法对此类问题进行了深入研究。但是，对于故障点不确定情况下的故障排查路径规划鲜有报道，而这是现阶段配电系统乃至整个电力系统需要解决的主要问题之一。

本文针对停电事件发生时故障点仅被划定在某一区域内的排查路径规划进行系统研究，同时考虑到配电设备故障概率的差异性，对基于设备故障概率的排查路径进行深入探讨，类比旅行商问题(TSP)建立排查路径规划模型并应用遗传算法对其进行求解，确保在停电事件发生时，合理规划排查路径，及时定位故障设备，提高配电系统应急能力。

1 排查路径规划模型的建立

传统的应急抢修路径规划研究主要致力于以“总时间最短”或“总路径最短”为单一目标的路径最短化问题。文献[3]以停电用户满意度衡量的总时间最短为目标，考虑到路径行驶时间的区间性，运用二分法构建应急电源路径优化模型；文献[4-10]以“总路径最短”为目标，分别依托迪杰斯特拉算法(Dijkstra)、小波变换法、弗洛伊德算法(Floyd)、粒子群算法、Critic、拉格朗日数乘法等不同形式的最短路径算法，对应急抢修路径进行规划选择。

然而，实际运行中，配电系统设备种类繁多，设备类型、运行年限、制造工艺、所处环境等因素各不相同，因此配电设备的故障概率存在较大差异[11-16]。仅以“总时间最短”或“总路径最短”为目标无法将不同设备的故障概率差异纳入总体规划，以确保大故障概率设备的排查优先性。当考虑设备故障概率的差异性时，故障点被划定在限定区域内的排查路径规划问题可以看作一个多目标组合优化问题，其规划目标有两个：一是排查工作的及时性，即抢修人员从接到故障信息，获知故障限定区域开始， 以最快的速度找到限定区域内故障设备的准确位置。该目标可以转化为抢修人员从初始位置开始，遍历故障限定区域内的所有配电设备的所需时间的最小化，即传统研究中以“总时间最短”或“总路径最短”为目标的路径规划问题；二是排查工作的准确性，即抢修人员在考虑时间或路径最短化的同时，以最大的概率优先排查出限定区域内故障设备的准确位置。该目标可以转化为抢修人员在保证时间最短化的同时，优先对限定区域内故障概率较大的设备进行排查。

综上所述，该问题可以描述为：在已知抢修人员初始位置、故障限定区域、限定区域内设备数量、各设备实际位置、故障概率以及通过各行驶路径所需的时间的前提下，抢修人员从初始位置出发，逐一排查限定区域内的所有配电设备，如何规划排查路径，以兼顾路径时间的最小化和大故障概率设备的优先性。该路径规划模型的建立分两步进行，第一步是在不考虑设备故障概率的情况下，以排查“总时间最短”为目标，规划排查路径；第二步是在此基础上，综合考虑设备故障概率，建立“总时间最短”和“大故障概率设备优先级最高”为双目标，优化排查路径规划。

1.1 不考虑设备故障概率时的排查路径

首先仅以排查工作的及时性作为目标，认为限定区域内配电设备的故障概率相同。此时的排查路径规划问题可以看作典型的旅行商问题(TSP)，可将故障限定区域抽象为无向赋权图，抢修人员的初始位置和配电设备的位置即为图的顶点，各顶点间的行驶时间即为图的边权，选择一条从抢修人员初始位置开始遍历限定范围内所有配电设备的路径，使得经过该路径所需的时间最短。即针对限定区域内的配电设备集合J={1，2，…，j}，求解最佳排查路径π(J)={V1，V2，…，Vj}，使得：

(1)

其中，Yj为目标函数；j为故障限定区域内配电设备数；S为抢修人员初始位置；t(S，V1)为抢修人员初始位置S到第一个排查的设备V1所需的时间；t(Vi，Vi+1)为抢修人员从第i个排查的设备Vi到第i+1个排查的设备Vi+1的所需的时间。

1.2 考虑设备故障概率时的排查路径

在式(1)所建立的路径规划模型的基础上，计入配电设备的故障概率，即针对限定区域内的配电设备集合N={1，2，…，n}，求解最佳排查路径π(N)={V1，V2，…，Vn}，以兼顾排查时间的最小化以及大故障概率设备的优先性，使得：

(2)

其中，Z为目标函数；n为故障限定区域内配电设备数；PVj为设备Vj的故障概率。该模型的目标时抢修人员从初始位置出发，遍历限定区域内的所有设备，且到达某设备前所经历的时间与该设备故障概率的乘积之和最小化。

2 模型求解

上节所建立的两个排查路径规划模型均与旅行商问题问题(TSP)类似，是NP完全问题(NP-complete)，其可行解为无向赋权图中所有顶点的全排列，复杂度随着图中顶点数目的增加呈指数倍增长。因此，当故障限定区域内设备数量较大时，无法使用精确算法进行求解其最优解，只能采用近似算法求解求解较优解。本文拟采用启发式算法中的遗传算法对该问题进行求解。

遗传算法(genetic algorithm)是一种通过模拟生物进化过程和遗传机理搜索近似最优解的算法，可用于解决复杂的非线性优化问题，常被用于规划计算类研究[17-19]。遗传算法首先随机生成初始种群作为所求问题的初始解，并设定最大遗传代数。种群由通过基因编码的个体染色体组成。然后，根据所求问题的目标函数规定适应度函数，并通过选择、交叉、变异、进化逆转等操作，按照优胜劣汰、适者生存的原理，逐代演化产生适应度更高的种群。当达到设定的最大遗传代数后，选取其中适应度最大的个体染色体，并将其解码，作为问题的最优近似解。具体流程如图1所示。

(1)问题参数：包括抢修人员初始位置、限定区域内设备数量、位置和故障概率、通过各行驶路径所需的时间等实际参数以及初始种群中个体染色体数目m、选择概率Ps、交叉概率Pc、变异概率Pm、最大遗传代数maxgen等设定值；

(2)编码：当限定区域内配电设备数量为n时，首先对设备分别编号，形成设备集N={1，2，…，n}，然后将遗传算法中个体染色体分为n段基因，每一段基因即为一个设备编号，如个体染色体|1|2|…|i|…|n|就表示排查路径顺序为1→2→…→i→…→n；

(3)生成初始种群：根据第1步中设定的初始种群的个体染色体数目m以及限定区域内配电设备数量n，随机生成一个大小为m×n的初始种群，作为该问题的初始解集；

(4)适应度函数：根据实际问题的目标函数建立适应度函数，对种群中的个体染色体计算适应度。由于遗传算法默认为求取问题的最大值，而本文的排查路径规划问题需要求解目标函数的最小值，因此考虑将目标函数的倒数作为遗传算法的适应度函数，即对于种群中的个体染色体|k1|k2|…|ki|…|kn|，根据是否考虑设备故障概率，分别建立如式(3)和式(4)的适应度函数：

不考虑设备故障概率时：

(3)

考虑设备故障概率时：

(4)

其中，t(S，k1)为抢修人员从初始位置S到第一个排查的设备k1所需的时间，t(ki，ki+1)为抢修人员从第i个排查的设备ki到第i+1个排查的设备ki+1所需的时间。

(5)选择：根据设定的选择概率Ps，从旧种群中选择适应度函数较大的个体染色体进入新种群；

(6)交叉：在选择操作后，对种群中的个体两两分组，根据设定的交叉概率Pc，随机在每组两个个体的染色体中分别选择两个相对应的位置，并将这两个位置中间的基因进行互换(产生基因重复时需进行修正)；

(7)变异：在选择、交叉操作后，根据设定的变异概率Pm，在种群的个体染色体上选择两个位置，将两个位置的基因进行互换；

(8)进化逆转：在选择、交叉、变异操作后，任意在种群中个体染色体上选择两个位置，将两个位置中间的基因逆向排列，然后对逆转后个体的适应度函数进行计算，当逆转后个体适应度函数增大时，以新个体取代旧个体，否则舍弃新个体保留旧个体。

(9)循环条件：判断循环次数是否达到设定的最大遗传代数maxgen，当达到时，循环结束，否则，继续进行循环操作；

(10)解码：针对遗传算法最终得到的适应度最大的个体染色体，将其解码为基因段，以得到实际问题的近似最优解。

3 算例分析

以某配电系统为实例，验证提出的排查路径规划模型和遗传算法的可行性和有效性。该限定区域交通网络图如图2所示。假定抢修人员的初始位置为S，限定区域内的配电设备共12台，分别编号为{1，2，…，12}，则网络图中共13个顶点，顶点坐标和设备故障概率见表1。抢修人员从初始位置开始可以选择多条路径进行排查，根据实时路况信息可以得到所需的路径时间，单位为min，标注在网络图中。

表1 限定区域内设备坐标及故障概率Tab.1 Coordinate positions and failure probability of the equipment in defined areas

在不考虑设备故障概率和考虑设备故障概率两种情况下，分别根据式(3)和式(4)建立路径规划模型，并应用遗传算法进行求解。

首先确定问题参数，故障区域已限定于图2所示范围内，其中抢修人员初始位置及12台配电设备的位置坐标、故障概率以及抢修人员初始位置数据可由表1得出，通过各行驶路径所需的时间已由图2标注。经过笔者多次试验分析及计算结果比对，在不影响计算精度及收敛速度的情况下，设定初始种群中个体染色体数目m为1 000，选择概率Ps、交叉概率Pc均为0.9，变异概率Pm为0.05，最大遗传代数maxgen为100。

其次对图2限定区域内的配电设备进行编号，形成设备集N={1，2，…，12}，即每个个体染色体由12段基因组成，每一段基因表示的数字即为一个设备编号，编号次序即为设备排查顺序。由此可形成一个含1000个个体染色体的初始种群。

然后，在不考虑设备故障概率和考虑设备故障概率时，分别根据式(3)和式(4)建立最优路径规划的适应度函数。运用遗传算法，依次通过选择、交叉、变异、进化逆转循环过程，选出适应度最高的个体染色体，即为最优路径规划的近似解。

从初始种群出发，在选择环节中，根据选择概率0.9，从1 000个初始染色体中选择900个适应度较大的个体染色体进入新种群；之后进入交叉环节，对选出的900个个体染色体两两分组形成450对染色体组，以0.9的交叉概率决定每对染色体组是否执行交叉，如果执行交叉，则在每对的两个个体染色体中随机选择一个位置，将两个染色体相应位置的基因进行互换；然后进入变异环节，以0.05的变异概率决定每个个体染色体是否执行变异，如果执行变异，则在该染色体上随机选取两个位置，互换这两个位置的基因；然后进入进化逆转环节，在900个个体染色体上选择两个位置，将两个位置中间的基因逆向排列，比较逆转前后的适应度，根据适应度大小决定是否进行逆转。此时即完成1次循环。当循环次数未达到最大遗传代数100时，以此时形成的新种群再次进入选择、交叉、变异、进化逆转环节，直到达到设定的最大遗传代数。

最后，针对100次循环后得到的适应度最大的个体染色体，根据其中12个基因的顺序，得出近似的最优规划路径。

为比较该模型及算法的实用性及有效性，本文对无路径规划方案、不考虑设备故障概率的排查路径方案和考虑设备故障概率的排查路径方案三者进行对比。

(1)无路径规划方案时，抢修人员随机选择排查路径(假定其按照设备编号顺序排查)，此时的排查路径为S→1→3→2→4→5→6→8→10→7→9→12→11，总路径时间为69 min，计及设备故障概率的路径时间为22.439 4 min。

(2)不考虑设备故障概率时，以式(3)为适应度函数建立路径规划模型，并运用遗传算法进行求解。根据问题的参数设定，种群中个体染色体数目m为1 000，最大遗传代数maxgen为200，选择概率Ps为0.9，交叉概率Pc为0.9，变异概率Pm为0.05，将适应度函数及设定参数带入算法中，计算得出的排查路径为S→1→6→8→5→3→2→4→7→9→10→11→12，总路径时间为50 min，计及设备故障概率的路径时间为17.069 3 min。

(3)考虑设备故障概率时，以式(4)为适应度函数建立路径规划模型，同样运用遗传算法进行求解，问题参数设定值同上。此时计算得出的排查路径为S→2→4→7→9→12→11→10→8→5→3→1→6，总路径时间为56 min，计及设备故障概率的路径时间为13.108 3 min。

对三种情况下排查路径规划方案的优劣进行对比，如表2所示。

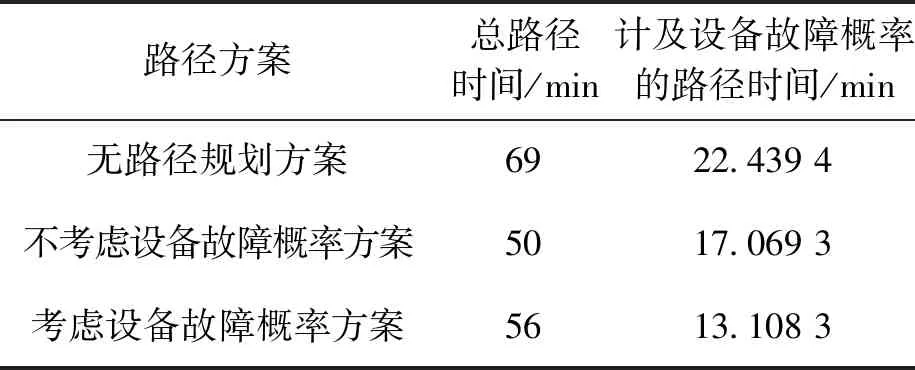
表2 排查路径方案对比Tab.2 Comparison oftroubleshooting path schemes

可以看出，对排查路径进行合理规划后，总路径时间和计及设备故障概率的路径时间均得到明显改善。

(1)与无路径规划方案相比，不论是否考虑设备故障概率，路径规划后的总路径时间和计及设备故障概率的路径时间均大幅降低。在“不考虑设备故障概率”的方案中，总路径时间减少27.54%，计及设备故障概率的路径时间减少23.93%；在“考虑设备故障概率”的方案中，总路径时间减少18.84%，计及设备故障概率的路径时间减少41.58%。可以看出，相较于无规划的设备排查，合理的抢修路径规划能够大幅改善排查工作的及时性与准确性。

(2)对比分析“不考虑设备故障概率”与“考虑设备故障概率”两种情况下的路径规划方案，在“考虑设备故障概率”的方案中，总路径时间较“不考虑设备故障概率”方案增加12%，计及设备故障概率的路径时间减少23.21%。结果表明考虑设备故障概率时的排查路径及时性稍弱，但排查准确性明显增强。两种路径规划方案的区别具体体现在对设备4、设备7、设备9和设备12的排查顺序上，由于设备4、设备9和设备12的故障概率(分别为0.053 4、0.067 3、0.074 5和0.168 5)较其他设备明显增大(平均故障概率为0.0134 6)，因此，考虑设备故障概率时的路径优先考虑对设备4、设备7、设备9和设备12的排查，更可能优先找到故障点，体现了其兼顾时间最小化和大概率故障设备优先性的整体思路。

4 结论

本文对配电系统设备故障时，故障点被限定在某一区域内的排查路径规划问题进行了分析研究。首先，为兼顾路径时间的最小化和大故障概率设备的优先性，提出以计及设备故障概率的路径时间作为规划目标，综合考虑“总时间最短”和“大故障概率设备优先级最高”，进行排查路径规划。其次，针对该多目标组合优化问题，分两步进行模型建立，先不考虑设备故障概率，类比于旅行商问题(TSP)建立路径规划模型；在此基础上，考虑设备故障概率，在保证路径时间最短的前提下，确保大故障概率设备的排查有限性，对模型进行改进，得出基于配电设备故障概率的排查路径规划模型。然后，运用遗传算法对该模型进行求解并对求解过程进行详细说明。最后，以算例对所提出的模型及算法的可行性和有效性进行了分析论证。结果表明本文所提出的排查路径规划模型能够大幅提升排查工作的及时性和准确性，对于提升配电系统应急抢修能力具有重要的参考价值。