高中物理教学中的方程思想

刘昕浩

(广东省惠州星火教育惠州分公司 516000)

物理不仅仅是一门理论学科同样也是一门语言学科，就像学习英语是为了和外国人交流，学习C语言是为了对芯片下达指令一样，受到麦克斯韦方程组的启发，我认为物理是一门描述自然现象的语言，越是高级的方程组能够描述的自然现象就越多，我将这种思想融入了我的高中物理教学中，把解决物理问题的过程简单地分为两步，通过方程描述题目中的现象，然后求解得到题目中的未知量.从而帮助学生找到解题思路，并使学生对物理定律有更高一级的理解.

一、方程思想在匀变速直线运动中的应用

根据匀变速直线运动的常用公式，我们可以将其看做四个基本方程，由这四个方程可以描述出所有的匀变速直线运动.

方程包含的物理量vt=v0+atv0;vt;a;ts=v0t+12at2v0;s;a;t2as=v2t-v20v0;vt;a;sst=v0+vt2v0;vt;s;t

如果一个方程要有唯一解，则方程中只能包含一个未知量，那就说明对于一个单过程的匀变速直线运动问题的话，题目必然会给出v0;vt;a;t;s五个物理量中的三个.即使面对多过程的匀变速直线运动问题，也只需对两个阶段分别列出方程联立方程组求解.

题目选自2018年惠州高三第一次调研考试第23题：一平直的传送带以速率v=2m/s匀速运行，在A处把物体轻轻地放到传送带上，经过时间t=6s，物体到达B处．A、B相距L=10m．求：

(1)物体在传送带上匀加速运动的时间是多少?

(2)如果提高传送带的运行速率，物体能较快地传送到B处．要让物体以最短的时间从A处传送到B处，传送带的运行速率至少应为多大?

(3)若使传送带的运行速率为10m/s，则物体从A传送到B的时间又是多少?

根据题干的条件我们知道了物理在传送带上的运动可分为两个阶段，第一阶段匀加速，第二阶段匀速，题干中告诉我们的信息有物体在第一阶段的初速度与末速度，以及两个阶段总的位移与时间，于是我们可以列出方程描述题干中的情景.

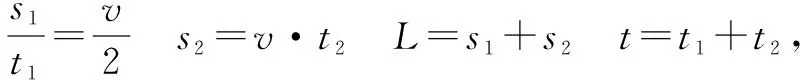
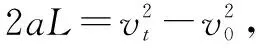
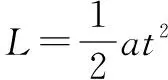
通过方程思想，在读完题目的那一刻就可以很快的找到解题思路，解决了学生找不到思路和记住了公式却不会用的问题.

二、从方程思想看带电粒子在磁场中的运动

带电粒子在磁场中的运动问题是高二学生的难点，其中学生最大的困难在于不会用几何方法计算粒子运动的半径.这里我们可以通过方程思想来简化这个问题.

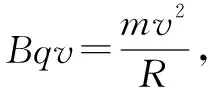
1.弦长、半径、速度与弦的夹角(或圆心角)

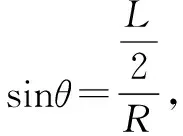
图1

2.在平行边界中

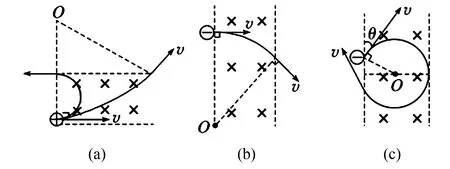
图2

在图2a中，如果边界宽度为d，边界长度为L，运动轨迹半径为R，从右侧射出的粒子的运动轨迹半径可以由勾股定理可以得到L2+(R-d)2=R2，从左侧射出的粒子运动轨迹半径刚好等于边界宽度的一半R=d/2.

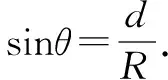
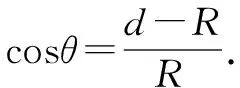
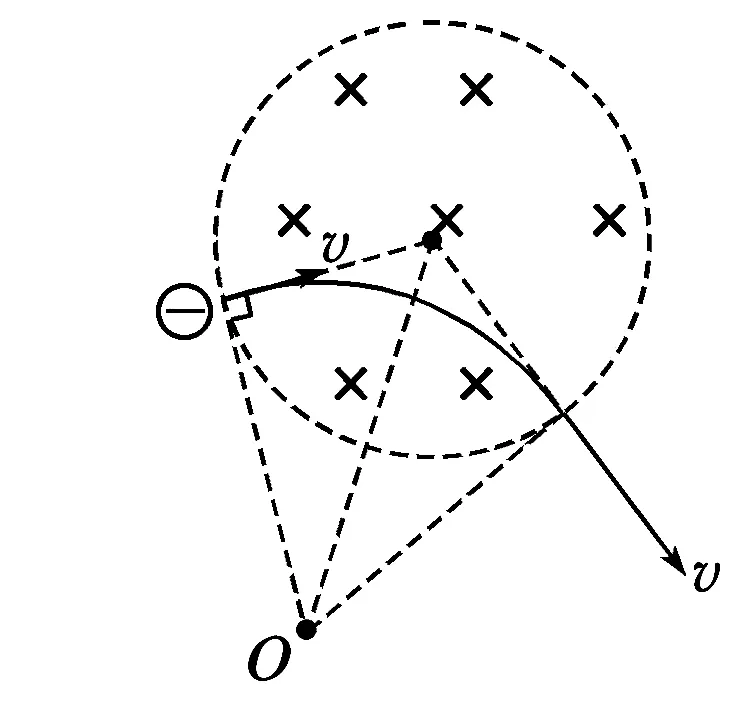
图3

3.在圆形边界中

方程思想是高中物理解题的重要思想，其运用不仅仅局限于解题，通过方程研究问题的过程中我们还可以挖掘命题人的命题思路，尤其在高考题创新性增强的背景下，把解题思路还局限在以前的套路题中已无法满足高考的需求.这里我们可以将上述的方程简单归为三类：

基于基础物理学规律的方程牛顿第二定律;动能定理;动量守恒定律基于模型特征的方程杆绳连接体模型;船过河模型;木板滑块模型基于题目中已知的数量关系某天体质量为地球质量的n倍

学生在解题过程中也可以基于这三类方程对题目中的物理情景经行描述.

关于方程组的解，在高中物理需要计算的题目中，最后的计算结果大致分为两类，一类是求出某个物理量的具体值，对于这一类问题当方程组中未知量的数量与方程的数量相同时便可求解.另一类是计算两个物理量的比值，对于这一类最后列出的方程组中未知量的数量会比方程的数量多，这种情况下计算结果将会存在比值.

老师通过研究方程思想可以帮助自身梳理教学思路，另一方面也可以提升老师自身命题的能力，使越来越多的原创题出现在学生的试卷中.