难道变量分离法用错了吗
俞新龙
(浙江省绍兴市柯桥区越崎中学 312050)
一、一个教学片断
在变量分离法教学时,我先让同学们做了下面这道




综上,a≤1-2ln2,从而实数a的最大值为1-2ln2.
上面每一种情况的讨论不能出任何差错,否则必将前功尽弃!但如果我们用变量分离的方法解该题,则将容易得多.
我们知道变量分离法解决一些求参数范围的问题效果非常好,如上面的引例.正是基于对变量分离法解决参数范围问题的信心,所以我们大都对它情有独钟,在遇到求参数范围问题时,一般都会先试着用变量分离法尝试做一下.接着我让同学们做了下面这道题:
题1若函数f(x)=x3+x2-ax-4在区间(-1,1)上恰有一个极值点,则实数a的取值范围为____.
原问题等价于f′(x)=3x2+2x-a在区间(-1,1)上有一个根,解决方法和答案集中在如下两种:

解法2(函数零点存在定理):f′(-1)f′(1)=(1-a)(5-a)<0,解得1 题2若函数f(x)=ax2-x-1有且仅有一个零点,则实数a的取值范围为____. 该题同学们用两种方法给出了相同答案. 从对比题的解答情况看,大家形成2点共识:题1的情况不是一元二次函数问题因素造成的,也不是变量分离法造成的.虽然原因还没找到,但大家一致认为应该往极值方面找原因.看来离真相不远了.于是我让同学们继续完成下面问题. 题3已知函数f(x)=x3+ax2+bx+a2在x=1处有极值10,则a+b=____. 上述做法得到部分同学的反对,这些同学指出当a=-3,b=3时,f′(x)=3(x-1)2≥0,所以x=1处函数f(x)无极值.出现了与题1相同的情况!此时,同学们都做恍然大悟状,大家都知道了题1错误的原因是:f′(x0)=0是函数y=f(x)在x=x0处取到极值的必要而不充分条件,即存在函数满足:在某点导数为0,但不是这个函数的极值点,如题1、题3等.当然,题1的导数是一元二次函数也起到了推波助澜挖坑的作用,因为在有关极值问题中,两个等根不应该视为一个根. 问题虽然解决了,但我们知道,在高中数学中类似的情况还有许多,于是,我又让同学们归纳总结、整理了一些易错的或易忽略的知识点,如空集、函数定义域等等,并课堂练习如下习题: 练习结束后我还向学生补充以下解法: 教学是一项系统工程,如何开展教学比较好,没有固定的模式,也不可能产生模式,因为每一次教学都会随着学生的不同、教学内容的不同、教学情境(情况)的不同而变化,即每次教学都是新的,但教师应努力追求一种最适合学生的教学方法,让他们在充满“趣味性”的教学情境或教学载体中获得知识.数学家哈尔斯说过:“问题是数学的心脏.” 著名数学家波利亚还说过:“一个专心、认真备课的老师往往能够拿出一个有意义但又并不复杂的题目,去帮助学生挖掘问题的各个方面,使得通过这道题,就好像通过一道门,把学生引入一个完整的理论领域.”这就要求教师平时必须做一个有心人,要留意哪些问题能成为帮助学生寻找到“更多周围蘑菇”的“蘑菇”. 在教学中常会遇到“讲过做过的数学问题、方法”学生又做错了或不会了的情况,那么如何来保障教学的有效性和长效性呢?我们知道,只有当知识在学生最近发展区并符合认知规律时才易于被学生接受而内化为他(她)自己的知识,类似本文情况实际上就是教师教学中缺少让学生主动建构知识造成的,所以教师应根据知识掌握的不同要求采用讲授式、体验式、矛盾式等多种教法让学生经历头脑风暴,并根据遗忘规律“三天小提醒七天大提醒”的形式开展教学. 每次教学随时会出现意料之外的情况,具有不可预测的可变性,时时刻刻考验着上课者的生成性教学能力.这就要求教师在平时备课时要多预设可能发生的情况,提前做好各种预案,“台上一分钟,台下十年功”.教师只有深入题海,才能了解问题出现的各种可能情况和处理方式,才能冷静思考、处变不惊的处理好生成教学.





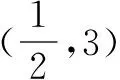
二、由此引起的一些教学思考

