自锚式悬索桥吊索力缺失分析
蒋俊秋,刘祥宇,陈桂成
(1.重庆交通大学 土木工程学院,重庆市 400074; 2.重庆中设工程设计股份有限公司)
近年来,自锚式悬索桥作为一种新的桥梁结构形式,由于其具有不需要设置庞大的地锚、对地基要求相对较低等优势,成为中小跨桥梁结构中的热门桥型。
自锚式悬索桥是一种自平衡体系,其受力变化比地锚式悬索桥更复杂。目前国内外针对地锚式悬索桥的研究已经相对成熟,而对自锚式悬索桥的研究较少。故应结合自锚式悬索桥结构特点,对其进行进一步研究。对于自锚式悬索桥这一类缆索桥梁,随着时间的推移难免会出现索力缺失的情况,从而影响整体结构受力。与新桥修建时缺乏吊索不同:一方面,自锚式悬索桥修建时有各种临时设施保证施工阶段的结构受力与安全,而后期吊索力缺失时没有这些临时设施;另一方面,新桥修建时吊索是按照特定的顺序进行张拉,而后期吊索力缺失具有随机性,两者之间受力模式有所区别且前者更不利于结构受力。因此,有必要对其吊索力缺失进行分析。
在自锚式悬索桥索力缺失情况中最不利是断索(即吊索力损失100%),而其他索力损失的情况(如锚头松动,吊索松弛、老化,以及施工过程中各种因素可能会对吊索损失产生的影响),可按其索力损失的比例,参考断索情况进行插值参考计算。同时,由于多根吊索的断裂可由单根吊索依次进行叠加计算(各吊索断裂处索力为零)。因此,该文仅以自锚式悬索桥中出现单根吊索断裂的情况为例进行计算分析,多根吊索力缺失可参照此方法进行逐一叠加计算。
该文旨在分析自锚式悬索桥的索力缺失对全桥结构的影响,通过理论推导,得到相应理论解,完善自锚式悬索桥设计理论并对结构的优化设计提供参考。
1 计算原理
该文考虑缆-梁联合作用,将自锚式悬索桥拆分为主缆与加劲梁两部分独立分析,两者通过吊索的变形协调条件进行耦合,如图1所示。

图1 计算方法原理图
令原成桥状态为工况1,去掉某一吊索后状态为工况2。
主缆部分主要通过工况1给定的各吊点间索段的无应力长度以及吊索间距,求得满足工况2要求的主缆线形,同时求出工况2状态下,主缆端部反力、吊索索力。
将加劲梁从整体结构中分离出来采用膜理论进行分析。忽略梁体剪切变形、吊索的伸缩和倾斜变形对结构受力的影响,将离散的吊索力简化为连续的均布荷载,作用于加劲梁上。因此,吊索力损失可简化为加劲梁相应位置所增加的附加荷载,将其直接施加于加劲梁上,得到吊索力损失后加劲梁所受的附加弯矩、挠度变形等。
2 主缆的几何非线性分析
在考虑主缆非线性分析中,主缆的弯曲刚度可忽略不计,吊索力、索夹自重都以等效集中力Ti′方式作用在其相应位置上,并注意到计算的是主缆有应力平衡位置,其变形已基本完成,因此在主缆计算过程中不伸长。
如图2,取主缆吊索间一段无伸长的自由悬索,其坐标为yi向下为正,单位缆长重为q,任一处的Lagrange坐标为s,相应笛卡尔坐标为(x,y),则任意索自由索段端点力与坐标之间的函数关系需满足:
(1)
(2)
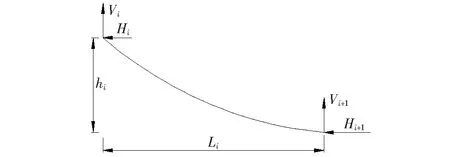
图2 索形力学模型简化图
吊索间任一索段都必须满足式(1)、(2),令Vi=V,Hi=H,于是:
(3)
(4)
式中:Li为i号梁段吊索间距;Hi为i号梁段主缆吊点高差;si为i号梁段主缆无应力长度。
成桥状态有:
(5)
通常情况下有:Lm-1=Lm
对仅有垂直吊杆的情况:
Vm=Vm-1-(Tm+qsm-1)
(6)
3 主缆分析
3.1 主缆方程的求解
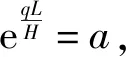
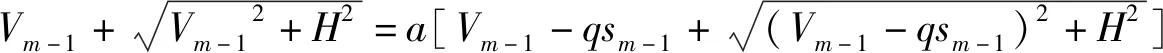
(7)
故,可令:
Vm-1=a(Vm-1-qsm-1)+x,可得:
(8)
(9)
将式(8)代入式(9):
(10)
整理可得:
4a2x2+4a(Vm-1-qsm-1)(a2-1)x-(a2-1)H2=0
(11)
将式(8)代入式(11),整理得:
4a2x2-4aqsm-1(a+1)x+(a2-1)H2=0
(12)
此方程的解为:
(13)
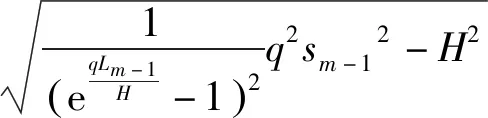
(14)

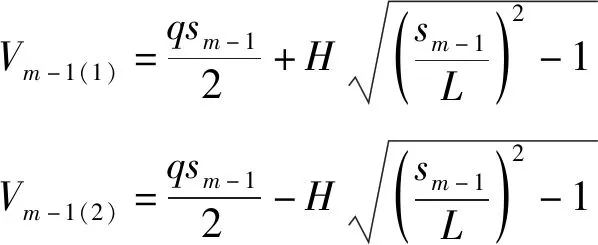
(15)
对Vm-1有如下取值:
若hm-1>0时(m-1梁段主缆吊点左高右低):
(16)
若hm-1<0时(m-1梁段主缆吊点左低右高):
(17)
3.2 主缆水平分力变化分析
索力损失后,(m-1、m)节段合二为一,如图3所示。参考结构力学中位移法的思想,采取如下方法进行求解:
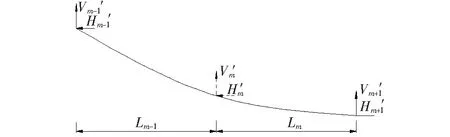
图3 工况2索形力学模型简化图
(1) 首先取出(m-1、m)节段,并将m-1、m两点固定[固定后(m-1、m)节段受力变化不影响主缆其他节段],即:主缆Vi通过(m-1、m)节段前后与原成桥状态保持不变。
(2) 令原成桥阶段m点处的吊索力为Tm,由于主缆竖向分力V的变化与其节段无应力长度呈线性关系,故将Tm按主缆节段无应力长度进行分配,显然可得:
由式(16)可得:
正是由于Tm的改变使得H、V发生了变化。
易知:
Vm-1=qsm-1+Vm+Tm
(18)
(19)
可得:
(20)
(21)
(3) 根据上述分析,固定m-1、m两点后,m-1、m两节段主缆水平分力应满足式(21);对于主缆的其他节段,应满足式(20)。
去掉m-1、m处固定约束后,自锚式悬索桥各主缆节段间相互连续,整个主缆所受的水平分力H′应处处相等。因此,对式(20)、(21)进行修正。
(4) 主缆各节段水平方向刚度与其主缆节段矢跨比有关(可以认为主缆节段水平刚度与相应主缆节段水平分力线性相关),因此,可将式(20)、(21)中的主缆水平分力按其相应主缆节段间的水平距离以及水平刚度进行分配。
对于吊索等间距的情况,可令主缆总共分为n个节段,故有:
(22)
(23)
通过式(23)可知:索力损失后吊索水平分力较原成桥状态有所下降。这是由于吊索力的损失,对主缆来说,相当于卸载,导致主缆内力减小,从而使其水平分力减小。
索力损失对主缆影响程度与自锚式悬索桥主缆被吊点分割数n(表现主缆与加劲梁联系的紧密程度,联系越紧密影响越小)、索力损失处吊点原成桥阶段竖向分力Vm与损失的吊索力Tm及其主缆相邻节段无应力索长sm-1与sm密切相关。
自锚式悬索桥主缆、加劲梁共同承担荷载,荷载不变的情况下,主缆受力的减小势必会增加加劲梁的受力、变形。其中,当主跨跨中吊索力出现损失时,加劲梁产生的挠度、附加弯矩最大,对加劲梁最不利。
4 吊索、加劲梁分析
4.1 吊索力分析
吊索力缺失后,缺失点附近主缆节段的水平距离必然会发生变化,因此,不能直接进行计算,应采用如下方法分析(令n#吊点索力缺失):
(1) 根据自锚式悬索桥主缆位移的弱相干性,用缺失后的主缆水平分力H′替换原水平分力H1代入式(6)、(15),计算得到一组新的吊索力Ti′,同时将n处的Tn′根据其相邻主缆节段无应力长度分为Tn′L与Tn′R(Tn′=Tn′L+Tn′R)。
(2)n#吊点左侧吊索力分析。
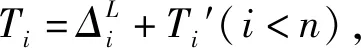
故有:
因此,可得:
(24)

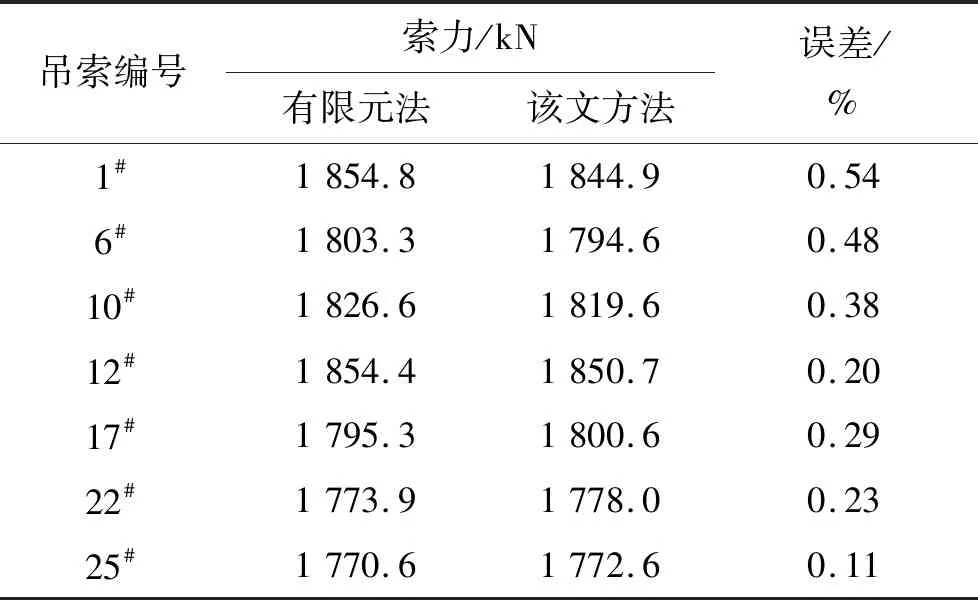
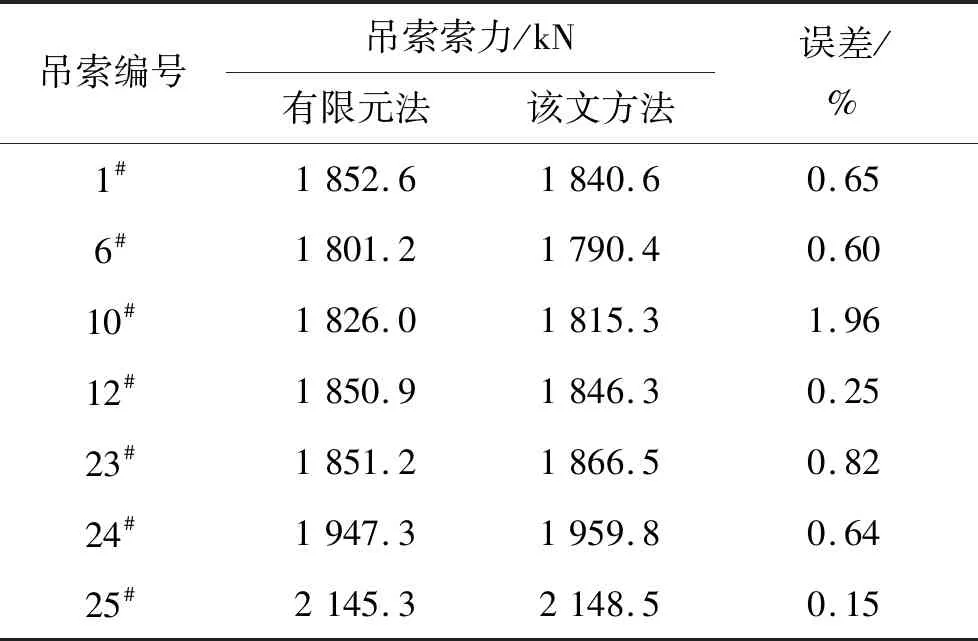
从而通过式:Ti=ΔiL+Ti′(i n#吊点右侧各吊索力参照步骤(2)进行计算,不再赘述。 由于加劲梁受力与普通梁的受力相类似,具有较大的刚度,且吊索力分布较为均匀,可对加劲梁在吊索力缺失的受力进行近似分析: 考虑加劲梁整体模型,忽略梁体剪切变形、吊索伸缩以及倾斜变形对结构受力的影响,将离散的吊杆简化为一连续膜。 成桥后,加劲梁主要受自重荷载qc(方向向下)、吊索力荷载qp(方向向上)以及主缆水平分力H′共同作用。对于竖向荷载,由于吊索力分布基本均匀,可视为均布荷载,故作用于加劲梁上的荷载为: q′=qc-qp 图4为某3跨自锚式悬索桥加劲梁受力图示(边跨跨径为l1,中跨跨径为l2,令l2=al1)。 图4 自锚式悬索桥加劲梁受力图示 图5 索力损失后加劲梁受力图示 根据之前的分析可知:跨中吊索力损失对加劲梁最不利。因此,以跨中吊索力缺失为例,分析加劲梁受力情况(取加劲梁无预拱度的情况)。 由于加劲梁受力是线性的,可在原成桥状态的基础上求得各附加荷载后根据力的叠加原理,将各附加荷载分别进行叠加,如图6所示。 图6 加劲梁所受附加荷载图示 其中Δq=qp-qp′,考虑到吊索间距Li《l2,可以将原跨中的均布荷载简化为一集中荷载F进行近似分析,F=(qc-Δq)Li-2ΔT′,见图7。 图7 加劲梁所受附加荷载简化图示 通过位移法求得图7结构弯矩图,如图8所示。 图8 加劲梁所受附加荷载弯矩图(1) M1~M6即为跨中吊索力损失后竖向荷载作用下加劲梁所增加的附加弯矩,与加劲梁水平荷载产生的弯矩相叠加即可得到其最终附加弯矩,令l2=al1。 取图8所示坐标系: 可得: (25) 式中: 取图9所示坐标系: 图9 加劲梁所受附加荷载弯矩图(2) BC段弯矩为: BC段边界条件(根据转角连续性): (26) 式中: 由此,在分析吊索力缺失对加劲梁整体受力影响时,将索力缺失转换为附加荷载作用于加劲梁上,并与加劲梁原受力状态进行叠加,从而得到其受到影响后的最终状态。 此外,由于加劲梁所受的吊索力并非完全的均布荷载(具有离散性)。因此,在对其进行弯矩、剪力计算时,应根据各吊索力进行求解。同时,加劲梁为压弯构件,在计算时须对其进行稳定分析,通过对各加劲梁节段进行分析可知:加劲梁上各吊点对加劲梁会产生约束作用,有利于加劲梁的稳定;某吊点索力缺失后,缺失点附近节段合二为一,其有效计算长度增加,稳定性变弱。 由于受到各方面因素的影响(如吊索先天缺陷、管养不到位、锈蚀等),可能会引起吊索有效截面的减小,从而引起吊索力发生变化影响全桥受力。 此类工况可进行简化分析,根据先前的结论,吊索力发生变化时,取相应吊索对应的部分节段进行分析。 当n#吊索有效截面出现缺失时: (1) 首先,固定n#吊索对应的主缆以及加劲梁节段吊点,使得该处主缆、吊索、加劲梁各部分间受力变化互不影响。同时令n#吊索有效截面积减小后与先前之比为v,且该吊索原索力为Tn。 此时,主缆、加劲梁线形与n#吊索有效截面缺失前一样,因此在n#吊索主缆与加劲梁吊点处对应的吊索力为Tn;对于n#吊索,由于其有效截面与原截面之比为v,且吊索索长未发生变化,因此,在此状态下n#吊索的索力为vTn。 (2) 释放n#吊索对应的固定约束,由于Tn>vTn,此时,主缆、吊索、加劲梁吊点处吊索力重分布,从而达到平衡。 在此过程中,相应主缆吊点向上移动,加劲梁吊点向下移动,吊索伸长,即n#吊索所对应的主缆与加劲梁吊点处对应的吊索力由Tn减小,n#吊索力由vTn增大。达到平衡时,Tn′∈[vTn,Tn)。 由之前的分析可得,吊索力缺失,对主缆来说相当于卸载,且对加劲梁会产生不利影响,应重点分析此类工况对加劲梁的影响。出于对桥梁设计偏安全考虑,可取Tn′=vTn,根据前文的等效附加荷载分析插值进行计算。 该文考虑自锚式悬索桥的缆-梁联合作用,将自锚式悬索桥拆分为主缆与加劲梁两部分独立分析。 对于加劲梁部分,由于其刚度较大,且材料均处于弹性阶段,满足线弹性理论与叠加原理,因此,可根据吊索力的实际损失与其断索时的计算分析对其进行线性插值。 对于主缆部分,虽然其受几何非线性的影响,但针对单根吊索的索力缺失对主缆整体影响非常有限。可认为,单根吊索力缺失对主缆结构的影响是满足线性理论的,可根据此吊索力的实际损失与其断索时的计算分析对其进行线性插值。 针对实际工程中可能出现的多根吊索力缺失情况,计算时应逐一对每一根吊索进行迭代计算,不可直接叠加。 某自锚式悬索桥,跨径布置为(150+406+150) m,边跨索距为(14.5+9×13.5+14) m,加劲梁锚固点与主缆理论顶点高差85 m;中跨索距布置为(14+28×13.5+14) m。 加劲梁:惯性矩I=4.428 675 m4;弹性模量E=2.1×105MPa;一期+二期恒载q=132 kN/m。 主缆:截面面积A=0.103 8 m2;弹性模量E=1.95×105MPa;主缆自重q=8.145 kN/m;矢跨比f/L=1/5.8。 为了简化计算,忽略索夹及吊索自重,且不作索鞍修正,仅以主缆理论顶点计算,经过计算,其成桥阶段主缆水平反力为H=40 433.8 kN,取其主跨分析,如图10所示。 图10 某自锚式悬索桥总体布置图(单位:m) 以跨中26#吊索断索(索力缺失100%)为例,分析索力缺失对自锚式悬索桥结构的影响。 原成桥状态初始水平分力通过式(20)计算。 根据算例条件可得: q=8.145 kN/m s25=13.503 4 m T26=1 767.7 kN L=13.5 m 代入式(20),可得: 有限元计算: H1=40 980.6 kN 故有: 通过H、si、q、Li按各主缆节段分别计算,得到各吊索力如表1所示。 (1) 吊索缺失后水平分力计算 跨中吊索力缺失后,主缆水平分力通过式(22)计算。得: 表1 吊索力计算结果对比 H1′=40 926 kN 故有: 吊索力缺失后,主缆水平分力稍有减小,主缆整体受力减小。 (2) 吊索力损失后吊索力计算 计算可得跨中吊索力缺失后,各吊索力如表2及图11所示。 表2 索力缺失后吊索力计算结果对比 图11 吊索力分布图 (3) 索力缺失对加劲梁影响近似计算 计算图示见图12。 图12 加劲梁所受附加荷载图示 根据4.2节分析,可得,qp=qc=132 kN/m。同时,将之前所计算的索力缺失后各吊索力(除缺失点相邻吊索)进行均摊,可得qp′=131.708 kN/m。 因此,可得: H′=41 490.986 kN ΔT=874.793 kN Δq=qp-qp′=0.292 kN/m F=(qc-Δq)Li-2ΔT′=28.472 kN yc=0.046 m 有限元计算: yc1=0.047 m 根据索力缺失后各吊索具体索力对加劲梁进行分析,得到索力缺失后加劲梁剪力图、弯矩图如图13、14所示。 由图13、14可知: 图13 加劲梁剪力图 图14 加劲梁弯矩图 (1) 吊索力缺失后,主缆水平分力稍有减小,主缆整体受力减小。 (2) 跨中吊点相邻两侧附近吊索力明显增大,而远离索力缺失点的吊索力较原成桥状态有所减小;跨中吊索缺失后其相邻吊索力增大20%~30%。 (3) 虽然加劲梁在索力缺失的吊点处出现较小的挠度,但加劲梁弯矩较成桥状态有较大变化,且加劲梁稳定性变差,应引起重视。其受力变化与加劲梁边中跨比、加劲梁材料与结构形式以及吊索力及分布有关。 此外,索力损失对自锚式悬索桥受力、变形影响还与主缆与加劲梁联系的紧密程度相关。主缆加劲梁联系越紧密,式中n越大,索力缺失所造成的影响越小,反之,则越大。 综上所述:该文计算方法准确、可靠、满足精度要求。公式化的近似理论解,对完善自锚式悬索桥设计理论,提高对结构整体力学性能的把握具有参考价值。 (1) 基于分段悬链线理论及膜理论提出自锚式悬索桥成桥阶段以及吊索力缺失影响分析方法,可准确分析自锚式悬索桥成桥阶段受力以及吊索力缺失后桥梁结构的受力与变形。 (2) 考虑缆-梁联合作用,对分段悬链线理论方程结合自锚式悬索桥受力特点进行求解,考虑非线性,得到主缆节段受力的近似理论解,在此基础上,对结构吊索力缺失的各种情况进行分析,为完善自锚式悬索桥设计理论,提高对结构整体力学性能的把握具有参考价值。 (3) 从计算方法、过程及结果与有限元法对比可以看出:该方法较为可靠,精度较高;公式化的计算方法,便于对结构进行理论分析以及编程计算,简化了自锚式悬索桥非线性计算。4.2 加劲梁受力近似分析

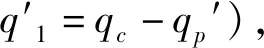



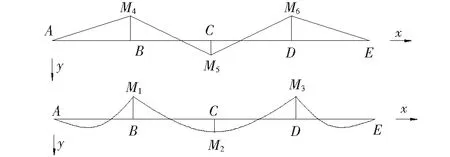
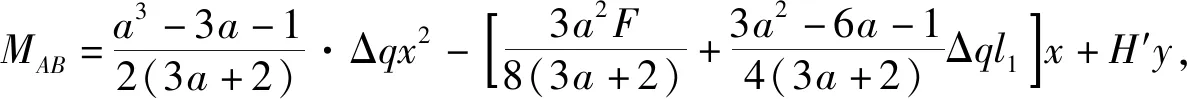

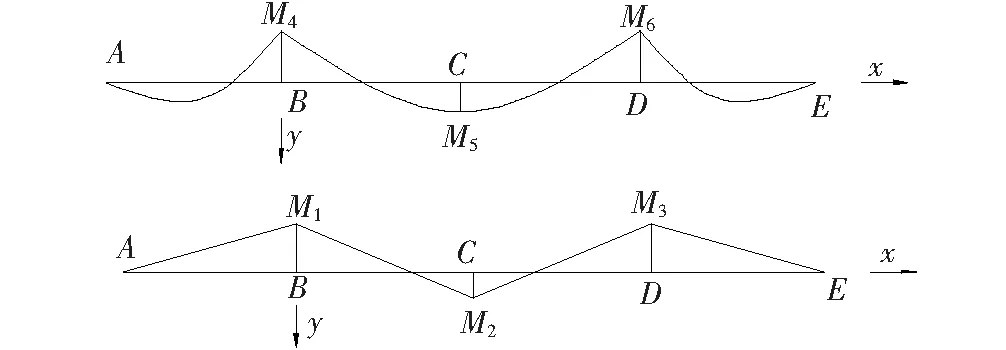
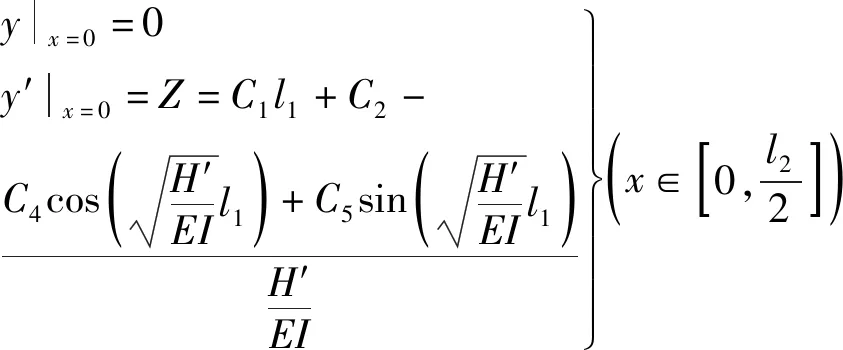
5 其他吊索力缺失与插值计算
5.1 吊索有效截面减小
5.2 吊索力缺失的插值计算
6 算例分析
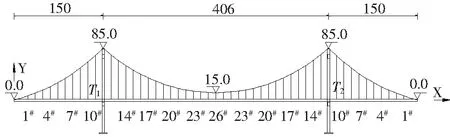
6.1 由成桥状态验证上述计算方法
6.2 吊索力缺失分析
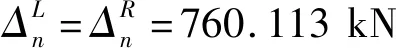
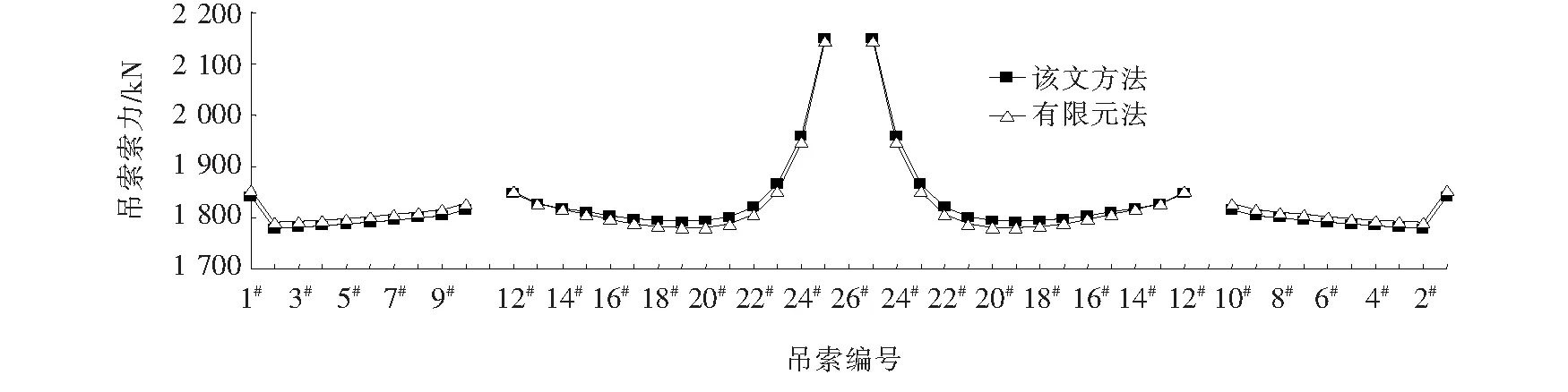

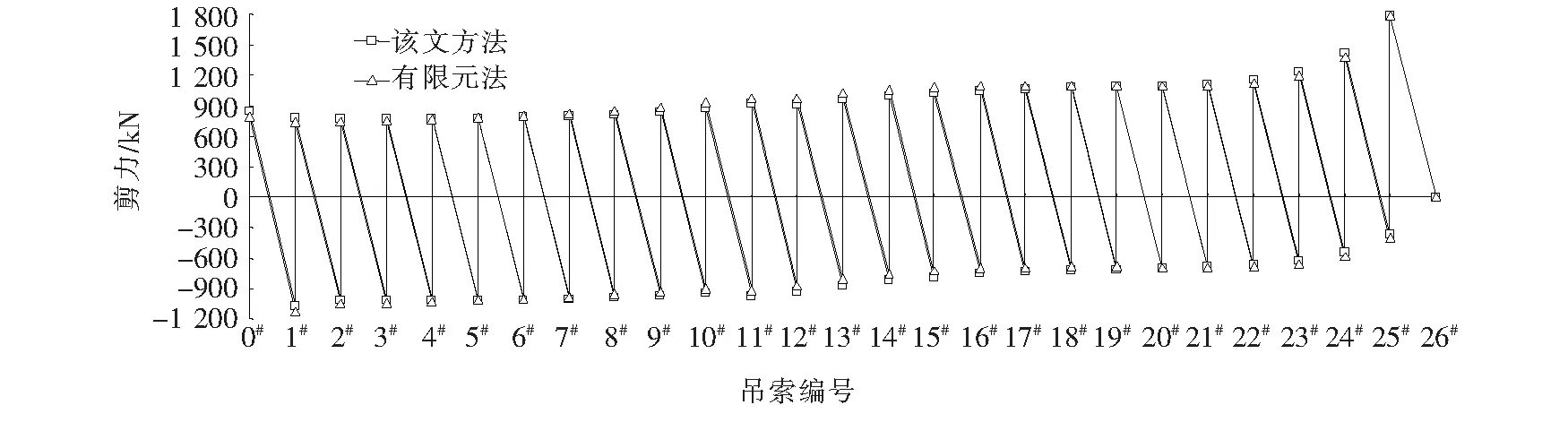
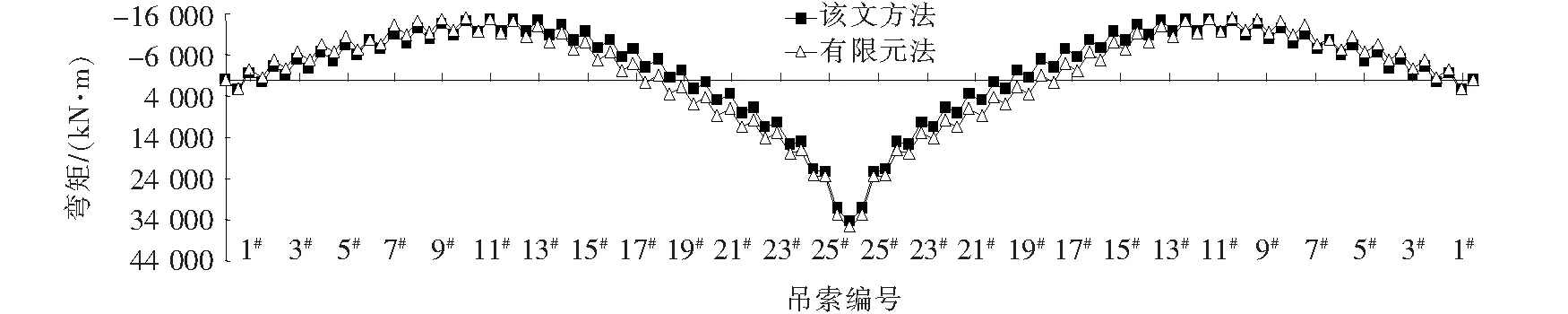
7 结论

