基于分数阶拓展算子GM(1,1)模型的高速公路养护成本预测

向红艳, 徐莲怡

(重庆交通大学 交通运输学院，重庆市 400074)

随着中国高速公路里程的快速增长，未来将全面进入高速公路网络化运营。高速公路的大量建设必然带来后期巨大的公路养护和维护任务。该文通过对历年高速公路养护成本数据的分析，尝试对养护成本的复杂性和随机性进行研究，探索各类别养护成本的变化趋势，对未来的养护成本进行预测。对高速公路运营管理具有重要意义，有利于成本管理从事后核算向事前、事中控制逐步转变。

目前，国内外研究人员在高速公路养护成本预测方面开展了广泛的研究。朱合利等运用系统工程学方法，对高速公路养护成本影响因素进行了识别，构建了养护成本分析的解释结构模型(ISM)和多级递阶因素结构模型，对成本要素的逻辑关系进行了研究；于英等运用边际成本原理，将高速公路划分为若干单元，建立了高速公路交通流量、道路长度、车道数、匝道数、材料设备与养护成本之间的多元回归分析数学模型，结果表明，养护成本随交通流量和道路长度成对数变化；邱兆文等在高速公路养护费用测算方法中，构建了养护维修率指标体系，提出了基于综合路况的单公里养护维修费用计算模型，为养护经费的合理分配提供决策依据。

上述模型对养护成本的构成和影响因素进行了充分研究，但由于影响因素的量化和数据收集十分困难，模型精度有限。该文基于大量历史成本数据，运用灰色模型处理数据，建立更为精准的养护成本预测模型，以利于解析养护成本的变化趋势，提高预测精度。

1 高速公路养护成本的特征分析

高速公路建设的技术标准高，其养护工作涉及面广、工作量大，往往需要使用多种设备，机械费用高，以上因素造成高速公路养护综合成本较高。随着高速公路运营时间增长，交通量逐年增加、大型货车超载行驶，对高速公路的破坏不断增多，给养护工作带来很大困难。

1.1 养护成本构成分析

高速公路养护是对路基工程、路面工程、桥梁隧道工程、交通工程、绿化工程、收费设施工程等附属设施的养护，通过养护维修保养使得高速公路达到较好的服务水平。通过多部门数据进行汇总整理，按不同性质归类口径，形成有研究价值的成本数据。主要养护成本可分为：公路日常养护成本、公路专项中修养护成本、公路大修养护成本3类，其养护分类、养护主要内容、特点见表1。

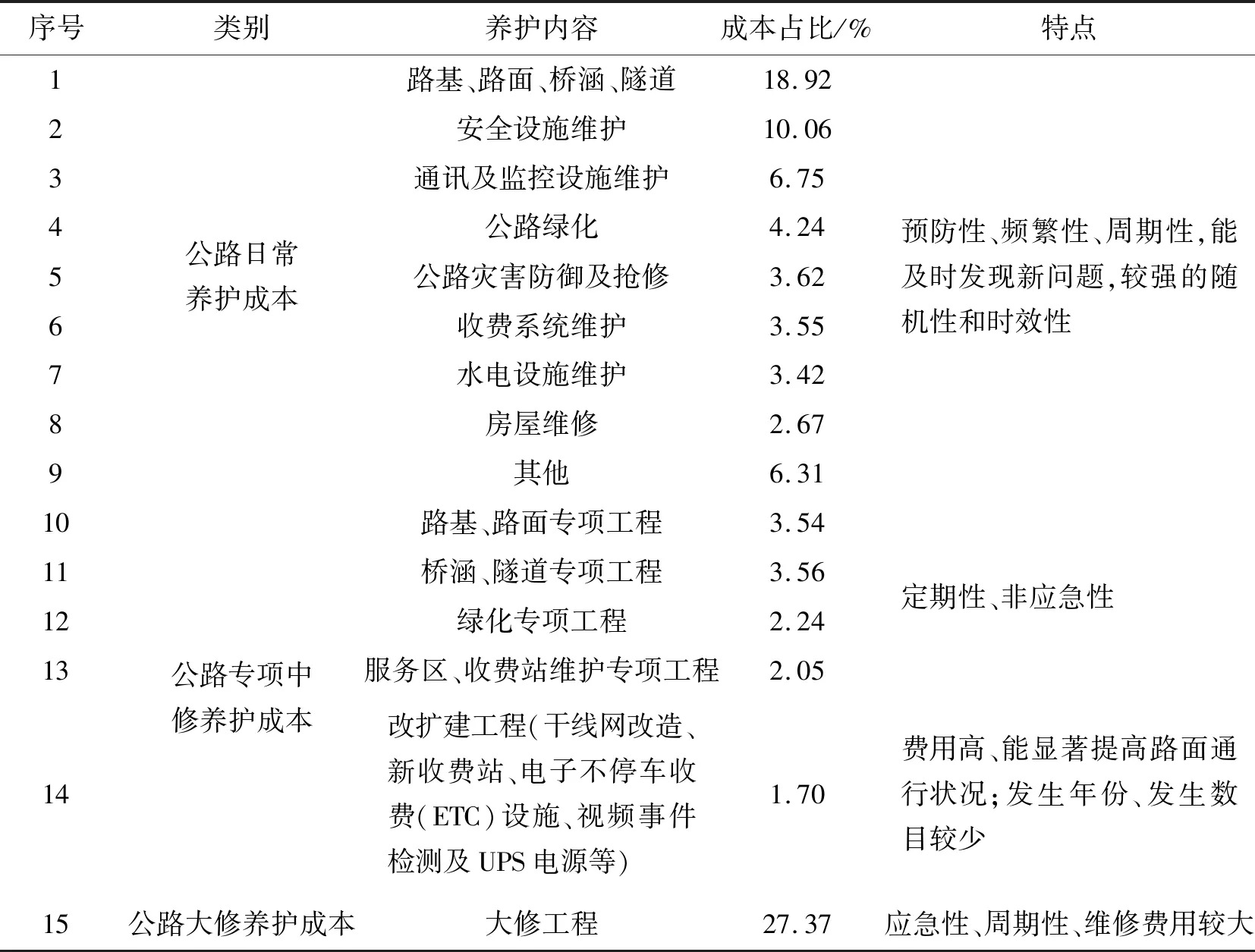
表1 高速公路养护成本的构成分析

1.2 养护成本变化趋势及特征

高速公路投资周期长，为了使高速公路保持一定的服务水平，在公路运营期间，需不断投入资金，对公路进行定期的日常养护与大、中修养护。高速公路养护成本具有大规模、多类别、低价值密度和多变化等特点，其成本构成复杂、涉及面广、影响因素较多。

(1) 日常养护费用特征

一般情况下，公路运营初期，车流量较小，无专项中修、大修养护成本支出，日常养护成本的路基、路面、桥涵、隧道的养护费用呈逐年缓慢增加趋势，占日常养护费用约30%，安全设施维护占日常养护费用约20%，公路灾害防御及抢修费用仅在发生年限支出，具有不可抗性和不可预测性。

(2) 专项中修费用特征

随着运营年限增长，交通量亦快速增长。高速公路病害越来越多，需定期对公路进行专项中修，专修费用在总养护费用中所占比例越来越大。专项中修所产生的费用跟交通量、建设时期的技术水平、施工水平、材料及养护管理水平有关。

(3) 大修费用特征

大修工程费用一般在公路运营10年后产生，随着运营后期高速公路及其附属设施达到其服务周期，一般按照12～15年一次的频率考虑综合修理，使之全面恢复至原设计状态。

2 基于分数阶拓展算子的养护成本预测灰色模型

2.1 建模思路

高速公路养护成本预测，其影响因素十分复杂，且数据在记录过程中存在计算误差、人工误差、设备误差等多种误差。灰色预测模型在应对数据缺失或信息不足方面，较之其他预测方法具有先天的优势，对高速公路大数据养护成本预测优势更为明显。

灰色模型是邓聚龙教授于1984年首次提出，随后陈锦云、刘思峰、李宝林、宋中民、王义闹、谢乃明、王正新、崔杰等研究人员以经典GM(1,1)模型为基础，将单序列拓展到多序列，将一阶拓展到多阶，形成以GM(n,h)模型为主要类型的灰色预测模型。如今，灰色预测模型灰色预测已经在农业、工业、社会、经济、交通、能源、医疗等众多领域得到广泛应用，成功地解决了生产、科研、管理中的大量现实问题。灰色模型是通过对原始数据的挖掘、整理来寻求其变化规律，避免了各因素之间的影响，只考虑总体的发展趋势，且灰色序列生成可弱化表象复杂、数据离散的客观系统的随机性，挖掘出其蕴含的内在规律。高速公路养护成本影响因素多而复杂，考虑成本的构成体系、各因素对成本的影响，以历史数据为基础，通过对数据关联性和内在特征的分析，提取有显著规律的成本初始数据，采用分数阶拓展算子的灰色预测模型，得到精度更高的预测结果。建模过程中设置调节分子阶数和迭代算法，不断生成新的目标成本序列，并多次迭代得到预测结果，可大大提高养护成本预测值的准确度。

2.2 养护成本预测建模

基于灰色理论的养护成本预测算法是将实测数据X(0)作为输入，将X(0)的r分数阶累加生成序列X(r)进行均值处理后的Z(r)作为建模数据，X(r)预测值经过r分数阶累减还原为原始序列X(0)的预测值。

假设X(0)={x0(1),x0(2),…,x0(n)}为原始养护成本数据，其中n为序列长度，对其进行r阶累加生成处理：

X(r)={x(r)(1),x(r)(2),…x(r)(n)}

(1)

其中：

(2)

x(r)(k)+ax(r)(k)=b

(3)

当r=1时，x(0)(k)+ax(r)(k)=b变为x(0)(k)+ax(1)(k)=b。

使用X(0)的r分数阶累加生成序列X(r)、进行均值处理的Z(r)={z(0)(1),z(0)(2),…,z(0)(n)}作为建模数据，其中：

(4)

x(r-1)(k)+az(r)(k)=b

(5)

当r=1时，x(r-1)(k)+az(r)(k)=b变为x(0)(k)+az(1)(k)=bX(-r)={x(-r)(1),x(-r)(2),…,x(-r)(n)}为X(0)的r阶累减生成算子，其中：

(6)

2.3 参数标定

(7)

其中Y、B分别为：

(8)

(9)

分数阶拓展算子GM(1,1)模型x(r-1)(k)+az(r)(k)=b的时间响应序列为：

(10)

还原值为：

(11)

(12)

2.4 预测效果评价

为评价模型的预测效果，该文运用结果比较法，即通过观测数据与预测数据相比较，计算预测误差。设ε(k)表示预测误差，则：

(13)

令Δk为相对误差，Δ为养护成本序列的平均相对误差，则x(0)(k)序列的平均相对误差检验公式为：

(14)

(15)

令S(X)为序列均方根误差，则x(0)(k)序列的均方根误差检验公式为：

(16)

3 实证分析

3.1 数据来源

以某高速公路历年养护成本数据为例，按照1.1节中所述成本结构进行统计。得到18类共8年的数据。利用缺失数据填补和异常数据剔除等方法对数据进行预处理，得到初始成本时间序列。选取数据样本较多且具有周期性变化的日常养护成本数据，除去具有不可抗性的公路灾害防御及抢修和其他两类成本，剩余10类成本分类数据见表2。利用10组数据建立灰色预测模型，得到预测结果并分析。

3.2 预测结果及分析

以路面养护成本预测为例，取r=0.9，用分数阶拓展算子GM(1,1)模型对其进行模拟，得：X(0.9)={21.80,199.78,199.76,297.65,418.09,553.56,707.13,846.59}；计算发展系数和灰色作用量，取a=-0.094 5，b=81.100 4，计算GM(1,1)模型对应的微分方程，得：

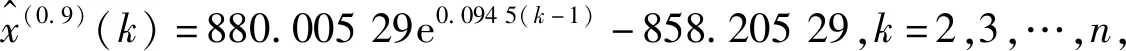
表2 相关养护成本数据

表3 预测结果及误差分析

由表3可知：r=1的GM(1,1)模型平均相对误差、均方根误差略大于r=0.9的分数阶拓展算子GM(1,1)模型。总体来说，经过残差检验，分数阶算子GM(1,1)模型预测精度都达到了合格标准，拟合精度较好，预测模型的可信度较高，可用此模型预测高速公路运营期养护维修保养费用(图1)。

图1 路面养护成本预测结果

由图1可知：分数阶拓展算子GM(1,1)模型对高速公路隧道养护成本的预测较准确。总体来看，路面维修保养费用不断增加，且递增幅度在不断提高。r=0.9时，2010年养护成本预测值与实际值误差最小，相对误差为0.68%；2015年预测误差较大，最大相对误差约为14.30%。预测结果为高速公路养护计划的制定与成本控制提供了科学依据。

4 结论

中国未来的高速公路养护任务重，难度高。该文通过建立多类别、结构化公路养护成本体系，分析成本的影响因素和特征。建立了基于历史数据的高速公路养护成本GM(1,1)灰色预测模型，设计了分子阶数调整方法和预测迭代过程，其模型精度提高，并得到以下研究结论：

(1) 高速公路养护成本表现出明显的增长趋势，随着运营时间增长，递增幅度不断增大。

(2) 日常养护成本、专项中修成本、大修成本具有不同的变化趋势，与高速公路自身交通量构成、使用年限有关。

(3) 灰色GM(1,1)模型对路面日常养护成本的预测效果良好，初期预测误差较小，随着预测时间增长，精度下降。