结合纹理特征分析的图像风格转换网络

余英东，杨 怡，林 澜

（同济大学电子与信息工程学院，上海201804）

（*通信作者电子邮箱1013928041@qq.com）

0 引言

图像风格转换也称图像风格迁移，作为最近图像处理方面一个新兴的研究方向，得到了广泛的关注。图像风格转换旨在保证原图像语义内容不变的前提下，艺术化地转换成不同的风格，从而达到艺术再创作等目的。

虽然只是将图像的风格进行转变，但是风格是一个相当抽象的概念。不仅照片与绘画的风格截然不同，不同画家，甚至同一画家在不同时期绘画的风格都不一样。如何找到计算机能够运算并处理的方式，准确地描述出图像的风格，是这个方向的难点。

早期的图像风格转换被设定为纹理合成［1］问题，即在限制纹理合成的同时，从源图像合成纹理以保留原图像的语义内容。大量的非参数算法被提出以用于纹理合成，同时使用不同的方法来保留目标图像的语义结构。例如可以通过重新采样给定源纹理来合成新的自然纹理［2-5］。文献［4］中引入了一个输入输出图像的对应映射，其中包括目标图像的图像强度等特征，来约束纹理合成过程。而Hertzmann 等［6］使用图像类比将输出风格化图像转移到目标图像上形成了早期的图像风格转换。Ashikhmin［7］认为这个过程中，想要转换的风格是更加重要的，因此他专注于传输高频纹理信息，同时保留目标图像的粗略尺度与语义。Lee等［8］改进了上述算法，通过边缘方向信息来控制纹理的转换。

自2006年深度学习［9］提出以来，在图像处理的许多方面，基于深度学习的算法已经成功超越了传统的机器学习算法。利用深度学习来把控图像的风格，结合利用损失函数的收敛来进行图像风格转换的研究进入了人们的视野。由Gatys等［10］提出利用深度网络等计算出的图像Gram 矩阵在图像风格的表达方面效果良好，并提出了基于卷积神经网络的图像风格转换算法，这个算法的核心思想激起了图像风格转换研究的热潮。Johnson 等［11］和Ulyanov 等［12］各自训练了一种前馈生成网络，用于快速的风格转换，但牺牲了转换的效果。而为了改善网络的风格转换效果，涌现了许多新的研究工作，Selim 等［13］利用空间约束来限制风格转换区域，从而提升转换目的性，避免转换不必要的区域；Li等［14］专门训练了一个利用WCT（Whiten-Color Transform）来进行照片的风格转换，但在绘画方面效果不佳；Shen等［15］提出利用元网络（Meta network）来进行转换过程，能够大幅度降低转换耗时，但是鲁棒性不强，效果较为一般；而Gu等［16］则将统计学加入进来，利用特征的统计学特征从而利用解码器来重构图像来达到风格转换，但是这一方法对原图的内容会有改变，生成图质量不够稳定。Chen 等［17］转换思路提出了Stylebank 算法，通过训练高斯噪声收敛来达到生成新图像的目的。尽管该方法一定程度上改进了效果，但是每张图片的训练都要经历冗长的训练使得网络效率相对很低。

现有的图像风格转换算法在网络的算法与训练上下了很多功夫，增加了各种限制条件来优化网络训练，利用卷积神经网络为主体转换网络，进行了大量的卷积运算，网络的训练过程过于冗长；另一方面，在进行网络调试与训练的过程中比较盲目，难以发现输入图像特征对于输出图像效果好坏的影响。本文在Johnson 等提出的前馈快速图像风格转换网络中受到启发，结合Gatys 所提出的Gram 矩阵对于图像风格的优良表达，提出利用预训练VGG（Visual Geometry Group）网络［18］，结合残差网络（Residual Network）［19］的前馈图像风格转换网络算法，同时基于输入图像的纹理特征分析来探索输入图像对于输出效果的影响，从而调整网络参数提升图像的转换效果。相比于早期的纹理转换，本文利用深度学习的优点，提取图像更深层次的特征来表达图像的内容以及风格特征。不同于传统的利用卷积神经网络的算法，本文在注重转换效率的同时，通过重用已训练的风格数据，从而提高每次图像转换的速度。通过风格图与内容图的纹理特征分析，发现了风格图的信息熵、内容图的高阶矩对于转换效果的影响作用，通过改变网络训练参数来提升转换效果，并发现对于高阶矩更低的内容图，网络能获得更好的输出结果。

实验表明，本文所提出的算法与表现较好的Gatys 算法、Stylebank算法相比，利用预训练网络来进行损失函数运算，减少数据量，加快训练速度；基于图像纹理特征分析能够更有效、更有针对性地改善网络训练过程。整体网络在风格转换的效果上有明显改善，在转换的速度上获得显著提高。

1 相关研究与工作基础

自深度学习提出以来，在图像处理方面，涌现出大量的网络，如前馈神经网络、卷积神经网络、对抗生成网络等。各种网络在图像的处理上都表现出强大的性能，但在训练效率、擅长领域不尽相同。图像风格转换不同于传统的图像分类，选取合适的网络至关重要。

1.1 前馈图像风格转换网络

Gatys 提出的算法中，将卷积神经网络与预训练的网络结合，包括5 个卷积层与4 个池化层，通过最小化重构特征损失以及基于预训练网络得到的风格特征损失来优化网络，来进行风格的迁移。虽然他的方法得到了较好的效果，但是基本思想与早期纹理合成相同，优化过程中每一个步骤都需要前向和后向通过预训练网络，导致计算量特别庞大。而改进的相关算法中，如Stylebank 利用高斯噪声迭代收敛来减少计算量，缩短训练时间，但是效果上不及前者。

为了能够在保证转换效果，又一定程度上缩短网络的训练时间，本文选择训练一种前馈网络来用于风格转换，利用预训练好的VGG 网络参数计算风格损失以及内容损失。转换网络采用深度残差网络，充分利用残差网络容易优化、不易发生梯度消失的特性，优化网络训练过程。前馈网络训练过程不需要通过2 次预训练网络，降低了计算量，并且每经过一定的训练次数，保存网络参数从而能够在训练完一种风格后保存网络参数，在进行风格转换时不需要重新训练网络。

1.2 图像内容与风格表示

本文使用预训练的VGG-19 网络来计算转换后图像的内容损失以及风格损失。当图像经过了VGG-19 网络再重构，从越高层次网络获得重构图像，由于越高层网络将得到图像更深层次的特征，将只保留图像内容与整体空间结构，但纹理、形状、颜色等将无法复原。

图1 根据不同层数据进行图像重构示例Fig. 1 Image reconstruction examples based on data of different layers

为了获得图像风格的特征，本文采用Gatys 所提出的Gram 矩阵来作为计算依据。Gram 矩阵是内积空间的一个由内积组成的对称矩阵，它能够给出不同滤波器之间的相关性。Gram矩阵公式如下，其中i，j为特征图序号，l为网络层数:

通过得到预训练VGG 网络中多个层的特征相关性，可以获得输入风格图像的静态多尺度表示，从而能够捕获其纹理特征，而非全局布置。这样一来，就能可视化进行了风格转换后得到的重构图像与给定的风格图像之间风格特征的信息。图2 给出了VGG 网络的其中2 层对于风格重构的示例，在实验中本文将选取多层的数据作为风格图风格表示的依据，然后通过最小化风格图的Gram 矩阵与生成图的Gram 矩阵之间的均方距离来进行网络的训练，遵循公式如下:

图2 不同层风格重构示例Fig. 2 Different layer style reconstruction examples

最终，在网络的训练过程中，给定一个结合了特征重构损失以及风格损失的损失函数，利用随机梯度下降法最小化损失函数来训练网络，训练过程中不断利用训练中的网络来重建输入风格图从而判断网络的训练程度与转换能力。

1.3 图像纹理特征分析

由于图像的损失函数数据计算来源于预训练网络计算的图像深层Gram 矩阵，Gram 矩阵的本质是图像像素之间的内积对称矩阵，因此风格图以及内容图的像素分布将会影响相应的风格转换效果。为了找到其中的规律以及优劣性，本文提出将图像的纹理特征，如信息熵、各阶矩特征来分析网络对于不同输入图像输出的优劣性以及如何选取合适的风格图与内容图来进行转换，从而得到更好的效果。

熵是一个体系中混乱程度的表达形式，在信息论中，熵代表的是概念空间中所携带的信息量的总和，因此又被称为“信息熵”。由于信息熵能够表示信息量的大小，因此在图像处理中，图像的信息熵能够表示一幅图像所携带信息量的大小，在图像的分割与识别起到了巨大的作用。图像信息熵的计算公式为:

其中Pi表示的是某个灰度在该图像中出现的概率，由灰度直方图获得。熵越高那么图像越复杂，图像的灰度中就包含了更多的数据量，也就能够携带更多的内容及风格特征。

随机过程中的矩是对变量分布和形态特点的一种度量方式。在图像识别领域，矩被广泛用于特征提取并取得了良好的效果。利用图像不变矩来提取图像特征具有简单，并且不受噪声、几何形变等干扰的优点，是图像特征的一个良好刻画。图像不变矩的计算公式为:

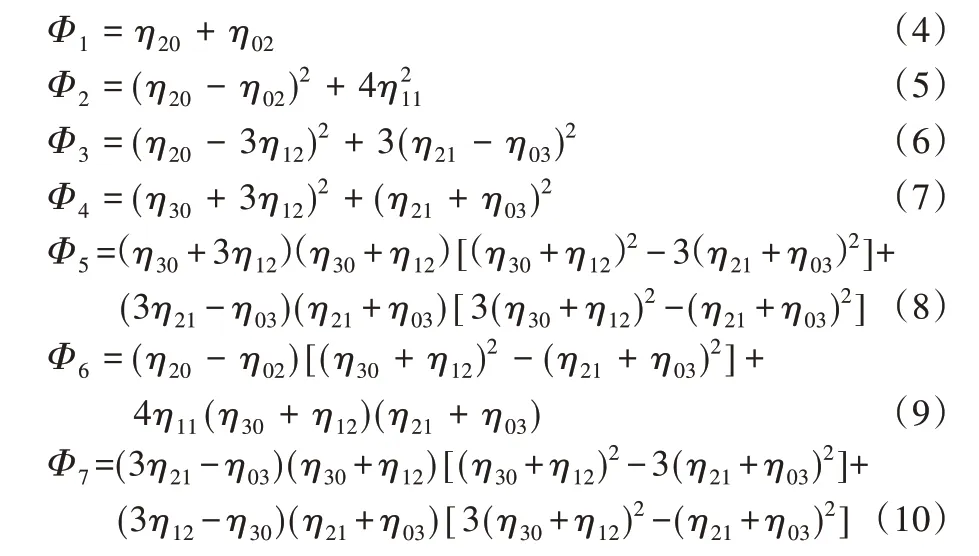
利用图像的信息熵与不变矩对于图像特征的良好刻画，可以更好地理解在图像风格转换过程中，不同的风格图与内容图的特征对于网络的转换效果的影响，从而找到改善效果的方法。

2 结合图像纹理特征的风格转换算法

2.1 算法分析

本文提出一种前馈深度残差网络来进行图像的风格转换。在图像的风格损失方面，Gatys 所提出的Gram 矩阵对于图像的色彩以及纹理十分敏感，能取得较好的效果，如1.2 节所述，因此本文也使用输入图像的Gram 矩阵信息来作为风格损失函数依据。在结构上，本文在Johnson、Gatys 等算法的启发下，采用深度网络前馈网络作为网络的整体结构，而网络的权重依据则来自于预训练的VGG-19 网络。网络选择方面，考虑到Gatys等算法所使用的卷积神经网络在层数增加时，容易出现梯度消失与梯度爆炸，并且计算量十分庞大，因此本文算法转而使用残差网络作为转换网络的主体，利用残差网络容易收敛，不会出现梯度爆炸与消失的训练优势来进行网络的训练，同时为了增大网络的感受野，前后增加了2 层卷积层来对输入图像进行处理。此外，在实验过程中，发现输入图像的信息熵与矩特征对于网络的转换效果有影响，将输入网络的纹理特征分析加入到算法中，达到针对不同输入图像采用相应的处理来提升效果的目的。

网络主体由7 层残差层组成，残差层之前使用一层步长为2的卷积层进行下采样，之后使用步长为1/2的反卷积层进行上采样将图像的大小还原。由于在每一个卷积层后都使用了标准化和ReLU激活函数，因此在最后使用tanh函数来将输出值控制在［0，255］区间。

标准优化算法训练的网络，随着网络层数加深，网络的效果却并不一定越来越好，网络的训练错误往往会呈现先减少后增加的状态，并且容易出现梯度爆炸或者消失的情况。残差网络的特殊结构使得在数据传输的过程中，有很多的旁路将数据直接传输到了后面的层，在学习过程中只学习输入与输出的差值，从而一定程度上解决了梯度爆炸或消失的问题并且简化了计算，降低了学习难度。另一方面，残差网络在学习恒等函数（Identify function）上有良好的表现，由于图像风格转换过程中，应当尽量使得输入图像与输出图像共享图像结构，因此残差网络这一特性也能够运用到风格转换的研究。

在残差网络前后使用卷积层与反卷积层，主要目的是在加深网络的同时，减少计算量并增大有效感受野。为了能够高质量地进行图像的风格转换，应当在不改变原图内容的条件下尽量连贯地改变图像。因此对于每一个输出像素，在输入中如果有对应有效且更大的感受野将能够提高转换效果。所以利用卷积层进行下采样与上采样等手段增加感受野大小，可以提升残差网络对于图像的转换效果。

2.2 损失函数

为了能够衡量输出图像与输入图像的差异性，本文定义了图像重构损失（即内容损失）与风格损失两个函数来进行训练。如1.2 节中所述，本文的损失函数数据来源于预训练的网络，因此这些感受损失函数本身就来源于深度网络，携带着图像的深层特征。

本文不再简单地将输入与输出每个像素进行对比来判别输入图像与输出图像在图像内容上的区别，这样难以在图像的内容上与风格上达成平衡。定义预训练的深度网络为φ，那么φj(x)表示该网络对于输入图像第j层的激活输出。由于j是深度网络的第j层，因此φj(x)就是一个维度为Cj*Lj*Wj的特征图（C为卷积核个数，L*W为特征图大小），那么图像重构损失就可以表示为:

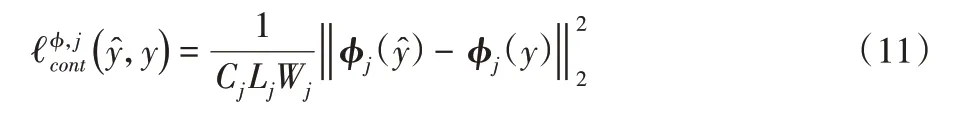
当从预训练网络的高层进行图像重构时，只有图像的整体空间结构得到保留，形状、纹理、颜色等则不然。因此本文使用预训练网络的多个低层数据作为损失函数依据来进行网络训练。

对于风格损失，如1.2 节中所述，为了使得输出图像的风格能够保留风格图的色彩、纹理、模式等，本文使用Gram 矩阵来作为图像风格的表示。如上述φj(x)表示该网络对于输入图像第j层的激活输出，那么定义该层的Gram矩阵为:

φj(x)给出了第j 层图像每个网格的特征，Gram 矩阵则是将图像的每个网格视作独立的样本，以协方差矩阵的形式求出了不同网格之间的关系，而这个协方差矩阵中隐含了图像的纹理、模式等信息，因此可以利用Gram 矩阵作为图像风格损失函数的依据。那么图像风格损失函数为:

本文的网络结构主旨就是利用预训练网络低层数据作为图像重构损失的依据，利用多个不同层的Gram 矩阵作为图像风格损失依据，最后给予两种损失函数相应的权重并进行组合得到总损失函数。

2.3 结合图像纹理特征分析

针对不同的风格图与内容图，分别计算它们的信息熵与各阶不变矩，从而探究输入图像的纹理特征对于风格转换效果的影响。风格图与内容图的信息熵如表1所示。

表1 不同风格图与内容图的信息熵Tab. 1 Information entropies of different style images and content images

风格图与内容图的常用不变矩特征如表2和表3所示。

表2 不同风格图的各阶矩Tab. 2 Different order moments of different style images

图3（a）中4 幅图作为图像风格转换研究中的风格图，属于绘画风格。其中Style-1、Style-2、Style-3 属于西方风格画，Style-4是中国传统山水画。而图3（b）作为图像风格转换研究中的内容图，其中Con-1 是中国传统山水画，另外的6 幅均为相机拍摄图片，其中Con-2、Con-3、Con-4、Con-5 是风景相片，Con-6与Con-7是人与马的相片。

本文发现，Style-1 与Style-2 的信息熵相对于其他两张风格图更大，包含更多的信息量，但风格图都是绘画，因此整体性很强，矩特征差距不大。而内容图中，只有Con-7 信息熵较小，但发现Cont-3、Cont-4、Cont-7的高阶不变矩相对更大。

对于信息熵较低的风格图，图像的像素之间呈现出更低的相关性，而Gram 矩阵是根据图像中各个像素点之间的内积而组成的，在训练时网络会更加难以捕捉到风格图更深层、更细致的特征，因此需要增大网络对于风格的敏感性。本文在训练网络时，风格损失的权值选择为200，内容损失选择为15。对于信息熵低的风格图，将风格损失的权值增加到250，并且在训练过程中增加高斯噪声，所得收敛效果如图4。

图3 用于图像纹理分析的输入图像Fig. 3 Input images for image texture analysis

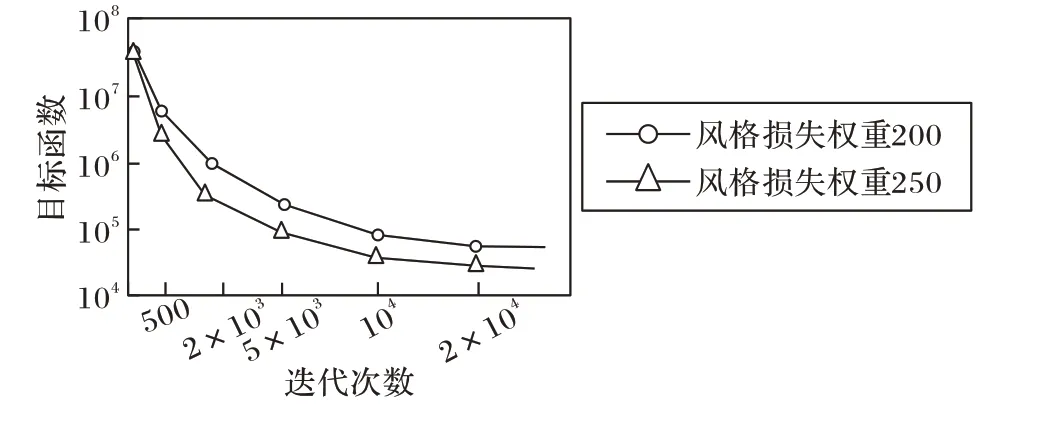
图4 改变权重训练收敛对比Fig. 4 Training convergence comparison of changing weights

从训练收敛速度来看，当风格损失权重增大时，网络的收敛速度会加快，因此学习过程更不容易产生过拟合，对于内容图的结构学习能力下降，但对于风格的敏感度提升，能够使得输出更好的带有风格图的风特征，对于信息熵低的风格图也能有良好的效果。

在此基础上，本文在50 幅风格图的基础上进行了更多研究，最终根据结果分析，确定一个信息熵阈值δ，当它低于7时，将风格损失的权重增大到250，低于6.5时，增大到300。

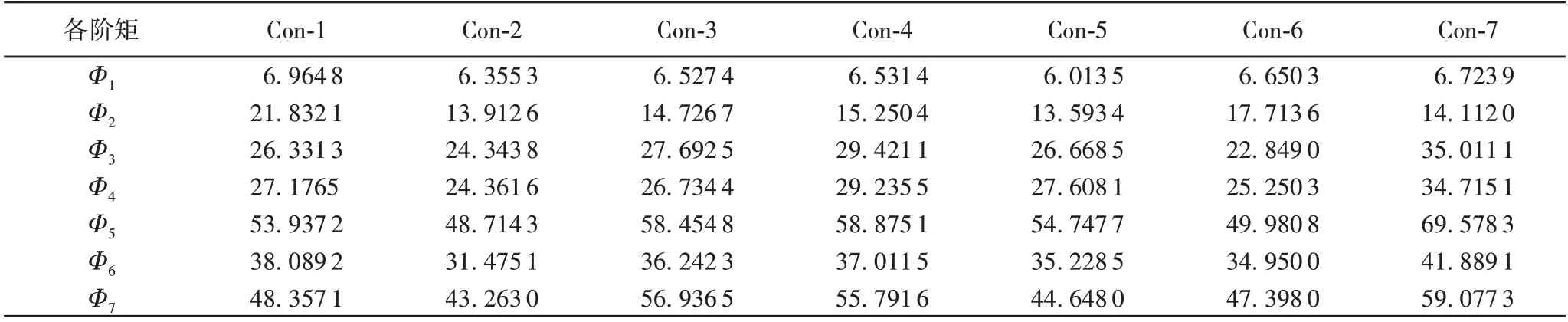
表3 不同内容图的各阶矩Tab. 3 Different order moments of different content images

对于高阶矩大的内容图，容易出现一些空白的部分，网络往往能够良好地转换内容图的主体部分，对于内容图中的空白部分无法良好地赋予与风格图相应部分类似的纹理。因此，根据对高阶矩的分析，网络对于高阶矩更低的内容图有更佳的转换效果，对高阶矩高的内容图的转换效果则相对差一些，因此在图像风格转换过程中，高阶矩低的、背景完整的内容图能够得到相对更好的效果，这一规律对于如何更有效地利用图像风格转换网络具有指导意义。

2.4 总体转换模型

网络的整体结构如图5，对于输入图像，基于图像纹理分析，发现输入图像的信息熵与矩特征对于转换效果的影响规律，并据此调整网络训练参数以及采取合适的处理方法来提升转换效果。主体结构使用残差网络作为图像转换网络，结合下采样层和上采样层来增大网络的感受野，提升转换效果。损失函数利用ImageNet 上预训练的VGG-19 作为损失网络，使用图像重构损失作为图像的内容损失，输入图像与输出图像Gram 矩阵的欧氏距离作为图像的风格损失，将两种损失函数加权得到总损失函数，作为网络训练的依据。

3 实验分析与结论

3.1 实验数据与模型参数

本文利用COCO2017 年的图像数据集作为训练数据（图6），将每个训练图像的大小调整为256×256，批量为2，进行80 000次迭代。本文使用Adam 作为优化方法，将学习率设置为10-3，学习率衰变设置为10-5，将预训练网络的Relu4_2层数据用来将计算图像重构损失，Relu1_1、Relu2_1、Relu3_1、Relu4_1、Relu5_1 层的数据用来计算风格损失，每训练200 步保存网络数据，每600 步进行网络验证，用于检验当前网络的转换能力。训练过程在单个GTX1080ti的GPU 上训练大约需要5 h。

从图7 可以看出，随着迭代次数逐渐增加，网络对于图像风格的掌握程度逐渐提高，从早期只能识别图像的整体结构到既能够保留色彩、结构，也能保持图像的内容。

图7 不同迭代步数的验证图Fig. 7 Verification diagrams with different iteration steps

3.2 实验结果分析

3.2.1 基于风格图分析

从图8 的三种转换效果可以看出，由Style-1 与Style-2 作为风格图所训练的网络，根据2.3 节的计算结果，风格图的信息熵高，呈现出的转换效果非常好，能够在保持内容图内容保持一致的条件下，将风格图的风格赋予在输出图像中，并且带有明显的风格图的纹理特征。而以Style-3 作为风格图时，由于风格图的信息熵相对低，图像对于天空部分把握不佳，主体建筑物周围的天空呈现出与建筑物相同的风格，与右上角部分有较大区别，但转换后图像对于内容图有很好的保留。

图8 三种风格图的转换结果Fig. 8 Transfer results of three kinds of style images

在以上基于图像纹理特征分析的基础上，尝试增大训练过程中风格损失所占比重，将风格损失与内容损失比重从200∶15 增大到250∶15，并在转换后期添加了高斯噪声处理来使得天空部分更加均衡，重新训练后得到如图9所示结果。

图9 优化前后结果对比Fig. 9 Result comparison before and after optimization

从图9 可以看出，在进行了网络优化后，输出结果相对更好，塔顶部分周围的天空从一开始出现不规则的黄色区域，优化到整个天空的风格趋于一致，并且建筑物方面的风格也更加统一。图10给出了更多的优化结果。

3.2.2 基于内容图分析

从图11 与图12 的结果来看，图11 中的内容图高阶矩更高，网络对于图像的主体部分转换效果良好，但是对于背景的部分则效果不佳。而图12 中第一幅图马的转换不仅马本身，背景也成功转换为风格图的风格；第二幅图不仅山的主体部分转换效果好，左上角的天空部分没有多余的不规则纹理，呈现出与风格图相同的空白，效果明显优于图11 中的（b）。在此基础上进行了更多的实验，图像风格转换网络对于高阶矩更低的风格图有更佳的转换效果。

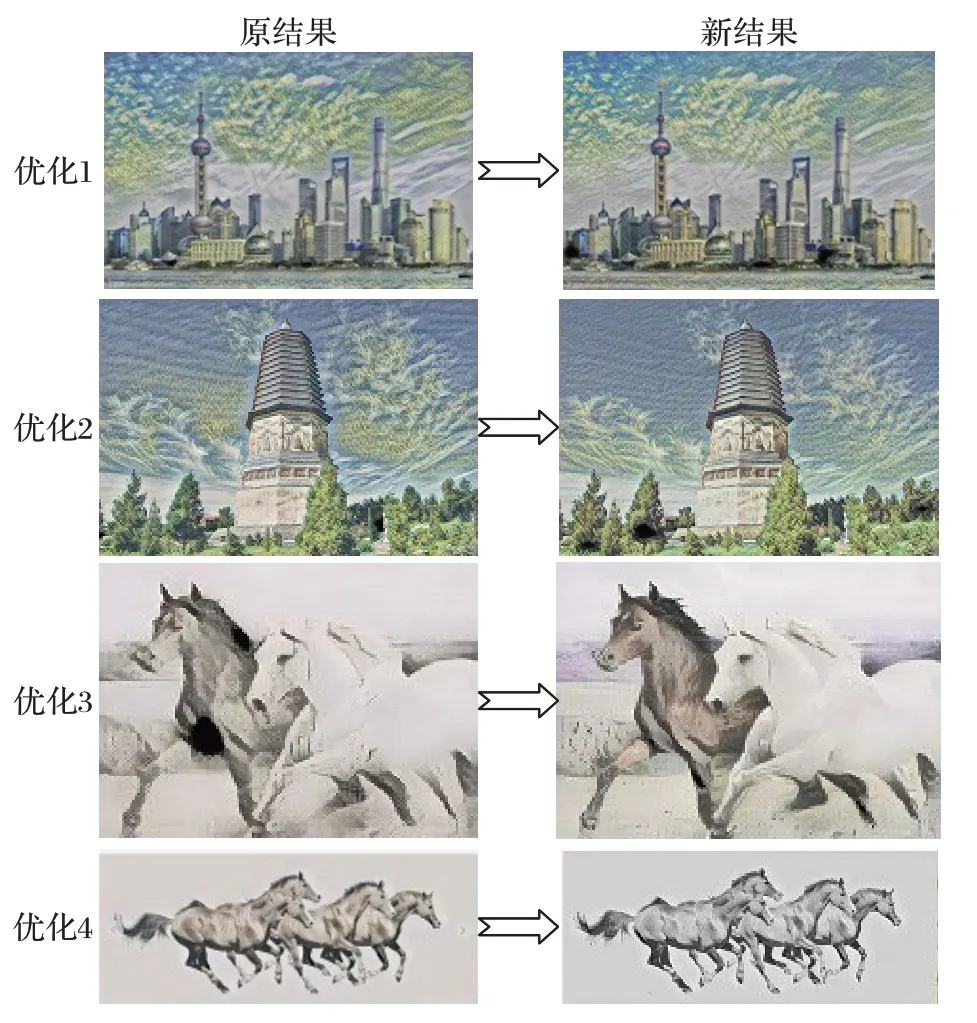
图10 更多优化结果Fig. 10 More optimization results

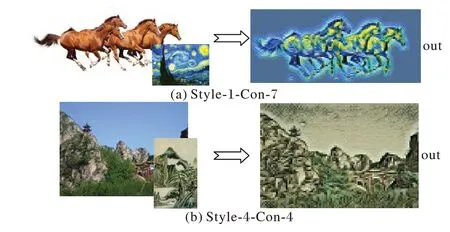
图11 针对内容图分析的结果Fig. 11 Results of content image analysis

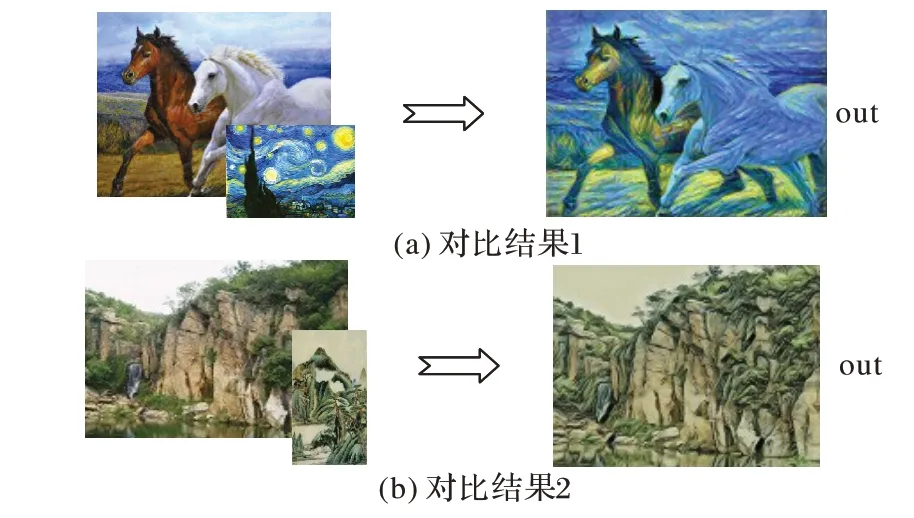
图12 高阶矩更低内容图的效果Fig. 12 Results of content images with lower high-order moments

3.2.3 基于图像纹理特征分析总结

综上所述，在图像的转换过程中，风格图的信息熵越大，网络就能够更好地把握风格的纹理特征，输出图像的整体性更佳。另一方面，内容图的高阶矩越大，那么由Gram 矩阵所计算出的风格损失所占比重就会增加，使得输出更注重于保留内容图的整体结构特征，而对于风格的转换效果不如低高阶矩的图像。通过实验分析，风格图的信息熵偏低时，通过增大训练时风格损失的比重，来提升网络对于风格的敏感度，并且利用高斯噪声等图像处理方法，能够提升转换效果；另一方面，在风格图与网络固定时，网络对于高阶矩更低的内容图有更好的转换效果，这对于如何更有效利用网络具有指导意义。

3.3 与其他网络对比验证

除了对比不同风格图以及内容图的结果，本文还将本文网络与提出Gram 矩阵的Gatys所提出的图像风格转换的卷积神经网络以及Stylebank进行了对比，结果如图13所示。

图13 本文网络与Gatys网络和Stylebank网络的对比Fig. 13 Comparisons of the proposed network with Gatys network and Stylebank network

通过图13 可以发现:与Gatys 网络对比，得到了更加明亮、更加细腻的结果，整体的风格也与风格图更加契合，除了风格纹理之外，网络对于亮度、色彩等方面把握更加优秀；而与Stylebank 相比，由于风格图是来自于毕加索的一张抽象的人像，将内容图中整个人转换成该风格较为困难，Stylebank的结果除了有一个人的大致轮廓外，与原图差距过大，而本文的结果大致保留了原图的所有内容特征，人物轮廓、背景的广告板等都有较高的识别度，在纹理方面，做到了和风格图类似的不同区域分隔明显的特征，整体效果优于Stylebank网络。

表4 用3 中风格图作为例子，对比了3 种网络的训练耗时。表5 对比了3 种网络的转换耗时，在输入3 种不同尺寸的图像上进行了对比。由于Stylebank 网络无法保存已训练数据，因此训练耗时即转换耗时，每转换一张图片都需要重新训练网络，较为不便。与Gatys 的网络对比，本文网络的训练耗时以及转换耗时都更短，在效率上远优于Gatys网络。

由于三种网络采用的方法不尽相同，为了能够更加直观地看出不同网络对于风格转换的效果，将不同网络的输出结果图利用Gram 矩阵计算的风格损失进行了统计。由于对于不同风格图，输出的风格损失差别较大，因此以Stylebank 网络作为基准进行归一化后，进行风格损失的对比，结果如表6所示。

表6 风格损失对比Tab. 6 Comparison of style loss

表6 表明，在输入的风格图相同时，本文网络计算所得的归一化风格损失更小，因此在风格上，本文的结果更加接近于原图的风格特点，在风格转换方面的效果更佳。

4 结语

本文提出了一种结合图像纹理特征分析的前馈图像风格转换网络算法，通过训练具有感知损失函数的前馈残差网络网络来进行风格转换，利用输入图像的信息熵和不变矩特征分析，发现了输入图像的特征与输出效果之间的关系，从而实现了对网络的针对性改善。大量实验结果表明本文所提出的算法在提升了图像风格转换效果的同时，大大提高了转换效率。下一步的研究方向是提取图像更多更深层次的特征来进一步分析各种特征对于网络转换效果的影响，并在更多不同种类的图像上进行实验，使分析结果更具有鲁棒性和全面性。