基于适应度函数的无人船遗传算法航径规划

刘长吉，黄宴委

(福州大学 电气工程与自动化学院，福州 350116)

0 引言

近年来，无人船得到越来越多的关注，其中路径规划是无人船研究领域的关键问题之一。路径规划旨在从障碍物环境中，找到一条从起始位置到目标位置的无碰撞可行路径。关于路径规划的研究有很多，使用了各种方法。每种方法在不同的环境中，都有其优缺点。遗传算法最初是由Holland提出的[1]，被认为是一种启发式的，鲁棒性强的优化技术，在大多数优化问题中都能取得较好的效果[2]。Yao Z等人将遗传算法应用于静态环境下移动机器人的路径规划问题中[3]，提出一个算术适应度函数和两个自定义遗传算子，结果表明该方法在简单的环境中能够较快获得最优解，但在复杂的环境中难以获得最优解。Zhang X等人提出一种改进的遗传算法[4]，该方法利用可见空间的概念获取初始种群，并提出两种新的变异方法保证算法收敛到全局最优解，虽然该方法在复杂环境下能获得最优解，但是计算过于复杂。Tuncer等人提出一种新的变异算子[5]，该方法从离突变节点较近的所有自由节点集合中随机选取一个节点，然后根据适应度函数值选取突变节点，与其他方法相比，该方法的收敛速度较快效果较好。然而上述路径规划方法所生成的路径都是由线段组成的，并不是光滑的路径，这将迫使无人船在转折角处停止，转弯，重新启动才能沿着规划好的路径航行[6]。因此必须使路径变得光滑。近十年来，贝塞尔曲线在光滑路径规划问题中得到越来越多的应用[7-9]。Baoye等人提出一种新的移动机器人平滑路径规划遗传算法[9]，该方法用于寻找最优控制点，确定基于贝塞尔曲线的光滑路径。值得注意的是，这些方法着重于对遗传算子的改进和路径光滑程度处理，而未考虑到实际机器人的机动性能。由于无人船是一个高度欠驱动的系统[10]，因此在无人船航径规划中必须考虑无人船的机动性能。

本文提出一种基于适应度函数的无人船遗传算法航径规划方法。在初始种群中，以染色体的路径点作为贝塞尔曲线的控制点，利用贝塞尔曲线优化方法，将初始的折线路径变成光滑的曲线路径；在路径选择中，以无人船最小转弯半径为约束条件，设置路径的最大曲率，在适应度函数中添加曲率判断，利用适应度函数选择出符合约束条件的曲线路径。在仿真实验中，采用基于网格图的方法构建规划环境，验证所提出方法的有效性。

1 贝塞尔曲线改进遗传算法

本节在遗传算法的初始种群中利用贝塞尔曲线，对初始种群生成的折线路径进行平滑优化，在适应度函数中添加曲率判断，以最小转弯半径为约束条件设置曲线曲率，利用适应度函数筛选出符合最小转弯半径约束的曲线路径。改进的遗传算法路径规划流程图如图1所示。

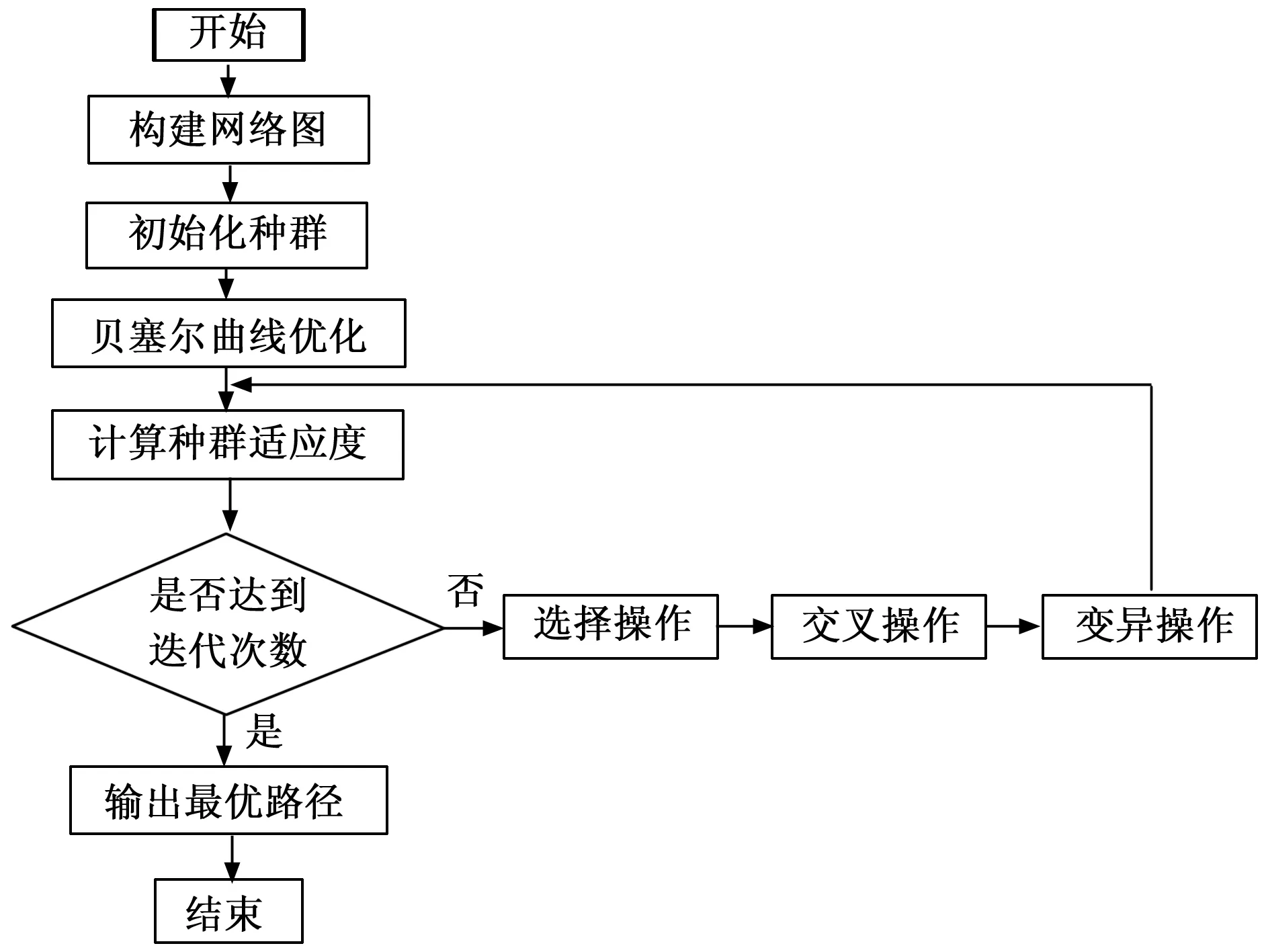
图1 改进遗传算法路径规划流程图

将改进遗传算法应用在路径规划问题中，主要分为以下几个步骤：首先，先构建路径规划所需要的规划空间；然后根据染色体的编码方式生成初始种群；紧接着将生成的初始种群中的染色体经过贝塞尔曲线优化；然后根据适应度函数计算初始种群中染色体的适应度值，并根据染色体适应度值的大小对染色体进行选择；将选择出的染色体经过交叉和变异操作，以产生出适应度值更佳的染色体，最后经过不断迭代，当迭代次数到达预期的次数时，则停止迭代根据适应度函数值筛选出最终的最优路径。

1.1 规划空间表示

规划空间指的是无人船路径规划所需要的环境区域，包含障碍物区域和无障碍物区域。现有的路径规划方法大都使用网格图的方法来表示规划空间[4-5,11-12]。如图2所示，白色网格表示自由区域，灰色网格表示障碍物区域。本文采用矩阵编码的方法来表示网格位置[4]，网格的位置由行索引和列索引决定。例如，b1,3表示第一行第三列的网格位置。

图2 规划空间示例

1.2 染色体编码和初始种群

染色体表示在路径规划问题中生成的候选路径。染色体是由起始节点，目标节点和无人船航行过程中所经过的节点组成。这些节点通常被称为染色体的基因。常用的染色体编码方法主要有二进制编码，浮点数编码，十进制编码和字符编码。本文使用文献[4]中的编码方法来表示染色体，该方法对字符编码进行了一些改进，使其不需要解码，并且能更直观的表示各个节点的位置信息，如图3所示。

图3 染色体示例

传统遗传算法中初始种群的生成方式一般采用随机生成的方法，即随机生成一系列染色体。但在路径规划中，这些随机生成的染色体可能包含一些不可行的路径，导致这些路径与障碍物相交。虽然通过遗传算子不断迭代的过程最终也能找到最优解或接近最优解。但这一迭代过程降低了算法的搜索速度，并增加了算法的计算时间。为了解决这个问题，将从自由区域中随机选择染色体的节点。首先在染色体生成之前先获取障碍物区域，由于规划空间采用矩阵编码的方法表示，可以快速获取障碍物的形状和位置。然后从障碍物区域以外的自由区域中随机选择节点生成初始路径。如图3表示初始种群中的一条染色体，其中b1,1表示起始位置，b6,6表示目标位置，b4,1，b4,4和b6,4表示所经过的路径点。

1.3 基于贝塞尔曲线的初始种群生成方法

由于遗传算法生成的路径是折线路径，并不是光滑的曲线路径，如图4所示。如果无人船沿着规划好的折线路径航行时，必须在每个转弯点停下来调整航向角再重新加速航行，这一过程既占用时间又损耗机器性能。因此，必须把折线路径变成光滑的曲线路径，使无人船无需停止调整航向角就能够沿着规划好的路径航行。本文采用贝塞尔曲线来改进初始种群平滑优化，贝塞尔曲线是通过线性插值的方法来实现的，它能简洁完美的表达自由曲线和曲面，在计算机图形学中得到了广泛的应用。因此，贝塞尔曲线是一种很好的曲线拟合工具。下面将介绍贝塞尔曲线实现的主要方法，首先将初始种群中染色体的n个路径点当做贝塞尔曲线的控制点p(j)，j=0,1,2,…,n。如p(j)=(b1,1,b4,1,b4,4,b6,4,b6,6)是初始种群中的一条染色体，p(0)表示染色体中的第一个路径点b1,1。贝塞尔曲线由这些路径点定义如下：

(1)

其中:t是归一化时间变量，p(j)=(xj,yj)T表示染色体中第j个路径点的坐标向量，xj和yj分别对应x坐标和y坐标的分量，Bj,n(t)是伯恩斯坦基多项式表示贝塞尔曲线中的基函数，定义如下：

j=0,1,2,...,n

(2)

优化后的路径如图3实线路径所示。贝塞尔曲线的导数也是由这些路径点确定的，贝塞尔曲线的一阶导数如下所示：

(3)

贝塞尔曲线的高阶导数也可以通过计算得到。例如，贝塞尔曲线的二阶导数表示为：

P″(t)=

(4)

在二维空间中，贝塞尔曲线关于t的曲率表示为：

(5)

图4 初始路径示例

1.4 适应度函数曲率优化

无人船路径规划问题的目的是从起始位置到目标位置之间找到一条最优的无碰撞路径。遗传算法是通过适应度函数来选择路径的，所以在适应度函数中必须考虑路径的平滑性和可行性。因此适应度函数的选取至关重要，本文的一个关键概念是在适应度函数中考虑无人船的机动能力。由于无人船的转弯半径是有限的，为了保证路径可行，只需对路径的曲率进行约束[13]，无人船可行驶路径的最大曲率可以表示为：

(6)

其中:Rmin是无人船的最小转弯半径。以此为约束条件，从优化后的贝塞尔曲线路径中筛选出符合最大曲率约束的路径。遗传算法是通过适应度函数来选择路径的。因此，必须在适应度函数中添加曲率判断，定义如下：

(7)

d[p(j),p(j+1)]=

(8)

其中:f是适应度函数，p(j)是染色体上的第j个路径点，d是两个节点之间的距离，xj和yj表示无人船当前的水平和垂直位置，x( j+1)和y( j+1)表示无人船下一个路径点的水平和垂直位置，k(t)是贝塞尔曲线的曲率计算公式，penalty是惩罚值。适应度函数定义为路径中每个路径点之间的距离和路径的曲率之和。如果路径与障碍物相交，则在适应度函数中加上一个惩罚值；如果路径的曲率k(t)大于最大曲率kmax，则在适应度函数上加上一个惩罚值，惩罚值必须大于工作环境中的最大路径长度。最后通过适应度值的选取来筛选出符合曲率约束的路径，适应度值越小越好。

1.5 选择算子和交叉算子

选择算子的主要目的是通过适应度函数值将初始种群中适应度值较好的染色体保存下来，并移交给下一代。染色体的选择过程主要分为三个步骤：第一步通过适应度函数计算所有染色体的适应度函数值；第二步将计算出的适应度函数值按从小到大的顺序进行排序，并与各自对应的染色体进行配对；第三步是根据适应度函数值选择适应度值较小的染色体放入交配池中以产生新的染色体。交配池中包含两个算子，一个是交叉算子，一个是变异算子。下面先介绍交叉算子，交叉算子的目的是交换染色体间的基因以产生新的染色体，避免陷入局部最优解。本文采用单点交叉算子，从交配池中随机选择两个染色体当父代染色体，在父代中随机选择一个节点作为交叉点，将交叉点后的两个父代染色体的基因相互交换。换句话说就是，第一个子代染色体是由第一个父代交叉点前的基因和第二个父代交叉点后的基因构成的。第二个子代染色体是由第二个父代交叉点前的基因和第一个父代交叉点后的基因构成的。交叉过程如图5所示。

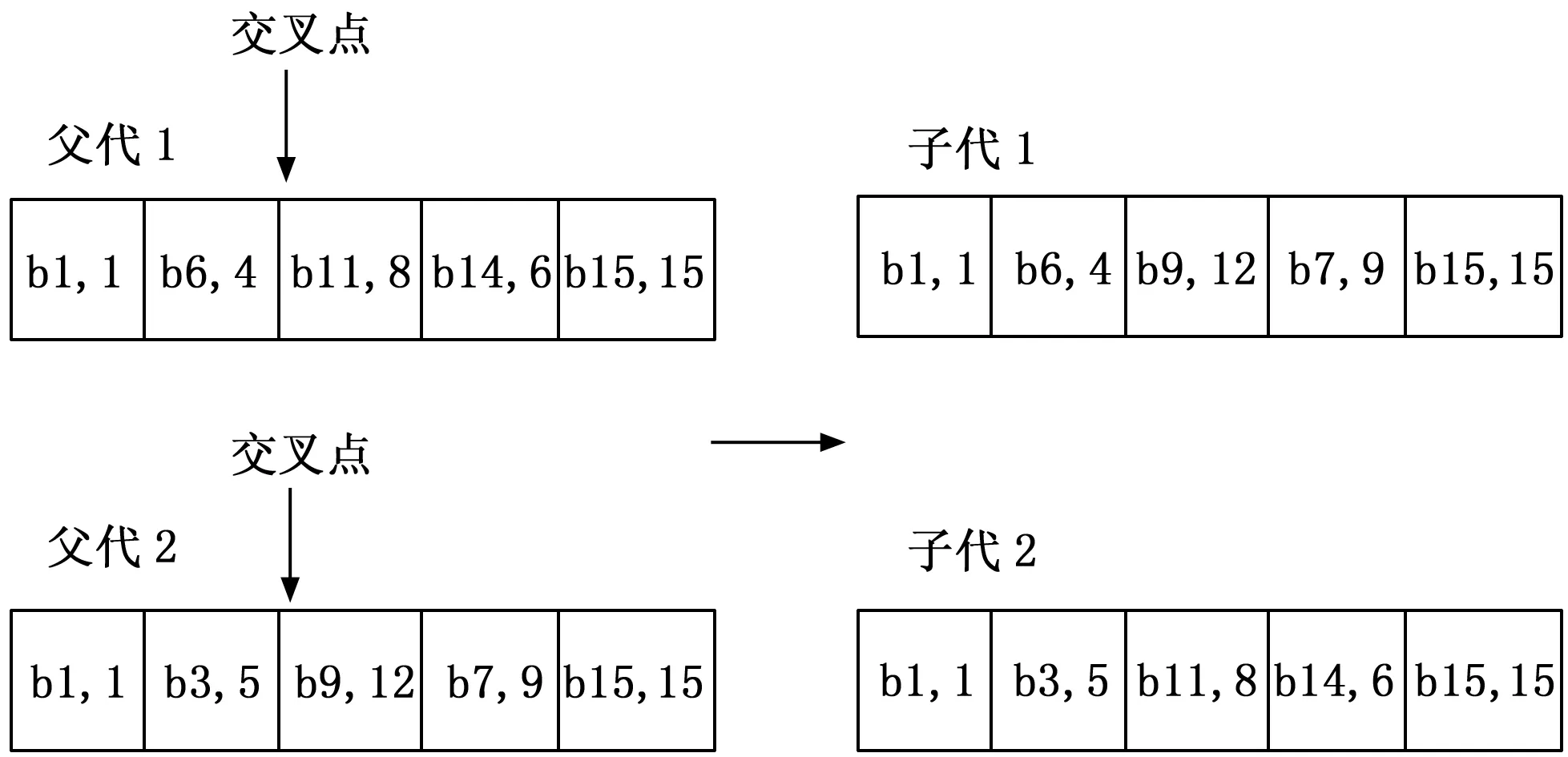
图5 交叉过程

1.6 变异算子

变异算子的目的是增加种群的多样性，避免过早收敛的现象。本文的变异算子是基于文献[5]中提出的。在现有的文献研究中[3,11-12,14]，该算子具有较好的效果。该方法首先从突变的染色体中随机选择一个不是起始或目标节点的节点作为突变节点。然后，定义一个集合，该集合由突变节点的所有可行邻居点组成，由于采用矩阵编码，可以很快获得突变节点的邻居集合。再依次从邻居集合中选取一个节点代替突变节点，并计算所有路径的适应度值。最后，选择适应度值最小的路径节点替换原始突变节点。

2 仿真实验与分析

本实验使用Python编程实现，并运行在一台Intel Core i7处理器和8 GB内存的计算机上。为了验证该方法的有效性，将其应用于16×16的网格图中，并与文献[9]的方法进行比较，其中包含12个障碍物区域，起始点位置为(1,1)，目标点位置为(15,15)。主要参数如下：无人船最小转弯半径Rmin=0.2 m，则最大曲率kmax=5 m-1，在[0,1]区间构造具有80个样本数的等差数列作为伯恩斯坦基多项式t的值，种群大小取80，最大迭代次数取100，交叉概率为1，变异概率为0.3，对于每个不可行路径的罚值取100。如图6为遗传算法、平滑算法和本文方法在相同环境下形成的路径比较。从图中可以看出遗传算法生成的路径是折线路径，并不适合无人船航行。平滑算法只对路径进行平滑优化，并未添加曲率约束。使用本文方法生成的路径更为平滑，曲率更小。图7为平滑算法和本文方法生成路径的曲率比较，从图中可以看出平滑算法生成的路径曲率过大，并不能满足无人船最大曲率约束的曲线曲率，而本文算法生成路径的曲率明显小于最大曲率约束，因此可以得出本文方法生成的曲线路径是符合无人船最小转弯半径约束的。图8给出了平滑算法和本文方法每代最优染色体的适应度函数值，可以看出本文方法的收敛性更快。表1为平滑算法和本文方法的性能指标对比，性能指标有3个：(1)最大曲率，用来评估路径是否符合无人船最小转弯半径约束，该值小于5表示路径符合无人船最小转弯半径约束；(2)平均适应度函数值，该值是路径长度和曲率之和，该值越小表示路径越短。(3)平均搜索时间，用来评估算法的时间性能，该值越小表示算法搜索时间越快。从表中看出本文方法生成的路径符合无人船最小转弯半径约束，平均适应度值和平均搜索时间均优于平滑算法，说明本文方法性能更好。

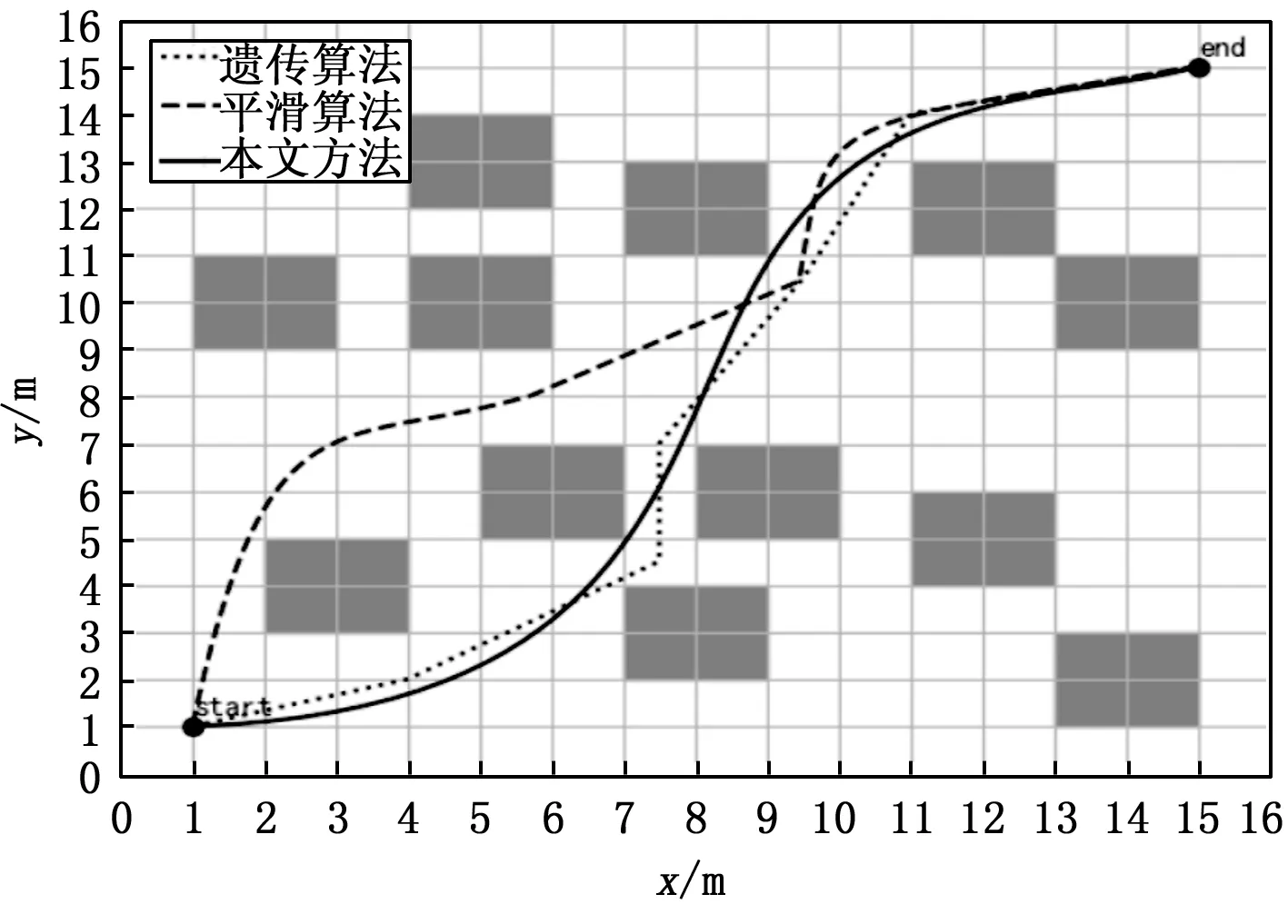
图6 路径效果对比

图7 路径曲率比较

图8 适应度函数值比较

表1 平滑算法与本文算法的性能比较

最大曲率(1/m)平均适应度值平均搜索时间/s平滑算法16.6360.710.76本文方法0.3052.350.59

3 结束语

本文提出一种基于适应度函数的无人船遗传算法航径规划方法，为了使遗传算法生成的折线路径变成曲线路径，在遗传算法初始种群中结合贝塞尔曲线优化方法。在算法中考虑无人船机动性能对航迹的约束，以最小转弯半径为约束条件设置最大曲率，利用适应度函数筛选出符合无人船最小转弯半径约束的曲线路径。通过仿真实验结果验证了该方法生成的路径能满足无人船最小转弯半径的约束，更有利于无人船跟踪航行。