知其然知其所以然知其所以必然
朱锦云

工作将近二十年,一直是大循环教学,总觉得自己对于小学数学知识已然了熟于胸。可读完郜舒竹先生的《小学数学这样教》之后,我开始陷入沉思。知其然,更应知其所以然,知其所以必然。这本书讲述了许许多多被我们所忽略的“所以然”。正如郜先生所说,“所以然”的知识往往具有历史性、贯通性、综合性和人文性,是前人大师长期以来的结晶,是学生难以利用生活经验通过自主或合作的方式探究出来的,是需要教师通过努力学习和研究并潜移默化地传输给学生的。因此,数学教学研究仅限于“如何教”和“如何学”这样的问题是不够的,还应重视“教什么”和“学什么”的研究,特别是对“所以然”知识的研究。
一、“所以然”之一:追根溯源,关注本质
知识感悟:追根溯源是一种刨根究底的学习方法,是探索知识的精神。追根溯源应从小学数学起始型概念知识入手,这是小学数学基础知识的重要组成部分,也是发展学生思维、培养技能的基础,在小学阶段占据重要的地位。作为教师,我们应该弄清楚每一个概念的内涵和外延,以及概念之间的关系,不同的知识采取不一样的方式,让学生“知其所以然”。规律性知识,可以让孩学生经历自主创造的过程,从而感悟到“知识是因需要而产生的”;规定性知识,则通过接收性方式,让学生明白这些规定的历史随机性和规定的合理性,要领会数学课程中“人为规定”的思想性。
比如加法的结果为什么叫做“和”,为什么不是“合”?乘法中的“乘”究竟是什么意思?除法的结果叫做“商”,为什么?“二分之一”究竟是什么意思?为什么叫做“小数”,小数是很小的数吗?“正比例”和“反比例”中的正和反是什么意思?“0”为什么不能做除数?为什么“1”既不是质数也是合数?余数为什么要比除数小?郜教授每一个问题的阐述,每一个思想的提出,都是他对于问题本源的追问。
案例解析:曾经听过本校老师的一节《加法交换律》的课,课堂开始,教师播放动画,动画讲述了“朝三暮四”这个成语故事。孩子们哄堂大笑,几乎秒懂,其实桃子的总个数一样。于是,老师板书“3+4=4+3”,并告知“这就是加法的交换律!”细想一下,这样的结果还是计算出来的。因为3+4=7,4+3=7,所以,3+4=4+3。即只能说明交换两个数的次序后,都等于7。
基于《小学数学这样教》给我的启示,尝试将该环节这样修改:关注“本源”---数数 ,“数,起源于数”。 我们不妨回忆一下,幼儿园时爸爸妈妈是如何教孩子数物体的个数的,就拿 “掰手指”为例,1、2、3、4、5,当5个手指头数结束时,另一只手从第6个数继续开始,6、7、8、9、10,这样就得出有10个手指头的结论。再后来我们学习加法算式时,求一共有多少个?是不是也是引导孩子先将两堆物品合并起来,接着数?想想我们何不在“朝三暮四”这个情景后再加上数数的方法来理解呢?先在3个后面接着数4个,就是7个桃;在4个后面接着数3个,也是7个桃。虽然这个过程看似简单,恰恰从数学的本质上解释了加法交换率。计算得出3+4=7,4+3=7,数数也同样可以,这样添加还可以调动孩子多种感官参与。
当然,后面要学习的《乘法结合律》也可以追溯其本质,用数与算、数与形相结合的方法让孩子体验算理的推导过程,合理的“数学”经历,不仅知道,更知道为什么。数学课程中看似“人为规定”的内容,蕴含着丰富的思想。挖掘这样的规定性内容, 并融入学生数学学习活动中,能让学生感受到数学规定的深刻、丰富、博大与深邃……
二、“所以然”之二:深入分析,提高认识
读书感悟:也许就在某个瞬间,你会推翻自己多年来引以为傲的想法;也许就在某个不经意间,你的思想已经在悄然地生长。在这漫长的“寒假”里,和《小学数学这样教》为伴的日子里,感觉时时刻刻都在不断更新、提高自己的认识。
“用运动的眼光看世界”让我有更多、更深的感触。在此之前,我知道把线看作“点”运动的轨迹,同样运动“线”留下的痕迹成为“面”,立体图形则表现为运动的“面”所留下的痕迹。但从未去深入分析,他们之间还有哪些共性、线段长度、面积大小以及所占空间大小之间的联系。
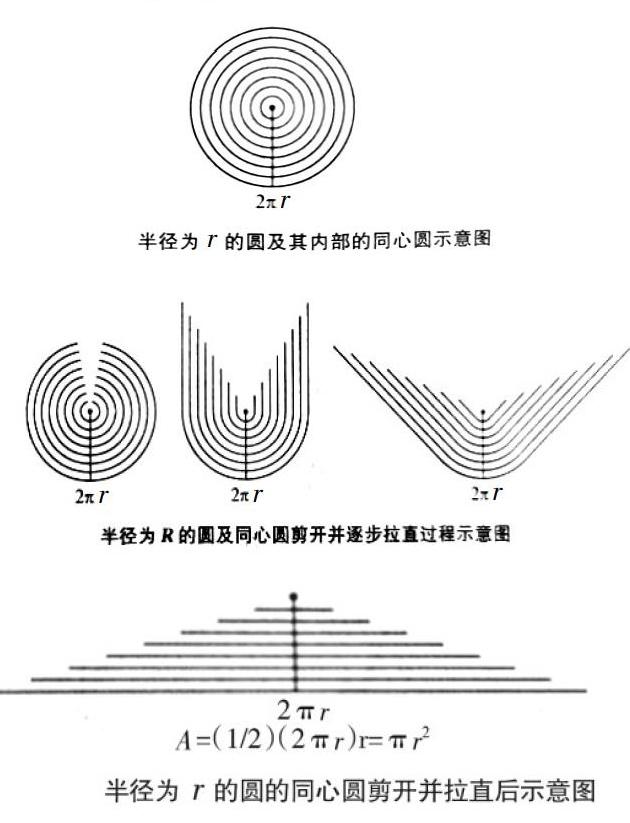
看完第七章后,我知道了:半径为r的圆,圆内部画出许多同心圆。最外围的大圆周长是2πr。想象将圆面从某处剪开,然后逐步展开并拉直,当所有同心圆的圆周都拉直后,就会形成一个三角形。
这个三角形的底边长度就是大圆周长2πr,高就是大圆底面上的半径r,利用三角形面积公式:底×高÷2,得到面积2πr×r÷2=πr2,恰好与圆面积公式一致。
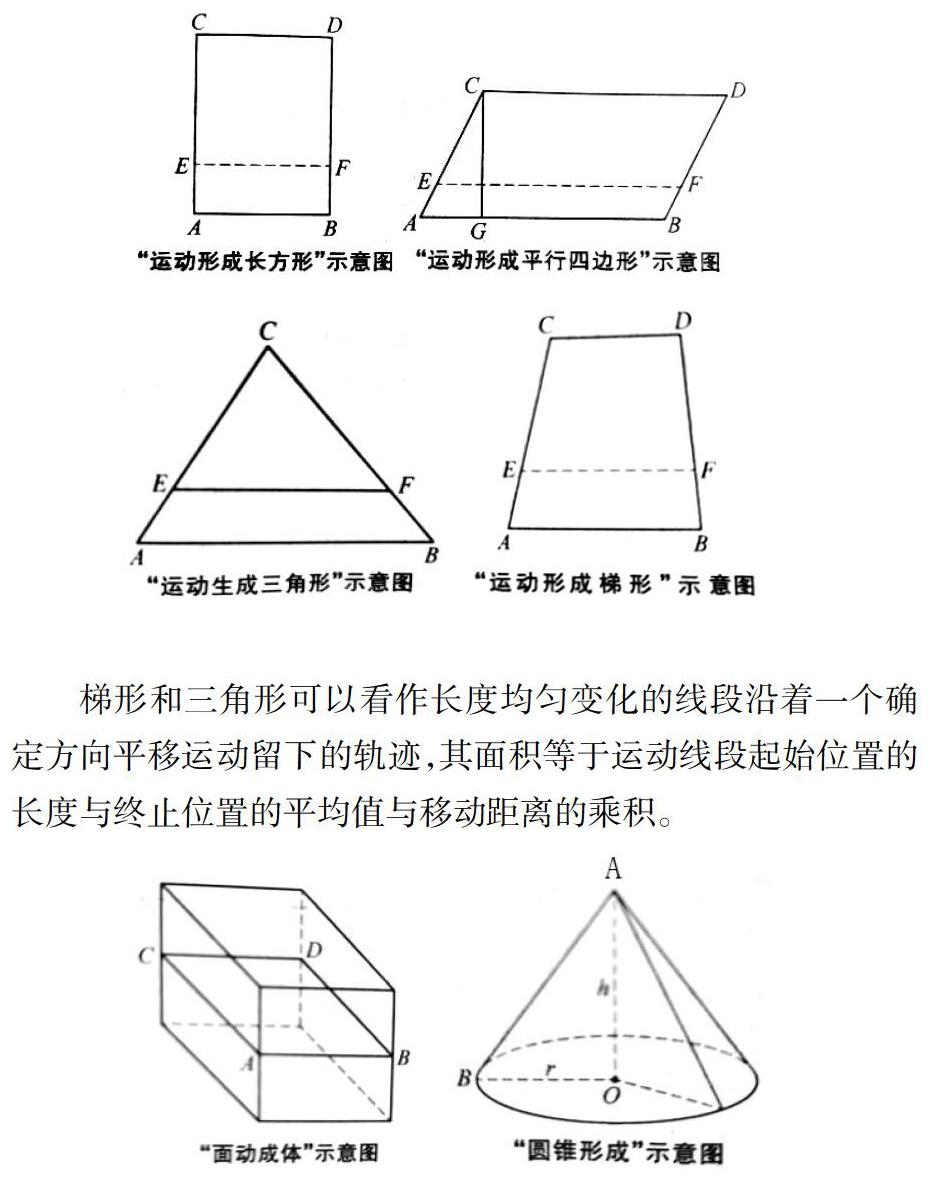
我还知道了:矩形和平行四边形面积都可以看成,通过平移运动在某个方向离开轨迹的直线度留下的轨迹,其面积都是运动线段的长度与运动距离的乘积。
梯形和三角形可以看作长度均匀变化的线段沿着一个确定方向平移运动留下的轨迹,其面积等于运动线段起始位置的长度与终止位置的平均值与移动距离的乘积。
“线动成面”,其面积公式可以认为是“线的长度”与“运动距离”的乘积。那么,“面动成体”体积公式可以认为是“面的大小”与“运动距离”的乘积。很显然,长方体、正方体、圆柱体的体积公式都可以解释。可是,圆锥体积公式又为何是等底等高圆柱体积的三分之一?原来,有时候直观与经验是不可靠的。就如相对论,牛顿的经典物理学在速度不快的地方很适用,但当速度特别快的更广大的宇宙空间,有的公式就不适用。经历这些过程,可能就是课标所提出的让孩子积累基本活动经验,感悟基本数学思想的意思吧。总之,我不仅懂得了微积分的“积分种值定理”,还知道了“旋转体的体积的大小由旋转面的面积和旋转面重心到旋转轴的距离这两个因素决定。”……
疫情结束之后,我们六年级的新课教学也已经结束。那么,复习期间我是不是就可以抓住最初的本源这根线头,带领孩子们一起去讨论、探究知识之间的联系和区别。也许我们所要做的不是去逐个击破,而只要拎紧主线,把孩子放出去,自己找寻、补充知识结构。当他找不到方向的时候,回过头来,发现老师一直在那个源头处等他们,给他们适当的提醒和补充,重新出发,这也许是比较理想的境界。但是我觉得可以。在学习《圆的面积计算》时,我是不是可以将它与三角形的联系图出示,带给他们与我一样的思维和视觉冲击?
不管怎样,我开始反思自己的课堂,反思之前的经验教学的可取与摒弃之处。于是,一种与时下相契合的理念——以学定教、因学施教、变教为学、顺学而导的思想火花掠过我的心头。我们需要转变备课方式、研究方式、教学方式……
三、“所以然”之三:改变课堂,变教为学
读书感悟:当下的课堂,教师追求现有知识的掌握,不大追求让孩子经历知识的发生、发展的过程。教学缺乏一定的“文化性”。只是让孩子接受数学这份“冰冷的美丽”,丧失了知识产生时那“火热的思考”阶段。教学应该让孩子重温人类历史发生发展的重要阶段。因为,人类个体的成长其实在一定程度上反映与重复着人类种族的文明进化过程。
案例解析:六年级下冊《解决问题的策略》第二课中,用假设法解决“鸡兔同笼”。疫情期间,线上教学进行了几周,孩子们的学习劲头开始懈怠。而这部分知识又是教学难点。于是,我们六年级组的老师就做了这样的尝试,把课堂还给学生,把思维和创造还给学生,采取先预习、探究的形式来学习。下面是孩子们自己研究的成果:
通过孩子们自学的成果,我们不难发现:不同层次的学生应该有不同的解决方法,假设法、砍足法、列举法等。接下去,我们采取每个同学选择一种解决方法,在微信群中讲解。最后,再次去观看视频,丰富补充学生的认知。
改变课堂,变教为学。让课堂的精彩真正属于学生的精彩,课堂的收获应该是学生有所收获。作为教师,我们应该给孩子留有独立思考的空间,让他们在数学思考中体验到学习数学的快乐,给予孩子充分交流的时间,让他们在交流中变得思维灵活、有深度。
是的,小学数学应该这样教。老师不仅“知其然”,还懂得无限广阔的“所以然”;眼里不仅有知识,心里更应该装着每一位学生走进课堂。课堂氛围应该是自由、自然、自主的。在这里,我们应该和孩子一起去感受层层剥茧的新奇与新鲜,体会柳暗花明又一村的惊喜,更应该感知数学错综复杂的关系下又如此的“殊途同归”……
如果说,上课是一次旅程,那么让我们匆忙的脚步放慢一点,慢一点,让每个邂逅都那么自然,那么彻底。美学家朱光潜先生说:“慢慢走,欣赏啊!”数学教学,就是要让每个学生都知其然,更知其所以然,知其所以必然。在“知然”的过程中,触摸数学学习最美丽的风景!

