塔吊附臂附着力应用计算的研究

杨皓东， 吴 哲

(安徽建筑大学 土木工程学院，安徽 合肥 230601)

0 引 言

附着式塔式起重机附臂承受塔机运行时的施工荷载和塔身受到的风荷载,是保证塔机施工安全的重要结构,其产生的附臂力和附墙处附着力是工程施工中重要的参数,正确合理的附臂力和附墙处附着力不仅能保证塔式起重机自身稳定和正常运行,还能在减少建筑物结构设计上成本的同时使建筑物的质量和安全得到保证。但在实际工程中,塔机附臂力受到风荷载、自重、吊物重量以及动荷载的影响,而这些荷载具有不确定性,同时计算理论不成熟,因此计算难度较大。塔式起重机说明书虽然给出了附着力的部分参考数据,但其附着形式是固定的,计算模式未做明确说明,且这些参数一般适用于传统现浇结构，有大量成功案例证明其是安全可靠的。但对于装配式建筑而言,附着处墙体刚度较传统现浇结构明显降低,盲目套用这些参数存在很大安全隐患,因此需要对附着力进行研究,选择合理的计算模式,确定最不利的工况,使计算出的附臂力及附墙处附着力合理且偏于安全，以满足施工应用。

1 实例概况

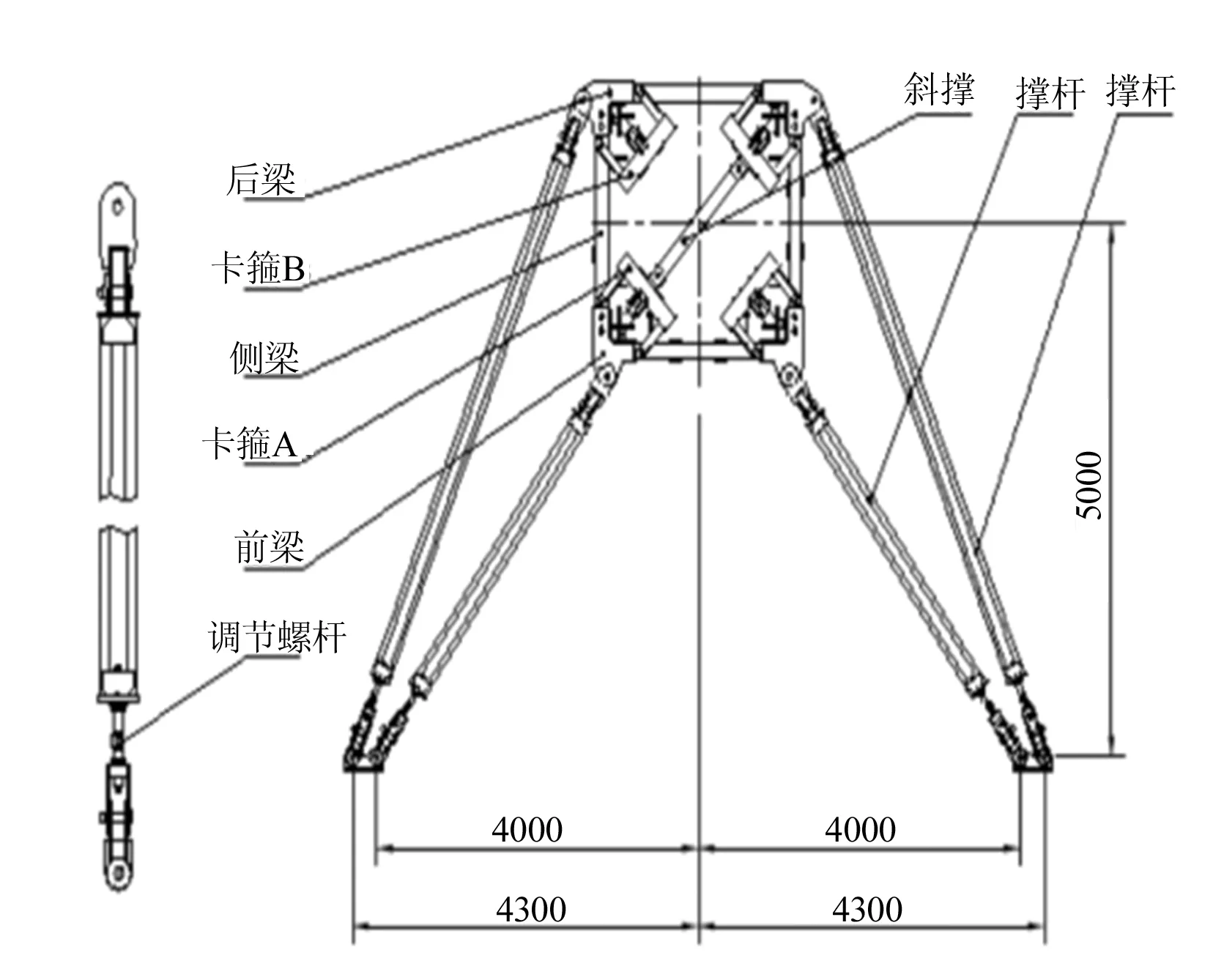
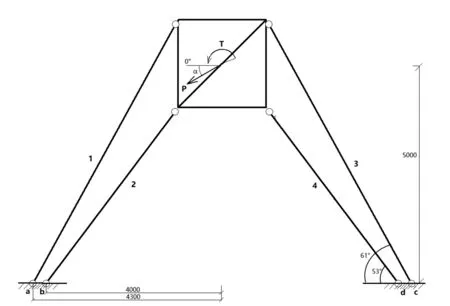
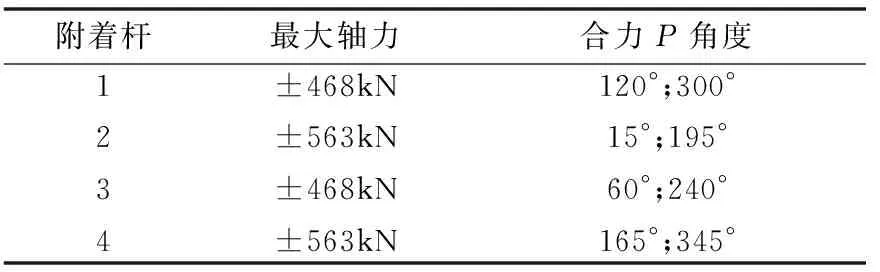
安徽蚌埠某装配式住宅建筑工程施工采用长沙中联重工科技发展股份有限公司生产的TC752516D型独立式塔式起重机:最大工作幅度75 m,独立高度51.3 m，最大工作高度240.3 m,第一道附着架以下塔身高度为33 m

预制装配式混凝土结构总高度为57 m,装配率为51%。塔机实际使用2道附着,第一道附着高度33.15 m,第二道附着高度54.3 m,悬挑高度27 m(塔顶高度为10 m),最终高度81.3 m,起重臂为75 m起重臂,平衡臂为20 m平衡臂,满配平衡重。

2 计算模式

根据塔机实际布置,计算模型中假定塔机基础为固定支座,附臂与塔身和建筑的连接方式为铰支座,桁架式塔身竖向刚度无限大可视作杆件,塔身悬挑部分仍看作悬挑结构。塔机起重臂、平衡臂、平衡重以及吊重所产生的自重荷载和施工活荷载,根据其重心离塔身中心距离,转化为不平衡力矩M作用在塔身上。风荷载q为均布荷载垂直作用在塔身上,为了方便计算并使结果偏于安全,假定风荷载始终与起重臂平行。此时,计算模型为一个作用有均布荷载和集中力矩的超静定连续梁(图1)。先对此模型使用结构力学求解器进行求解,可以得到虚拟支座X2和虚拟支座X3的反力PX2和PX3。此反力PX2和PX3就是由风荷载和不平衡弯矩所引起的4根附臂反力的合力。

图1 塔机超静定计算模型

塔吊工作时,起重臂可以360°旋转,此时会产生一个扭矩T,对附着力产生影响,所以在计算中予以考虑。假定塔身为一个刚体,反力作用于塔身中心,附臂与塔身和附墙节点的连接为铰接,如图2所示，其计算模型如图3所示。由图中数值可计算出附着杆1和附着杆3长度为6.85 m,与墙面的夹角约为61°,附着杆2和附着杆4长度为5 m,与墙面的夹角约为53°,图3中合力P(合力P方向为起重臂指向)可为任意角度,计算时逆时针进行360°旋转,扭矩T可为正负。

图2 附墙装置图

图3 附墙计算模型

3 最不利工况探究和计算

计算塔吊附着力,需要确定一种最不利工况。假定风荷载与起重臂平行,塔吊运行时会起吊重物,且起重臂旋转时会产生扭矩,所以塔吊工作状态较非工作状态不利,但由于附臂力和附墙处附着力受起重臂角度影响,还需进行后续计算才能得出附臂力和附墙处附着力最大值,确定其最不利工况。

3.1 不平衡力矩的计算

起重臂、吊重、平衡臂和平衡重产生的弯矩值为其重量m乘以重心到塔身中心的距离D。

起重臂自重产生的弯矩为M1=148.35×30.2=4 480 kN·m;最大吊重产生的弯矩为M2=160×15.5=2 480 kN·m;平衡臂自重产生的弯矩为M3=101×10=1 010 kN·m;平衡重自重产生的弯矩为M4=210×18=3 780 kN·m。

不平衡弯矩M=M1+1.35M2-M3-M4=3 038 kN·m[1.35为起升动力系数,根据《塔式起重机设计规范》(GB/T 13752-2017)]。

3.2 风荷载计算

风荷载标准值应按照以下公式计算:

wk=βz×μz×μs×w

wk=1.51×2.00×2.40×0.25=1.81 kN/m2

式中:w为基本风压,按照《建筑结构荷载规范》(GB 50009-2012)的规定采用w0=0.25 kN/m2;μz为风压高低变化系数,地面粗糙程度B类,高度为100 m,μz=2.00;μs为风荷载体型系数,根据塔架选取,μs=2.40;βz为风振系数,根据公式βz=1+2gI10Bz1+R2计算,βz=1.51;

塔身受到的风荷载:

q风荷载=wk×B×Ks=1.09 kN/m

式中：B为塔身标准节宽度,B=2.00m;Ks为迎风面积折减系数,取Ks=0.30,偏于安全。

3.3 附臂力及附墙处附着力计算

将风荷载q与不平衡弯矩M代入图1,使用结构力学求解器求解,得出虚拟铰支座PX2=-203 kN,虚拟铰支座PX3=237 kN。

图4 结构弯矩及虚拟支座反力

平面外稳定,计算时应考虑塔身安装垂直度误差所导致的偏心弯矩产生的轴向附着力,参考《建筑施工脚手架安全技术统一标准》,支撑脚手架取3 kN,考虑桁架式塔身的特点,取为6 kN较为合理。

取最上一道附着进行计算,P=PX3+6 kN=243 kN,工作状况下扭矩T=919 kN·m,使用结构力学求解器将合力P从0°逆时针旋转,每隔15°进行一次计算以寻找合力P最不利角度,得到附着杆轴力最大值和附墙处附着力最大值及所对应的起重臂角度，见表1。

表1 附着杆最大轴力

采用双杆附着耳座,同侧2根附臂附着在同一个耳座上,此时节点a、b为支座A,节点c、d为支座B,对附墙处产生的附着力为2根杆件轴力之合,此时附墙处的最大附着力对应的合力P的角度不再是单个附臂力最大值对应的角度,设与墙面平行方向为X方向,与墙面垂直方向为Y方向,通过计算得到表2。

表2 附墙处最大附着力

根据工程经验,还应考虑一些特殊角度下的附墙处附着力,例如起重臂和某一根附着杆平行或平行于一侧2根附着杆与墙面夹角的平均值,两侧附着杆对称布置,表3只列出左侧A支座附墙处附着力。

表3 特殊角度下附墙处附着力

对附墙处附着力计算结果与塔吊说明书中给出的数值进行对比,结果见表4。

表4 说明书数值与计算结果对比

4 分析与结论

(1) 分析计算结果,与说明书提供的数值误差较小,说明本文提供的计算模式和计算参数选取是合理的。对于实际工程中计算塔吊附臂力和附墙处附着力具有参考意义。

(2) 对比计算结果,当风向与起重臂平行,塔吊起吊重物的同时旋转起重臂,在起重臂旋转至塔身的四个角的瞬间为最不利工况。

(3) 在实际工程中,考虑到墙体的受力变形,Y方向的附墙处附着力更为重要,会引起墙体的变形甚至是超出其受力范围引起裂缝,X方向的附墙处附着力适当考虑抗剪能力。

(4) 工程中建议采用双杆附着耳座,如果在同一侧使用两个单杆附着耳座,附墙处附着力会明显增大。

(5) 根据表2合力P(起重臂)的角度可以看出,当起重臂指向矩形塔身的四个角时,附墙处附着力较大。根据工程经验,将起重臂旋转至上文所提特殊角度时,FY方向附墙处附着力与最大值相差5.5%以内,实际工程中计算附墙处最大附着力可选取这些特殊角度计算以减少工作量。

(6) 进一步简化图3附墙计算模型,附着杆1、2连接于节点b,附着杆3、4连接于节点d,得到的FY方向附墙处最大附着力，与本文计算结果误差为+8%,计算时可以考虑进一步简化。

(7) 塔吊附着对于传统现浇结构,已有大量成功的工程案例,但对于装配式混凝土结构,附着处墙体较传统现浇结构薄弱,需要慎重考虑,应对附着处墙体进行适当加强。

5 结束语

本文对附臂力和附墙处附着力的计算结果为后续的研究与设计提供了条件。工程中会根据附臂力和附墙处附着力进行一系列设计,包括附着杆、附墙耳座、预埋钢板和附着处墙体的设计,以确保塔机安全运行及建筑物的安全和质量。对于装配式建筑,还需对附着边缘墙体进行验算,确保其在施工中不会破坏。