一类受媒体报道影响的随机SIRI传染病模型的定性分析

刘变红，刘桂荣

(1.吕梁学院 数学系，山西 离石 033001；2.山西大学 数学科学学院，山西 太原 030006)

0 引言

众所周知，传染病是一个全球性的公共卫生问题.人们常用数学模型来进行数量预测和介入评估，如文[1-3].而在实际生活中，传染病模型自然会受到外部环境的随机干扰，因此对研究在随机因素影响下的随机传染病模型所具有的性质显得尤为重要，见文[4-6].近期许多学者在随机传染病模型中加入一类媒体函数[7]来刻画媒体报道对传染病的影响，显然这在传染病的预防和控制中具有一定的实际意义.本文考虑了如下受媒体报道影响的随机SIRI传染病模型

(1)

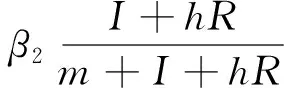
关于模型(1)的特殊情形，许多文献已作过研究.如文[9]研究了如下确定SIRI模型

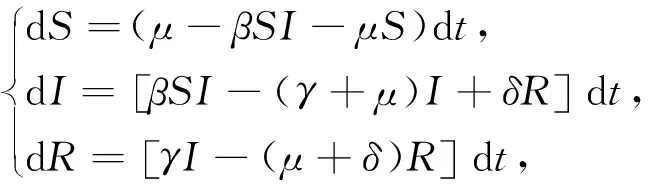
的基本动力学性态.随后文[10]研究了如下具有媒介影响的随机SIRI模型

全局正解的渐近性质.受以上结果的启发，本文对模型(1)的动力学性态进行研究，推广了已有文献中的一些结论.

1 预备知识

令(Ω，F，{Ft}t≥0，P)表示带有滤波{Ft}t≥0的完备概率空间，且滤波{Ft}t≥0满足一般的条件，即它是不减的，右连续，且F0包含了所有概率为零的集合.假设Bi(t)(i=1，2，3)定义在该概率空间上.此外，若X(t)是随机微分方程

的d维It过程，其中，F:Rd×[t0，)→Rd，G:Rd×[t0，)→Rd×m.任意V∈C2，1(Rd×[t0，);R+)，定义函数LV为

利用It公式，得

dV(X，t)=LV(X，t)dt+VX(X，t)G(X，t)dB(t)，

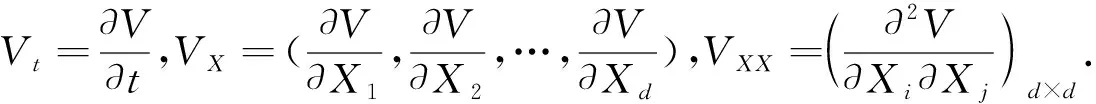
(2)

2 主要结果

下面给出本文主要结果及其证明.

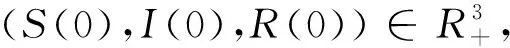
证明证明方法类似于文[10]中定理2.1的证明，这里略去.

定理2若R0≤1，且

σ1<μ，σ2<2μ，σ3<2μ，

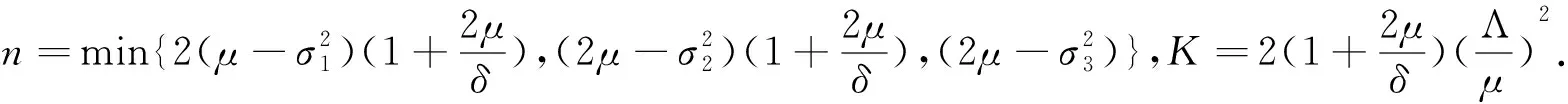
证明定义C2函数

V(S，I，R)=V1+xV2+yV3，

其中，x，y，z是待定正常数，且

利用It公式，有

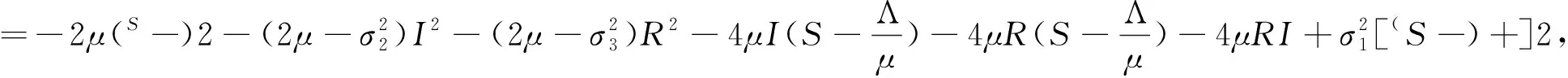
运用基本不等式(a+b)2≤2a2+2b2(a，b∈R)，得

(3)

(4)

而

≤β1SI+[zγ-(μ+γ)]I+[δ-z(μ+δ)]R

因为R0≤1，选取合适的z，使得

又I，R>0，则有

(5)

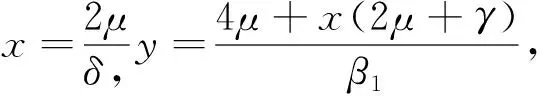
(6)

利用It公式，知

所以，可得

dV=dV1+xdV2+ydV3

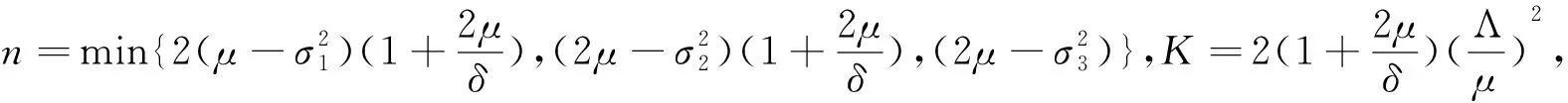
(7)

这里，M(t)是一个鞅，定义如下

对式(7)两端同时除以t，并令t→，则可得

几乎处处成立.

注 特别地，若σ1=σ2=σ3=0时，则式(6)变为

由Lyapunov方法知，当R0≤1时，确定性系统(2)的无病平衡点E0是全局渐近稳定的.

定理3若R0>1，则系统(2)存在唯一的地方病平衡点E*=(S*，I*，R*).

证明令系统(2)的每个方程右端为零，地方病(S*，I*，R*)满足S*>0，I*>0，R*>0，且

(8)

则

将S*，R*的表达式代入式(8)的第一个方程，得

A(I*)2+BI*+C=0.

其中，

由于R0>1，β1≥β2，且A≤0，C>0，则系统(2)存在唯一的地方病平衡点E*=(S*，I*，R*).

注 当h=0时，定理1-3变为文[10]中定理2.1、3.1、4.1.从而本文结果推广了文[10]中的相应结果.

3 结论

鉴于随机SIRI传染病模型的理论和实际意义，本文考虑了一类带有旧病复发和受媒介报道影响的随机SIRI传染病模型，利用It公式和Lyapunov方法等相关理论证明了该随机系统全局正解的存在唯一性，并得到了围绕无病平衡点的解的渐近性质，且证明了地方病平衡点的存在唯一性.当参数h=0时，本文结果与文[10]中相应结果一致，从而本文结果推广了已有文献中的相应结果.此外，假设模型(1)的每个方程中的参数β1受到一些随机干扰，即模型(1)变为如下新的模型

(9)

对于模型(9)的动力学性态的研究，需要克服更多的困难，可以作为我们进一步的研究工作.