钢管拱桥缆索吊装施工中主索结构状态高精度计算
蒋玮,李莘哲
(广西路桥工程集团有限公司,广西 南宁 530000)
1 引言
钢管混凝土拱桥是一种利用自己特有的结构形式来使钢筋和混凝土材料优劣势得到充分互补与发挥的一类桥梁。通常来说,在钢管内部被混凝土填充的状态下,这一结构的承载力明显大于其组成部分各自的承载力;另一方面,在钢管与混凝土共同受力的情况下,钢筋保持稳定平衡的能力也得到了积极的改变。
在钢管拱桥施工中,因适用性良好、设备调运灵活方便、跨越能力大等优势,缆索吊装法得到了施工单位普遍的认可与采用。通常来说,缆索吊装法的基本原理是在项目现场沿主桥轴线设置塔架及缆索系统,运用吊索塔架系统和稳定系统(揽风索、扣索)相互配合的一套方法,一片一片地把钢管拱肋通过跑车与起重索吊至设计位置并安装,直到拱肋合龙。随着中国桥梁施工技术的提升,缆索吊装系统越来越广泛地应用于大型桥梁的建设,并且这套系统将随着桥梁跨越能力越来越大、吊装重量越来越重、吊装系统性能越来越强大等趋势逐渐发展完善,因而,对缆索吊装过程进行精确计算分析,了解吊装过程中主索结构状态的变化规律,从而确保整个吊装过程高效、安全地进行,是非常重要的。
2 工程概况
广西马滩红水河大桥横跨来宾市区附近红水河,为主跨336 m的中承式钢管混凝土双幅拱桥。该桥桥面梁为钢-混凝土组合梁,引桥长210 m,全桥长553 m,主跨拱肋和格子梁采用缆索吊装系统安装。如图1所示,此套缆索吊装系统中跨为460 m,柳州岸边跨382 m,南宁岸边跨318 m。采用主扣合一塔架,塔底固结。柳州岸与南宁岸塔架分别设在其拱座后方和引桥桥台后方路基上。拱肋从南宁岸引桥下起吊,格子梁从南宁岸河滩上起吊。在索道承重方面,这一套施工系统配置了两组设计吊重为100 t的索道。

图1 缆索吊装总体布置图(单位:m)
此套系统的主索主要配置了两组承载索,并且每组主要承载索的设计吊重为500 kN。单组主索由5根半径为50 mm的密封钢丝绳组成,其抗拉强度为1 370 MPa,弹性模量为130 000 MPa,单根钢丝绳截面面积1 790 mm2,最小破断拉力2 366 kN。每组索的理论承载能力750 kN,即500 kN的额定吊重加上跑车、起重牵引钢丝绳、吊具等设备重量250 kN。
3 主索垂度
如图2所示,缆索系统主索可以被视为三跨连续钢索。假设在塔顶顶端主索不会产生相对滑移(即被认定为固定),同时忽略塔架偏位对主索的影响,简化并视主索为只有一跨的索线,如图3所示。
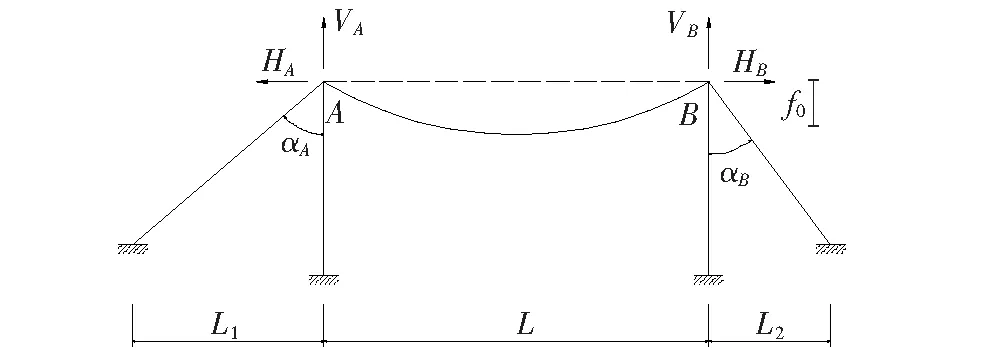
图2 主索结构示意图
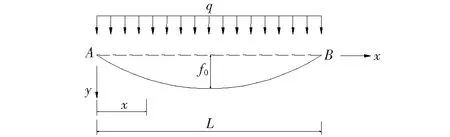
图3 未承重状态下主索计算简图
主索自重作用下任一点垂度可以表示为:
fx=Mx/H
(1)
式中:Mx为对应简支梁弯矩;H为主索水平力。
由于该受力状态下主索任一点水平力保持不变,可将式(1)转变为:
(2)
式中:f0为主索自重作用下跨中垂度,为25 m。
主索微段长度可表示为:
(3)
利用泰勒公式,并近似计算,可将式(3)转换为:
(4)
主索曲线弧长为:
(5)
缆索吊装过程主索结构状态计算简图如图4所示,根据跑车作用位置将主索分成两部分,分别称为主索Ⅰ和主索Ⅱ,将它们视为左右塔架高度不同的主索来分析。图中f1为当跑车运行至节点1时主索所产生的垂度,f2、f3分别为主索Ⅰ和主索Ⅱ中间位置节点2、3处主索的垂度。
节点1、2、3对应简支梁弯矩分别为:
(6)
(7)
(8)
垂度f1、f2、f3的关系为:
(9)
单独分析主索Ⅰ,如图5所示,图中m、n为区分主索计算设立的坐标轴,主索Ⅰ任一点垂度可表示为:
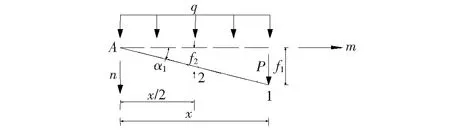
图5 主索Ⅰ计算简图
(10)
主索Ⅰ任一点纵坐标可表示为:
n=fm-mtanα1
(11)
式中:α1为主索Ⅰ与水平方向夹角,有tanα1=f1/x。
主索Ⅰ曲线弧长为:
(12)
由于主索Ⅰ在节点1处存在集中力P,相对于主索的求解而言,集中力P使得主索Ⅰ垂度减小,从而使得主索Ⅰ曲线弧长减小,因而,需要对式(12)进行修正,修正后的弧长公式为:
(13)
式中:M4=qx2/8为主索Ⅰ对应简支梁跨中弯矩。
同理,经过推导,主索Ⅱ的曲线弧长可由下列公式表达:
(14)
式中:M5=q(L-x)2/8为主索Ⅱ对应简支梁跨中弯矩。
主索在自重和集中荷载作用下索长可表示为:
S′=S1+S2
(15)
假设主索的长度在拱肋起吊和运输过程中不产生变化,即S=S′,综合式(5)、(13)、(14)和(15)可得到主索垂度f1在整个吊装过程中的变化情况,进而也可以对主索在系统进行载重运送过程中的结构变形情况有所了解。
运用Matlab编程软件对马滩红水河特大桥主索进行计算分析,得到在吊装过程中主索垂度随跑车位置的变化曲线,如图6所示。

图6 主索垂度与跑车运行变化关系图
由图6可知:跑车移至跨中时,主索垂度最大,最大计算垂度为28.18 m,马滩红水河特大桥现场实际测量最大垂度为27.76 m,由于该文将跑车作为一个节点计算,实际中跑车有10 m的轴距,所以该文的计算结果比实际垂度偏大,但该文的计算精度依然很高,可以应用于实际工程。
4 主索索力
主索索力在吊装过程中较为复杂,不同跑车位置,主索索力不同,且同一结构状态下,主索不同位置处的索力也不相同。下面对主索索力进行推导分析,从而了解吊装过程中主索索力的变化情况,对缆索系统的设计以及吊装中的安全把控有着重要的作用。
主索在自重作用下索力可表示为:
(16)
式中:H0=ql2/8f0为主索Ⅱ对应简支梁跨中水平分力;V0=q(L/2-x)为主索各点竖向分力。跨中竖向分力为0,因此自重作用下,主索索力T0=ql2/(8f0)。
主索无应力索长可表示为:
(17)
式中:E、A分别为主索弹性模量和截面面积。
起吊运输过程中主索索力可用下式表示:
(18)
引入以下关系式:
(19)
式中:H为主索索力在水平方向上的分量;β为主索与水平线的夹角。
综合式(13)~(19)可得到主索索力在整个吊装过程中的变化情况,利用Matlab数学软件求解分析,并结合实际工程所测数据,对主索索力随跑车位置而变化的理论与实测值进行对比,结果如图7~9所示。
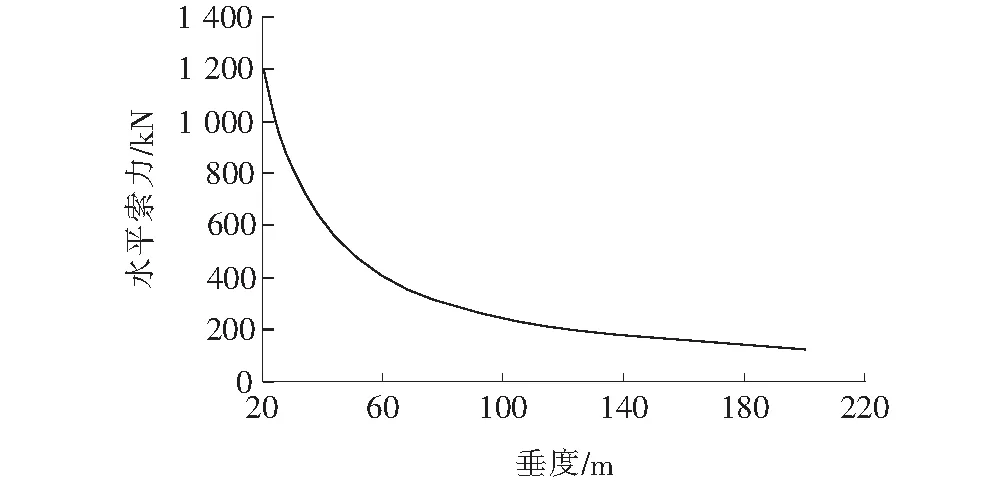
图7 主索水平索力与其垂度曲线图
由图7可知:主索索力随着垂度的增大而逐渐减小,并且随着垂度的增大,索力因垂度改变而受到的影响变得越来越不明显。但垂度的增大会缩减缆索吊装的作业空间,所以在进行缆索系统设计时,需要综合考虑结构受力特性及作业空间来设计合理的垂度。

图8 主索理论索力与跑车运行位置关系图

图9 实测主索索力与跑车运行位置关系图
表1为主索索力的理论计算值与实际值对比。
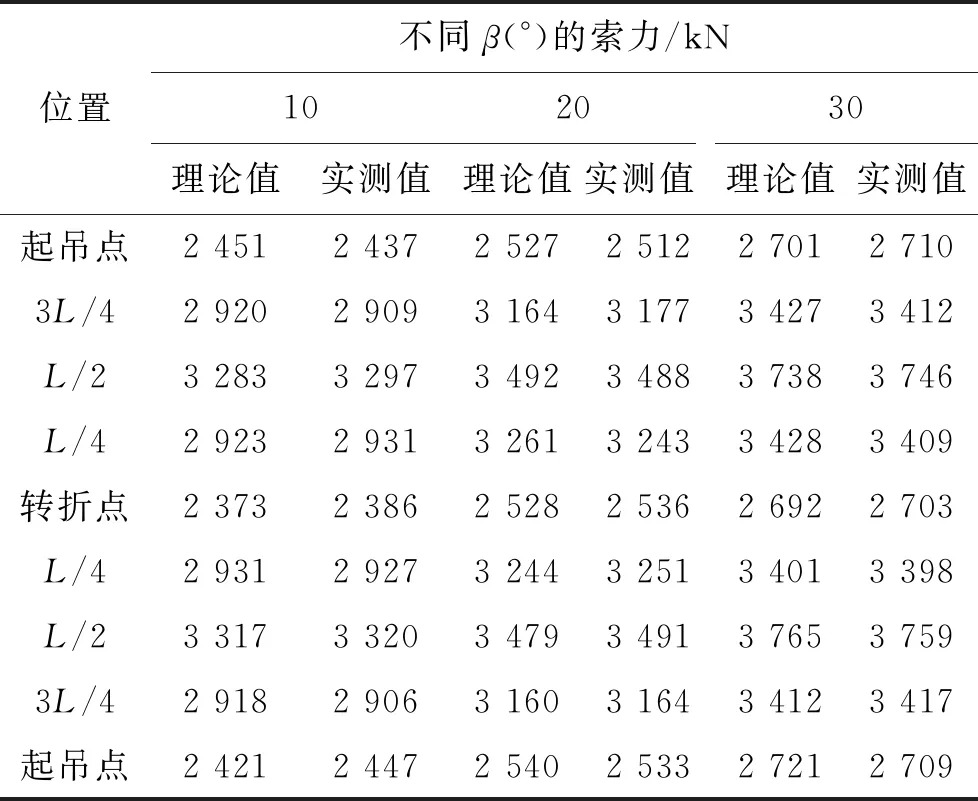
表1 主索索力理论计算值与实测值对比
由图8、9可知:当夹角β为定值,且索力T为平均索力时,主索上的索力将随着跑车从塔架向跨中移动而渐渐增大,并且当跑车运行至主索中点时其达到最大值。索力随着夹角β增大而相应增大。在拱肋起吊运输过程中,跑车行走至主索中点时索力达到最大值。
由表1可知:实际工程中索力随着跑车位置改变而改变的情况大体与该文推论相同,其误差为5%左右,即说明主索索力随着跑车移动而呈抛物线变化,并当跑车位于跨中位置(2L/4)时达到最大值,推导结果与实际情况大体吻合。
5 结论
通过理论推导及数值仿真对缆索吊装系统主索垂度、索力进行了计算分析,得到如下主要结论:
(1) 该文提出的主索垂度计算方法精度较高,可应用于实际工程。
(2) 在对主索进行设计时可适当增大垂度来优化主索受力,但随着垂度的增大,其对主索索力的影响将会逐渐变小,且垂度增大减小了缆索吊装作业空间,需要综合考虑来设计合理的垂度。
(3) 在缆索吊装过程中,主索索力随着跑车向跨中移动而逐渐增大,因此,跑车位于跨中时主索索力最大。

