关于大数定律的简单注解
陈傲星,武 靖
(华中师范大学 数学与统计学院,武汉 430079)
1 引言
抛一枚质地均匀且无损坏的硬币,正面朝上的概率是多少?50%,这是毫无争议的,也称为之先验概率①。如果抛这枚硬币两次,所得结果一定是一正一反吗?显然不是,两次为正或者两次为反的结果在生活中屡见不鲜。增加抛掷次数是否一定能得到一半正面一半反面的结果?历史上多位数学家通过试验给出答案。
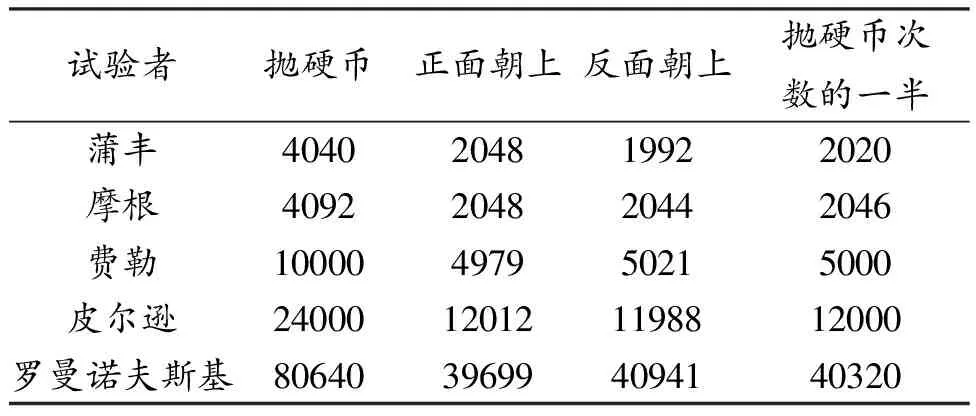
表1 数学家的试验结果
从结果看,虽然每一次试验中正面(反面)朝上的频数和抛硬币次数的一半不等,但是相差不大,并且随着抛掷次数的增加,前者在数值上稳定于后者。因此,投掷次数越多越有利于随机事件A统计规律的稳定表达。一般地,如果在n次相同的试验中,事件A发生的次数为k,当n很大,则k/n将接近于事件A的真实概率p。确定概率要比确定频率的难度大得多,因为概率可以看成随机事件的属性,频率是这一属性的表达结果;且绝大多数情况下,事件发生的概率难以通过逻辑分析或者历史经验获取,从而拿所掌握的频率信息推测概率不失为良策。频率是否等于概率?本质上不,但是大数定律告诉我们,当试验次数无限,即n趋近于无穷时,频率和概率是无限接近的。特别地,伯努利大数定律提供了用频率来确定概率的理论依据,由此我们可以用重复试验中某事件A出现的频率作为P的估计值。
2 伯努利弱大数定律
当人们发现抛硬币次数越多,“正面朝上”的频率越稳定的时候,某种规律呼之欲出。历史上第一个证明这个规律的人是伯努利。他在《推测术》中以“缶中抽球”②的例子来证明的。当然,抛硬币与缶中抽球本质上是一致的,为了不再引入新案例,我们仍选择引言中的事例。
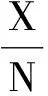
若换上式为
就是现今常见的弱大数定律的表达形式了。
当然伯努利证明大数定律的年代还没有方差这一概念,他在证明此定律的时候,先将犯错误大小ε限定为(a+b)-1,④必要时才按倍数缩小,此外他所使用的缶子模型也只能使得被估计的p值为有理数,但这并不影响定理的普遍性,可以推得对任意的ε、p都成立。伯努利大数定律的详细推到过程,有兴趣的可以参见文献[2]。当时,一个更直截了当的观点是:

3 强大数定律
波莱尔是法国数学家,他引进近代实变函数理论、测度论等,他所取得的成果,如波莱尔覆盖定理、波莱尔测度等,对现代数学的许多分支都产生了极其深远的影响。20世纪初,当波莱尔完成了对伯努利时代遗留下来的看似为真理的结论的证明时,强大数定律渐渐浮出水面⑤。而这些又要从两个有意思的引理说起。
波莱尔-坎泰利(Borel-Cantelli)第一引理:
设为某个概率空间的一个事件序列,若所有的事件发生的概率和是有限的,
那么它们之中有无限多个事件同时发生的概率为零,
波莱尔-坎泰利(Borel-Cantelli)第二引理:
设为某个概率空间中相互独立的一个事件序列,若所有的事件发生的概率和是无限的,
那么它们之中有无限多个事件同时发生的概率为1,
该引理的证明很简单,结合上极限的定义和集合论的知识即可⑥。直观上,若所有事件发生概率之和小于无穷,其同时发生的概率为零;当事件为独立事件时,反之亦正确。

4 强大数定律与弱大数定律的区别与联系
相信我们已经对伯努利弱大数定律和波莱尔强大数定律有了一个初步认识,抛开特定条件的大数定律,普遍意义上的强大数定律和弱大数定律有什么关系呢?
首先更一般地,大数定律分析的是一定条件下某随机变量序列的算数平均值收敛于某常数或常数列。为叙述上的方便,设ξ1,ξ2,…,ξn为一随机变量序列,ξ为常数或常数列。
从上文不难推测,强大数定律在相同的条件下较弱大数定律得出了更强的结论。直观上讲,前者认为这种不收敛现象只能偶尔出现,即有限的;后者允许无限次不收敛。
强大数定律和弱大数定律的区别从测度上讲,前者是“几乎确定收敛(almost surely convergence)”或者“以概率1收敛”、“几乎处处收敛”,后者是“依概率收敛(convergence in probability)”。若把不收敛于概率值的“坏点”放在一个集合D中,前者只允许D为零测集⑧,后者可以接受D的测度极小。一般地,两者前提条件相同,得出的结论不同。顾名思义,前者的结论更强。
为了更进一步探究,我们引入如下概念。
定义1. 以概率1收敛
设ξ和{ξn}为定义在概率空间(Ω,F,P)上的随机变量序列。若存在Ω0⊂F,P(Ω0)=0,且对任意w∈ΩΩ0,有
ξn(w)→ξ(w),n→∞
则称ξn以概率1收敛于ξ,记作ξn→ξ(a.s.)
定义2. 依概率收敛
设ξ和(ξn)为定义在概率空间(Ω,F,P)上的随机变量序列。若对任意的ε>0,有
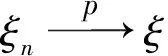
定义3. 强大数定律
设ξ和{ξn}为定义在概率空间(Ω,F,P)上的随机变量序列,且Eξn存在,若∀ε>0,有
则称ξn服从强大数定律。
定义4. 弱大数定律
设ξ和{ξn}为定义在概率空间(Ω,F,P)上的随机变量序列,且Eξn存在。若∀ε>0,有
则称{ξn}服从弱大数定律。
由定义出发,结合测度论的知识,不难发现以概率1收敛等价于几乎处处收敛,依概率收敛等价于依测度收敛,而几乎处处收敛蕴含依测度收敛,依测度收敛一般情况下不包含几乎处处收敛,因此依测度收敛是较弱收敛(见文献[2]),从而得出:基于依概率收敛的弱大数定律较弱于依托于以概率1收敛的强大数定律。事实上,若随机变量序列服从强大数定律,则其一定也服从弱大数定律,反之不成立。
5 经验分布函数与强大数定律
通过上述部分的介绍,大数定律从理论上肯定了“用频率估计概率”的合理性,同时也是“矩估计”的基础。事实上,它证明了随机变量的算术平均值以概率1收敛于数学期望,奠定了参数估计的一个重要法则。
但是大数定律的适用性是广泛的。这里再举一个漂亮的例子——经验分布函数的合理性。
经验分布函数是连接实际数据与理论分布函数的桥梁,是在n个数据点中的每一个上都跳跃1/n的阶梯函数。当样本量足够大的时候,其以概率1收敛于总体分布函数⑨。
定义5:设X1,X2,…,Xn为来自于总体X的容量为n的简单随机样本,X(1),X(2),…,X(n)为其顺序统计量,x1,x2,…,xn为其样本取值,样本取值确定时,样本顺序统计量随之确定。对任意实数x,


后来,格列纹科在此基础上又给出了更强的结论,他证明了经验分布函数与理论分布函数偏移量的最大值以概率1收敛于0,进一步肯定了经验分布函数的合理性,同时也说明还存在比强大数定律结论强度更大的规律。大数定律支撑下的经验分布函数应用广泛,比如最大熵模型中用作约束条件、金融资产对数价格中潜在现货方差的分布形式等,更有研究者以此提出了确定样本量的新方法(见文献[6])。
6 结论
大数定律从理论上赋予了频率更大的意义,使其不仅仅是某一次试验属性的象征,更是概率的良好估计。条件相同,结论也可能不同。强大数定律和弱大数定律正是基于结论性质的强度划分,前者是以概率1收敛,后者是依概率(测度)收敛。强大数定律和弱大数定律下有许多不同的提法,比如强大数定律下的波莱尔大数定律、柯尔莫哥洛夫大数定律;弱大数定律下的伯努利大数定律、切比雪夫大数定律、马尔科夫大数定律、辛钦大数定律……这些定理的条件有差别,结论各异,共同构成了大数据时代绚烂的光彩。
注释:
①先验概率,是指根据以往经验和分析得到的概率。文中抛硬币一次,其正面朝上的概率为1/2是通过分析计算而来.
②缶中抽球,即缶子模型:缶中有a白球,b黑球,有放回地从缶中抽球N次,记录抽白球的次数为X.
③伯努利引进了“道德确定性”的概念,若某事件有极大的可能性以至几乎不会不发生,则存在道德确定性。这一概念现在也叫“事实上的确定性”(practical certainty).
④伯努利的证明基于缶子模型,a,b是既定量,详见注2.
⑤强大数定律和弱大数定律是后来人们为了区分不同结论的大数定律根据其结论的强弱程度划分的,本文为了方便起见直接引用现在的名字.
⑦当n趋于无穷时,可视S1,S2,…为一个无穷的伯努利试验序列,其中每一事件只依赖于有限次试验。又由于抛掷行为是独立的,满足第二引理中要求的独立性.
⑧这里的零测集,根据实际意义更可以排除其为零测集中无限集的情况,或根据波莱尔-坎泰利第一引理证明其为零测集中的有限集.
⑨总体分布函数,即理论分布函数:F(x)=P{X≤x},是随机变量X小于某常数x的概率.

