矩阵体积的特性及其应用

陈荣群

(莆田学院 基础教育学院，福建 莆田 351200)

0 前言

矩阵体积的定义是Adi Ben-Israel于1992年在Linear Algebra and Its Application上发表了一篇名为《A volume associated with m×n matrices》的文章中首次提出。该文章中给出了矩阵体积不仅是矩阵行列式绝对值的推广，也是向量长度的推广，而且对任意的矩阵都有相应的体积；并且他在文[2]-[3]中给出了利用矩阵体积计算曲线与曲面积分、推广勾股定理、计算维球面的面积以及n维球体的体积；利用变量替换公式又给出了矩阵体积在概率论方面的应用。

目前对矩阵体积的研究主要是在矩阵体积的应用、矩阵体积与初等变换的关系、矩阵体积与矩阵标准形的关系方面，文[4]中又给出上三角矩阵、伴随矩阵的体积，但对矩阵体积的性质研究还不是很多。因此本文在理解矩阵体积的概念的基础上，对矩阵体积的有关性质作进一步研究，分别探讨两个矩阵和、差、积的体积与两个矩阵体积的和、差、积大小关系，以及探讨矩阵张量积的体积、循环矩阵的体积，最后探讨应用矩阵的体积来判断正交矩阵，从而使矩阵体积的性质、应用能得到进一步的完善。

1 预备知识

先介绍矩阵体积及其相关的一些概念与符号。

Qr,m={I={i1,i2,…,ir}r|i1≤i2≤…≤ir≤m}表示{1,2,…,m}中依次增大的r个数的集合。

I(A)={I∈Qr,m|rank(AI*)=r,AI*表示矩阵A的最大的行线性无关向量组}表示A中最大的行线性无关集合的指标集。

J(A)={J∈Qr,n|rank(AJ*)=r,AJ*表示矩阵A的最大的列线性无关向量组}表示A中最大的列线性无关集合的指标集。

N(A)={(I,j)∈Qr,m×Qr,n|rank(AIJ)=r}表示A中最大的非退化子矩阵集合的指标集。

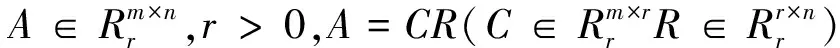
引理1[1]N=I×J

引理1表明：任意r个线性无关的行和任意r个线性无关的列的交所得到子矩阵是非退化的。

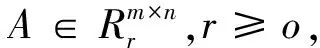
定义3[6]n阶实矩阵A，若满足AAT=I，则称A为正交矩阵。

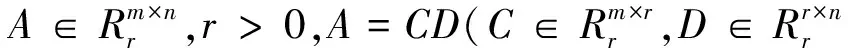
引理2[5](1)设A∈Rk×m,B∈Rp×s,C∈Rm×n,D∈Rs×q,则有(A⊗B)(C⊗D)=(AC)⊗(BD). (2)如果A,B都是正交矩阵,则A⊗B也是正交矩阵。

2 主要的结果及其证明

性质2.1 设A∈Rm×n，B∈Rm×n，rank(A+B)=rank(A)=rank(B)=1

则volA+volB≥vol(A+B).

因为rank(A+B)=rank(A)=rank(B)=1，由矩阵体积的定义得

所以(volA+volB)2≥vol2(A+B)，从而得到volA+volB≥vol(A+B) 证毕。

推论1 设A∈Rm×n,B∈Rm×n,rank(A-B)=rank(A)=rank(B)=1,则volA-volB≤vol(A-B)

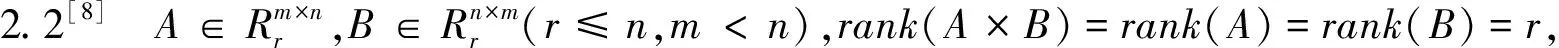
证明 由引理3得 设C=AB，则乘积C的子式

由引理4得

所以(volA×volB)2≥vol2(A×B)，从而得到volA×volB≥vol(A×B) 证毕。

对于A⊗B的行列式和A，B的行列式有下列的关系：det(A⊗B)=(detA)n(detB)m,其中A∈Rm×m,B∈Rn×n．对于A⊗B的体积和A，B的体积也有类似的关系，即有如下的性质：

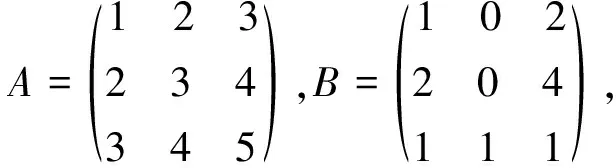
解 ∵rank(A)=2,

=6.

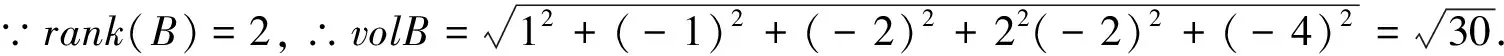
由性质2.3得vol(A⊗B)=vol2A×vol2B=36×30=1080.

其中f(x)=a0+a1x+a2x2+…+an-1xn-1,

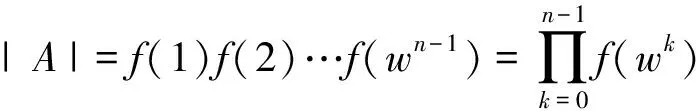
由于a0,a1,a2,…,an-1为互不相等实数，且a0+a1+a2+…+an-1≠0,xn-1与f(x)=a0+a1x+a2x2+…+an-1xn-1互素。

所以f(1)≠0,f(wi)≠0(i=1,2,…,n-1)从而得到A可逆，rank(A)=n，

性质2.5 设循环矩阵

n为正奇数，ai=a0+id1(a0>0,d1>0,i=1,2,…,n-1),bi=b0+id2(b0>0,d2>0,i=1,2,…,n-1)，则vol(A+B)>volA+volB.

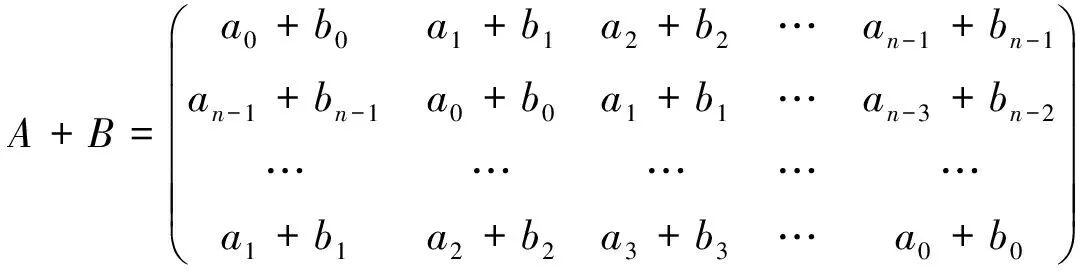
设f(x)=a0+a1x+a2x2+…+an-1xn-1,g(x)=b0+b1x+b2x2+…+bn-1xn-1,f(x)+g(x)=

(a0+b0)+(a1+b1)x+(a2+b2)x2+…+(an-1+bn-1)xn-1,

因为ai=a0+id1(a0>0,d1>0,i=1,2,…,n-1)，对单位根u=wk≠1总有

f(u)=a0+a1u+a2u2+…+an-2un-2+an-1un-1,

f(u)-uf(u)=a0+d1(u+u2+…+un-1)-an-1=a0-d1-[a0+(n-1)d1]=-nd1

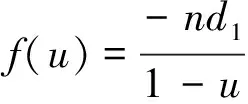
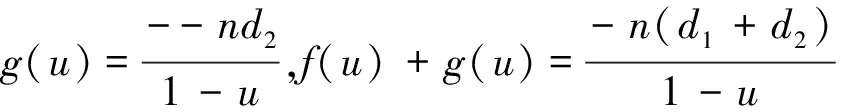
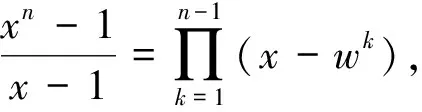
|A+B|=[f(1)+g(1)][f(w)+g(w)]…[f(wn-1)+g(wn-1)]

=(-1)n-1[f(1)+g(1)]nn-2(d1+d2)n-1

∵ai>0,bi>0(i=0,1,2,…,n-1),n为正奇数，

∴|A+B|>|A|+|B| 由性质2.4得vol(A+B)>volA+volB证毕。

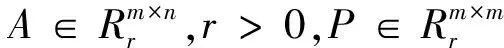
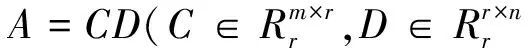
同理可得:

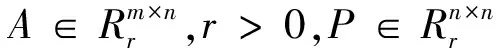
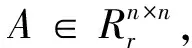
由于rank(ATEijA)≤min{rank(A),rank(Eij)}≤1,且

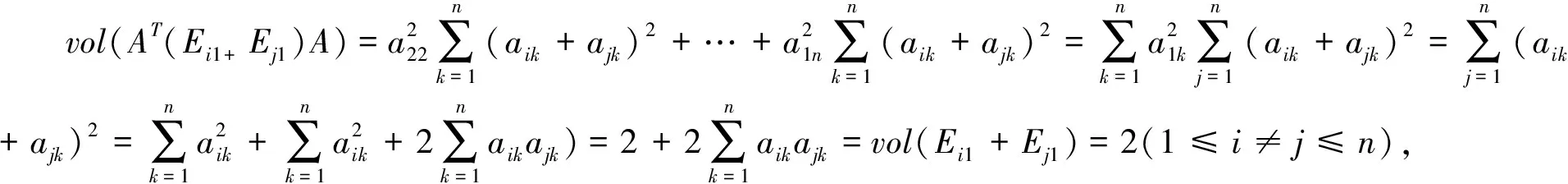
所以A是一个正交矩阵. 又由引理5、引理6知正交矩阵不改变矩阵体积，所以结论成立。