一种钢箱梁弯曲剪应力的有限元分析方法

2020-06-05 03:26陈宝春

山西建筑 2020年12期

陈宝春

(上海市政工程设计研究总院(集团)有限公司，上海 200092)

0 引言

钢箱梁结构目前被广泛应用于桥梁结构。钢箱梁属于闭口薄壁结构，抗扭刚度大，整体性较好；但钢结构壁板较薄，剪切变形效应大，剪力滞效应明显，正应力分布不均，不符合平截面假定。同时，多箱室结构的腹板弯曲剪应力求解，为超静定问题，给实际工程中的应力计算带来了难度。

本文根据对实际工程设计经验的总结，提出如下近似计算方法：

1)根据钢箱梁壁板剪力变形协调条件,利用线单元有限元法求解剪力流大小及自由剪切变形。

2)根据上述有限元法求解所得的箱梁翼缘板剪切变形，结合箱梁内力的分布特点，近似计算剪力滞效应。

根据经典薄壁结构力学理论，在竖向荷载作用下，梁的弯曲变形符合平截面假定，忽略剪切变形，箱梁截面正应力分布沿截面高度方向呈线性分布；剪应力的分布，与正应力分布协调平衡。

传统力学求解方法[1]实际为确定剪力流0点位置的超静定力学问题：将截面假定若干开口，将结构假定为开口截面，在开口处作用未知平衡剪力流，利用开口处剪切变形协调条件，求解该组位置平衡剪力流，以求解剪应力分布。

这种方法为力法求解，简单直观，但在实际工程计算的计算机程序运算中，存在一定不便，即钢结构截面的箱式布置自由度较高，力法方程需要人为指定求解超静定次数及冗余约束，适用性有一定欠缺。

本文根据钢箱梁属于薄壁结构的特点，根据有限元法，在截面所在的竖直平面中，将板划分为线单元结构组，求解剪力流，基本假定如下：

1)将节点沿垂直截面方向的位移设为自由度。

2)根据平截面假定，将线单元在沿梁纵向的正应力增量设为外荷载。

3)忽略线单元在平面方向的剪切变形，根据线单元平面外的剪切刚度建立单元刚度矩阵。

4)建立矩阵方程求解剪力流大小。

根据上述假定，将截面中板单元模拟为如图1中所示。

图1中，单元节点位移及外力说明如下：

dZ1,dZ2分别为单元左节点(x1，y1)、右节点(x2，y2)处在垂直于截面方向产生的位移，mm；dσ1,dσ2分别为在剪力Q作用下产生的左节点(x1，y1)、右节点(x2，y2)处垂直于截面方向正应力变化率，MPa/mm。

板元刚度矩阵如下:

其中，G为剪切模量。

以单箱单室截面为例，按上述有限元方法计算，进行算例说明。选取结构断面如图2所示。

将结构进行单元划分，共计单元16个，节点16个，按照节点关系，汇总刚度矩阵及求解信息如表1所示。

根据所求解得位移，反算板元剪应力，得出截面在剪力作用下的剪力分配结果，如图3所示。

在考虑剪切变形后，截面产生垂直于截面方向相对剪切变形，该变形使截面不符合平截面假定，从而影响截面的正应力分布，即剪力滞效应。同样以上述算例为例：对所求得的剪切变形进行修正：1)使其满足该变形在全截面产生的正应力总和为0；2)使剪切变形对中性轴产生的竖向矩总和为0。

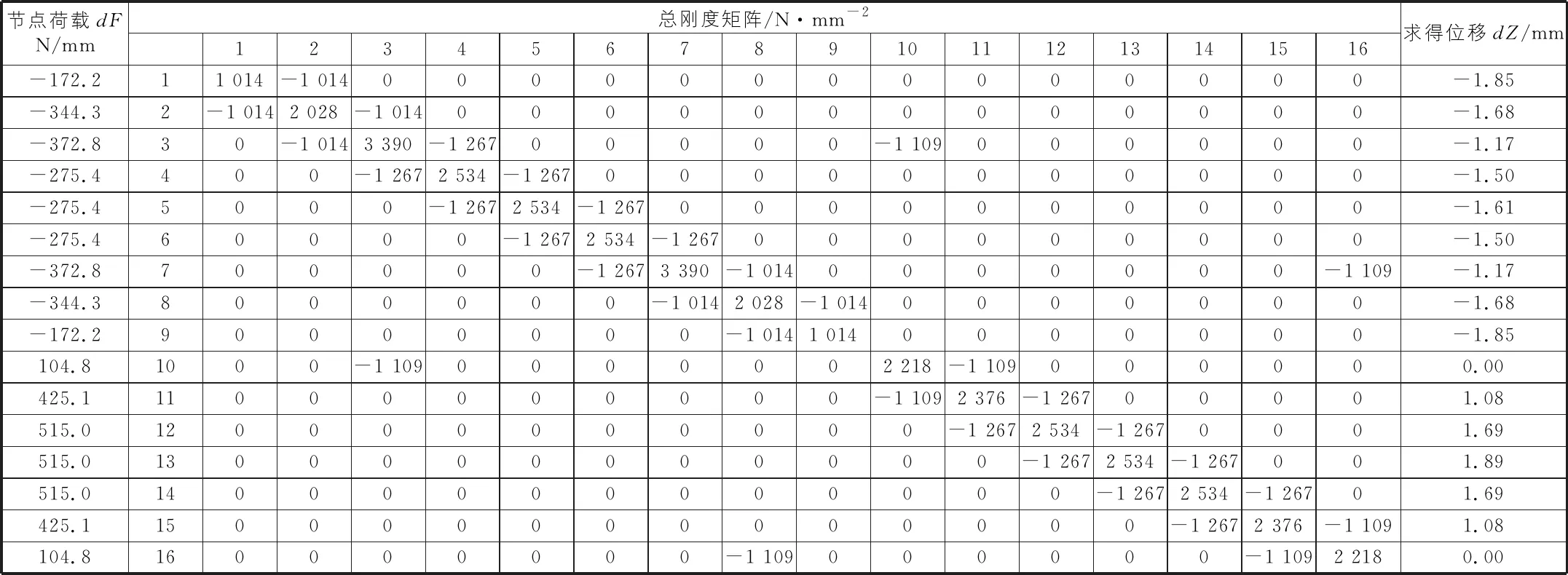
表1 总体刚度矩阵及计算结果表

将上述算例的板元细化，求得修正后的变形形状如图4所示。

剪力沿梁轴线变化产生上述剪切变形的变化，由此产生次生正应力，及剪力滞效应。

用公式表达：σ=σ1+σ2，其中，σ1为符合平截面假定的弹性弯曲正应力；σ2为剪切变形产生的次生正应力；z为梁轴向坐标。

以30 m跨径简支梁为例，在跨中受集中荷载作用下，荷载作用位置处，产生剪力突变，为满足剪切变形连续的变形协调条件，假定剪切变形在剪力突变点附近以3次抛物线分布，对于本算例渐变段长度左右各取6 m，分布见图5。

由上述方法求解考虑剪力滞效应的跨中弯曲正应力，如图6所示。

板壳有限元计算方法可以反映出剪切变形效应，但由于实际工程应用中，桥梁钢结构大多构造复杂，且需要利用动态规划加载来进行活荷载分析，边界约束条件及外荷载的取值及模拟也较为繁琐。因此，在现有的计算机及工程软件效率的条件下，在桥梁设计的过程中，板桥有限元方法“成本”较大。

本文结合传统梁结构计算理论，提出将梁截面特性中，将前述的截面剪切相对变形，作为新的有限元几何自由度，引入到现有梁单元有限元计算中，并由此自由度的求解来反映梁截面的剪应力分布及正应力不均匀性，得出满足实际工程精度要求的计算结果。

但这种方法存在如下问题，仍需进一步讨论:

1)在剪切变形的整体表达式中，未考虑板在横桥向及竖向的剪切变形，这些变形与板件的横桥向和竖向应力相互耦合，在梁单元计算中如何考虑这些因素，值得进一步讨论。

2)桥梁结构的板元通常设置较多的加劲板，使得这些板元在拉压及剪切刚度的计算中，存在异性板特征，如何考虑加劲板在截面特性计算中的贡献，值得进一步讨论。

3)在集中荷载作用下的剪切变形的突变长度计算方法，值得进一步讨论。