基于宏观环境下的“顺势而为——GARP”投资策略

金展颖，沈淑琦

一、引言

自2018 年年初以来，我国对外贸易出口有所减缓，市场经济环境稍有动荡。 从宏观来看，面对多变的市场环境，我国积极采取措施进行调整和应对，加速经济转型升级，并通过调整国际贸易结构和产业结构，鼓励国内战略性产业发展。 这些政策深入人心，且对国内资本市场带来积极影响，投资者应顺应国家政策走向，采取顺势而为的投资策略。 本文基于当前的宏观政策条件，选择优势行业，利用GARP-均值方差模型构建投资组合策略，通过EViwes 进行投资组合收益的t检验和股票的相关性检验，从而保证投资组合在去除伪相关的前提下获超额收益。

二、现实与理论基础

(一)震荡市场下的股市投资

基于震荡的市场环境，中国股市的动荡让不少投资者受到了较大的影响。 很多投资者也在寻找政策的走向，但由于自身相关知识的缺乏与获取利益欲望的差距，而陷入过度自信或信心不足的困境，难以形成正确的投资策略，因此，需要一个科学有效的理论框架指导。 很多研究已证明政策变化会对企业投资、总需求、金融风险溢价等产生显著影响(Pástor ＆ Veronesi， 2013)；例如，Bernanke(2015)认为，经济环境和政策的不确定性增加会导致经济主体的风险厌恶程度上升，风险溢价随之大幅上升。 以长生生物为例，医药行业的良好发展前景吸引了众多投资者购买其股票，然而在被曝出该厂生产的医用设备存在质量问题后，相关的惩治措施和出台的各种举措大大打击了行业信心，而当时看好此股的不少股民也纷纷被套……由此可见，我国股市发展多与国家政策调控息息相关，近年来，政府大力支持和发展5G 行业，并推动基建工程的建设，也为通信板块带来了蓬勃生机，其股价不断创历史新高。 因此，如何能在灵活多变的市场环境下获取更高收益，逐渐成为众多投资者思考的问题。 本文正是基于此，提出了“顺势而为”的选股策略。

(二)价值与成长性的GARP模型

“合理估值下的成长”，即GARP 投资策略。 此策略在量化投资领域广泛应用，且具有较好的风险收益比。 Ahmed 和Nanda(2001)选择低市盈率和高盈利增长率股票的策略(实质上是 GARP 投资策略)，利用美国 1982 年至 1997 的股票数据，发现在风险调整基础上，这种新策略优于传统的低市盈率投资策略，由此他们认为价值和成长投资策略不应相互排斥，可以融合成 GARP 策略。 沈浩(2009)在我国沪深 A股市场运用GARP 模型对股票进行筛选并构建GARP 组合，通过分析研究发现该模型在我国A 股市场同样有效，并指出运用GARP 投资策略存在两个潜在的收益渠道：①价值回归过程中的投资收益；②成长特性实现期间引起的股票实际价值的提高。 但Larkin(2009)将通过模型筛选获得的股票组合与市场的收益衡量指标进行比较之后发现虽然GARP 策略并不总是表现优异，但可以考虑在其投资组合中至少对一部分股票组合使用 GARP 策略；而董伟炜(2019)在传统GARP 策略上加了两层约束，一是嵌入成长曲线形态，优先选择景气加速的行业或公司；二是更多地考虑“市值空间”。

基于上述描述，本文结合政策取向和行业结构，提出GARP-均值方差选股策略。 以宏观经济走势作为切入点，选取与当前国内环境紧密相关的几个行业，利用专业方法对各行各业的基本面和技术面进行分析，并结合分析结果，运用模型构建出领跑大盘的股票组合，在引导投资者正确认识上市公司股票的价值属性和成长属性的同时，运用专业的方法帮助投资者寻找最具潜力的股票，实现价值投资的真谛——具备从丑小鸭到黑天鹅变化的被低估的股票；最后运用专业的手段和检验方法佐证所得结果，保证价值投资最大化的正确性。

三、改进的GARP均值方差模型

传统的GARP 模型兼顾股票的价值属性和成长属性，在分享高成长带来的收益机会的同时，寻求安全边际。 但是其过度看重成长的稳定性，会错过行业景气度较好、高速增长的企业股票。 因此，我们对该策略进行了进一步的改良，创建了“GARP-均值方差”策略。 主要有以下三个方面的改进：其一，根据宏观背景确定行业，选择国家政策大力扶持和宏观环境波动下影响较小的行业；其二，筛选出七大指标均高于行业均值的个股，并结合序数打分法，适当调整指标所占比重；最后，利用方差最小化的原则，构建股票组合。

(一)改进GARP-均值方差模型应用步骤

1.确定股票池

以总资产同比增长率、净资产同比增长率、营业收入同比增长率、营业利润同比增长率、ROA 增长率、EPS 增长率、预测PEG 值七大指标对行业板块进行初选，得到七大指标均高于行业均值的个股。

2.采用序数打分法

将选用的财务指标进行打分排序，从而确定指标得分的秩值。 本文在选取过程中依据不同行业特点计算平均值，目的是在宏观市场中寻找最具潜力的成长股；据此选出的投资组合暗含了宏观经济周期对于行业配置的优化结果。 综上，通过金融终端将满足初选财务指标的个股统计出来之后，对这些个股的财务指标进行排序，按秩打分，公式如下：

其中，P为分数；N表示每项指标的最高分；Y表示样本总数；Xt表示样本t秩。

(1)分值设定

总资产同比增长率、净资产同比增长率、营业收入同比增长率、营业利润同比增长率、ROA 增长率、EPS 增长率得分满分均为10 分，按顺序打分，即增长率越高，得分越高；预测PEG 得分为10 分，按倒序打分，即指标越大，得分越低。

(2)权重设定

传统的GARP 策略价值指标和成长指标一般各占50%，考虑到中国A 股市场成长股往往比价值股更能够取得较大收益以及中小投资者偏爱成长股投资的环境，在指标的选用上，成长型指标占比达到90%的比例，而价值型指标只占10%的比例。 选用的指标和权重比例如下：一是成长规模指标。 选用的是总资产同比增长率、净资产同比增长率和营业收入同比增长率，在权重上各占10%；二是成长质量指标，由于成长质量往往比规模更重要，本文选用的是营业利润同比增长率、ROA 增长率和 EPS 增长率，各占20%的权重；三是安全估值指标。 选用的是预测PEG 值，PEG 值介于0～2 之间，在权重上只占10%。

3.构建组合

选取筛选后的股票，统计2017 ～2019 年的收盘价数据，利用马科维茨的均值-方差模型，以最小化股票组合的风险来计算股票的投资比例。

以两只股票为例：

得到一个关于WA的函数(1-WA)σAσBρAB求导时，取得最小值，解得WA＝同理，n支股票时同理也可建立n-1 个导数方程最终求解出n个投资组合的投资比例系数。

4.定期调整组合

持有组合一至两个月后，根据行业总体经营情况，适当调整指标；利用更新的数据指标对股票池重新进行筛选。

(二)模型应用实例

1.股票筛选

根据行业差异，结合当前市场环境所设置的条件为大致为总资产同比增长率≥20%，净资产同比增长率≥10%，营业收入同比增长率≥20%，营业利润同比增长率≥10%，ROA增长率≥5%，EPS 增长率≥5%，预测 PEG 值介于 0 ～2 之间(时期不同的市场所设置的参数需以当时市场数据变动为依据)。 根据数据筛选出的结果，可得到被低估的股票，从各行业中再选取1～2 只龙头股进行具体的数据分析。

2.股票组合的构建

根据近两年来四个行业的个股收盘价计算相关系数，得出不同行业之间的个股也存在较强的相关性。 相关系数如表1 所示：

表1 股票相关系数检验表

当数据为正值时，可以认为不同行业之间的不同个股相关性较强，而数据为负时，不同行业之间不同个股的相关性比较弱。 此外，可根据相关系数矩阵图，用EViews 软件进行显著性检验，以去除伪相关的可能性。

根据表2 可知，F值为174.4542，去除了伪相关的可能性，证明结果显著。

表2 伪相关检验结果

股票组合的检验过程如下：

(1)二元函数且相关系数小于0

(2)二元函数相关系数大于0

(3)三元函数

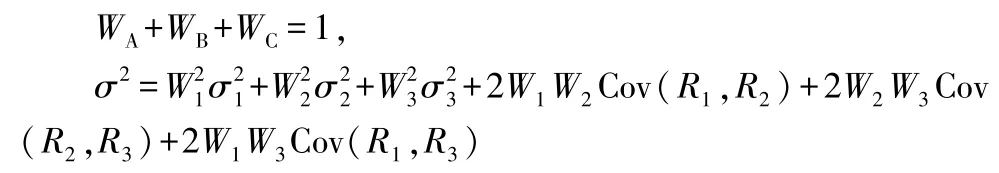
联立可得σp＝f(W1，W2)。

求解两个方程，即可得到σp取得最小值时W1、W2投资组合比例。

(4)N元函数

同理将8 只股票的数据代入上述方程，并利用8 只股票的投资组合比例为1，即可转化为方差最小的情况下7 个未知数求解的问题。 分别将风险函数关于7 个未知数进行求导数，并联立求解7 个方程即可解得对应的投资组合比例，因实际求解过程过于复杂，仅在此说明求解方法。

根据以上对投资组合的构建，可得其具体的2019 年投资组合如表3 所示。

表3 投资组合的构建

以上表3 只是部分买卖股票组合，具体操作时不局限于以上几种。

在均值-方差模型中，我们发现当两只股票相关系数为负的情况下，同时买入一定比例的股票，可以对冲风险，并且使得风险最小化；当两只股票相关系数为正的情况下，买入一只股票并卖空另一只也能达到分散风险的目的，这时候的操作就等同于买入两只相关系数为负的股票。 综上所述，在股票投资组合的过程中，不能随意决定股票的投资组合比例，而是在充分考虑单只股票的风险与收益的同时，还要顾及股票之间的相关性和具体的相关系数，利用相关性来减小风险。 通过模型量化计算，来获得个性化的投资组合比例，从而使手中资产发挥最大的价值。 股票投资组合对于任何一个股市参与者而言，都有非常重要的作用。

四、总结与讨论

根据上述模型的构建和相应操作，本文初步建立了在当前市场经济环境下相对较优的选股策略，力图用创新选股模型为选股难题带来解决之道。 据此，本文依据已经选取出的股票组合收益与沪深300 指数收益率进行对比，得到投资组合收益情况如图1 所示：

图1 组合收益与沪深300 收益对比

t 检验结果的prob 值＝0.028，显著小于0.05，则参数的显著性检验通过，再看R2，越接近1，拟合优度越高，此模型R2值为0.76，说明拟合程度较好； DW 检验用于残差序列的相关性，DW 取值在2 附近，说明残差序列不相关。 t 检验的结果显示：在99.9%的水平下，组合的收益明显高于同时段沪深300 指数，与我们的原假设相符合。

本文基于当前的市场环境，选取受到相关政策以及民族情绪推动增长的行业，再利用GARP 模型对公司价值属性和成长属性进行探索，在获取拥有成长属性的股票收益的同时，放眼价值属性被低估的股票，争取超额收益。 同时，利用GARP 模型选择出的股票进行相关系数计算，推出均值-方差模型，构建投资组合，在保证收益的同时，也能大大降低投资组合的风险；最后，用EViews 软件对投资组合的收益进行显著性检验，确保投资收益跑赢大盘的同时，找到适合当前股市形势的最佳投资组合。