具有时变时滞的Lur’e系统的新的同步条件

吴叶繁，熊良林，柳莹莹，王 珍

(云南民族大学 数学与计算机科学学院，云南 昆明 650500)

0 引 言

近20年来，混沌系统的同步问题引起了学者们的关注[1-5]，原因是同步在动态网络、信息安全、生物系统、电子电路等诸多领域有着广泛的应用和研究前景.很多动力学系统比如蔡氏电路、古德温模型都可以转化成Lur’e系统来处理，Lur’e系统是一类重要的非线性系统，它由一个线性部分和一个满足扇区界限的非线性部分组成[6].因此，很多学者对混沌Lur’e系统的同步问题进行了研究[7-12,24].此外，时滞广泛存在于网络控制系统、电路系统、化工系统等各种实际系统中，它的存在往往会导致系统性能变差甚至出现不稳定现象.综上所述，研究具有时滞的Lur’e系统的主从同步问题十分有意义[7-21,24].

近期，为了实现相关系统的同步，学者们发展了诸多控制方法，比如反馈控制[12-21]、采样控制[10]、脉冲控制[24].文献[10]利用采样控制器，结合新构造的分段可微LKF，研究了Lur’e系统的主从同步问题.当使用反馈控制来实现时滞Lur’e系统的同步时，文献[14]通过建立一个新的Lur’e-postnikov型李雅普诺夫泛函，结合使用詹森不等式进行处理，得到几个时滞依赖同步判据.文献[12]在构造LKF时使用了时滞分割法，并用詹森不等式对LKF的导数进行放缩，从而得到具有更低保守性的充分条件.文献[19]通过将三重、四重积分引入到LKF中，结合使用詹森不等式技术，获得了比文献[12]保守性更低的结果.可以看到，文献[14,12,19]通过使用各种方法如时滞分割、多重积分，得到了很好的结果，然而作者在处理LKF时，使用了詹森不等式.众所周知，詹森不等式虽然有效但是会带来一定的保守性[19].为了尽可能地克服这个保守性，以获得更大的时滞上界，学者们近期得到了一系列重要的不等式[22-23,25-30].比如文献[27]通过构造函数的方式，改进了詹森不等式，推出了一个名为Wirtinger-based的新不等式.基于此，得出了一些新的稳定性条件.借助自由矩阵的思想，文献[28]推导了一个新颖的自由权矩阵不等式，它包含詹森不等式和Wirtinger-based不等式.利用自由权矩阵不等式，建立了保守性更低的稳定性条件.最近，文献[22]的作者利用一组不完全正交的多项式函数，推导出一个含有更多自由矩阵的新积分不等式，该不等式的特点是可以提供更多交叉项信息和增加更多自由度.文献[28]中的自由权矩阵不等式是文献[22]中的新积分不等式的一个特例，基于这个新不等式[22]，文献[22]得到了更好的结果.因此，本文拟基于文献[22]中的新积分不等式处理技术，结合构造更符合系统的新LKF，获得时滞Lur’e系统保守性更低的同步条件.

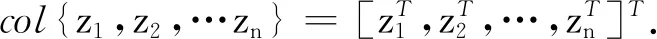
1 预备知识

1.1 系统描述

考虑一般的带有反馈控制的时滞Lur’e主从同步系统模型：

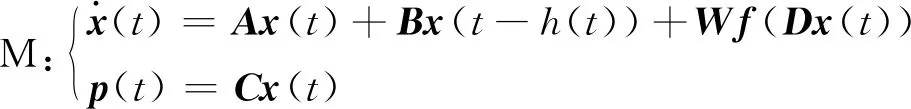
(1)

C:u(t)=K(p(t-h(t))-q(t-h(t)))，

其中M，S，C分别表示该模型的主系统、从系统和控制器；x(t)，y(t)∈Rn表示系统的状态向量，p(t)，q(t)∈Rl是系统的输出向量；A，B∈Rn×n，D∈Rm×n，W∈Rn×m，以及C∈Rl×n是已知的实数矩阵；当输入控制u(t)=0(u(t)∈Rn)时，M，S是2个相同的Lur’e系统，K∈Rn×l表示待定的控制器增益矩阵；时变时滞h(t)满足如下条件：

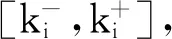
(2)

假设误差信号e(t)=x(t)-y(t)，则相应的误差系统可表示成：

(3)

其中η(De(t),y(t))=f(D(e(t)+y(t)))-f(Dy(t)).

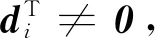
(4)

其中D=[d1,d2,…,dm]T，di∈Rn，i=1,2,…,m.

由(4)式，显然有：

(5)

1.2 引理

引理1[22]x(t)是一个可微函数：[a,b]→Rn.若对称矩阵U(∈Rn×n)>0，Z11，Z22，Z33，Z44∈R5n×5n，任意矩阵Z12，Z13，Z14，Z23，Z24，Z34∈R5n×5n，N1，N2，N3，N4∈R5n×n满足

则下面的不等式成立：

(6)

显然，不等式(6)中包含自由矩阵，这增加了不等式的自由度，不仅如此，还将提供更多的交叉信息，这些都可为降低保守性发挥重要的作用.

2 理论结果及证明

本节将构造一个符合误差系统(3)特性的新LKF，结合积分不等式(6)对其导数进行放缩，获得使误差系统(3)渐近稳定的新充分条件，从而得到使得主从系统(1)同步的控制器设计条件.

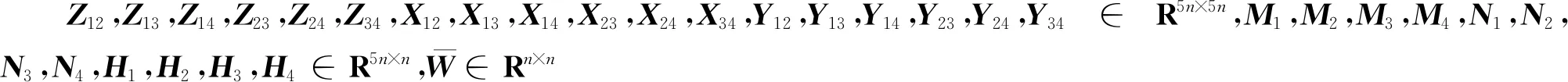
(7)

(8)

(9)

Q3-Q2<0,Q2-Q1<0,

(10)

ψ(h1,0)<0，ψ(h1,u2)<0，ψ(h2,u1)<0，ψ(h2,0)<0，

(11)

则误差系统(3)是渐近稳定的，从而主从系统(1)可以达到同步.其中

Π1=e1-e3，Π2=e1+e3-2e6，Π3=6e6-6e9，

Π4=2e1-12e6+30e9-20e12，Π5=e4-e5，Π6=e4+e5-2e8，Π7=6e8-6e11，

Π8=2e4-12e8+30e11-20e14，Π9=e3-e4，Π10=e3+e4-2e7，Π11=6e7-6e10，

e0=[0n×17n0n×m]，ei=[0n×(i-1)nIn0n×(17-i)n0n×m]，i=1,2,…,17，

控制器增益为：

证明：结合系统(3)的特性，本文选择如下的LKF

其中

对Vn(et,t)(n=1,2,3,4)沿着误差系统(3)的解的轨迹求导得：

(12)

(13)

(14)

(15)

(16)

另一方面，根据(5)式，对于正定对角矩阵L3∈Rm×m有下列不等式成立，

-2(η(De(t),y(t))-K-De(t))TL3(η(De(t),y(t))-K+De(t))≥0，

(17)

即

(18)

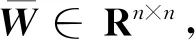
(19)

因此，根据式(12)～(19)可得：

(20)

综上所述，根据(11)式可以得到，误差系统(3)是渐近稳定的.证毕.

3 数值实例

我们把所推导的同步准则应用到蔡氏电路中，以说明本文方法的有效性和优越性.给出蔡氏电路方程如下：

(21)

从以下两种情况来说明本文条件的可行性和有效性.

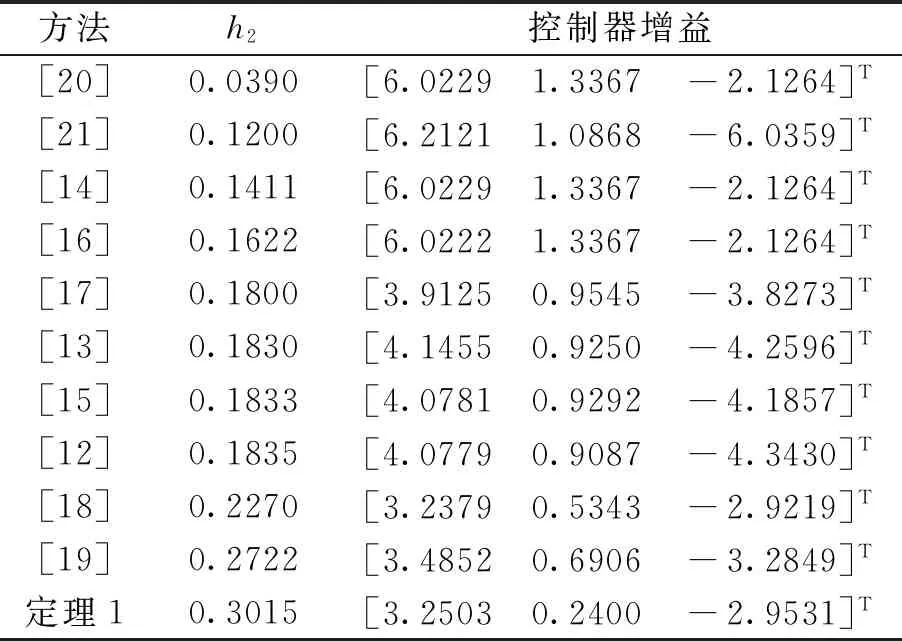
表1 当u1=u2=0,h1=0时，可允许的最大时滞上限及控制器

情况2：当h(t)为常时滞，我们有u1=u2=0，当r1=2，r2=1，h1=0，初值x(0)，y(0)的取值与情况1相同时，可解出h2的最大上界为0.3015,相应的控制器增益矩阵为K=[3.2503 0.2400 -2.9531]T.表格1列出了本文与近期一些文献结果的对比，从表格中可以看出，本文所得时滞上限与文献[12]，[18]和[19]相比，分别提升了64.3%，32.8%和10.8%.且当h2=0.3015时，相应的仿真结果被展示在图2-4中.图3和图4反应了当误差系统(3)中的控制输入u(t)=0时系统的混沌行为；图2描绘了当u(t)≠0(如K=[3.2503 0.2400 -2.9531]T)时误差系统(3)的状态轨迹，从图中可以看出系统(3)是渐近稳定的.定理1的有效性得到验证.

4 结语

本文探讨了时滞Lur'e系统的同步问题.首先，在充分考虑系统内部各个状态变量之间联系的基础上，构造出了一类新的多个包含增广向量的LKF.其次，使用一个新的自由矩阵积分不等式并结合时滞分割法去处理构造的LKF的导数.最后，通过一个数值实例来说明所得结论的有效性和优越性.本文方法还可以拓展到对具有马尔科夫跳跃的Lur'e系统的同步问题的研究中.