改进的无线传感器网络三边质心定位算法

李海啸，于 东，胡 毅，3，于皓宇

1(中国科学院大学，北京100049)

2(中国科学院沈阳计算技术研究所，沈阳110168)

3(沈阳高精数控智能技术股份有限公司，沈阳110168)

1 引 言

无线传感器网络(Wireless Sensor Network，WSN)由大量体积小、耗能少、价格低且具有计算、通信、存储甚至移动功能的传感器组成，这些传感器能够自发地感知环境、获取并处理数据，最终将数据传递到观察者［1］.WSN 的这种动态感知、处理和传递消息的能力使得WSN 被大量应用在需要反映现实世界某种特征的应用中［2］，例如:智慧工厂、环境监测、智能家居、军事侦察等领域.在这些应用中，无论是寻找数据源位置，还是对移动目标进行跟踪，WSN 节点定位技术都是非常重要的.但为WSN 的所有节点都安装GPS 以获得自身精确位置的方法是不现实的.目前常用的解决办法是给一部分节点安装GPS 或在初始阶段将这些节点设置在固定位置，其余节点利用这些特殊节点(称为锚节点)进行定位［3］.WSN 定位算法根据节点间是否需要测距可以分为两类［4］:基于测距(Range-based)和基于非测距(Range-free)的定位算法.基于测距的定位算法主要有:信号传输时间算法(Time Of Arrival，TOA)、信号到达时间差算法(Time Difference Of Arrival，TDOA)、信号到达角度算法(Angle Of Arrival，AOA)和接收信号强度指示算法(Received Signal Strength Indicator，RSSI).基于非测距的定位算法主要有:近似三角形内点测试法(Approximate PIT Test，APIT)、距离矢量跳数算法(DistanceVector Hop，DV-Hop)和质心算法(Centroid).上述各定位算法的主要优缺点如表1 所示.

由于目前大多数无线通信模块都支持RSSI 的测距功能，所以基于RSSI 的定位算法是一种低成本、易实现的定位方法.但其缺点是RSSI 信号传输容易受到外界因素(例如:障碍物、多径效应、噪声等)影响，导致RSSI算法存在较大定位误差［5］，因此通常采用相应的优化或修正算法来提高定位精度.本文在研究大量RSSI 三边定位算法的基础上，对传统的基于RSSI 的三边质心定位算法进行改进，通过采用模糊C均值聚类算法对锚节点发射到未知节点的多组RSSI 信号进行聚类，消除小概率大干扰的RSSI 信号，计算相对准确的未知节点和锚节点之间的距离，并且为弥补传统三边质心定位算法的不足，提出参考点加权质心定位算法，通过寻找合适的参考点对未知节点进行精确定位.

表1 WSN 定位算法比较Table 1 Comparison of localization algorithms for WSN

2 基于RSSI 的三边定位算法相关研究

目前，很多学者对WSN 基于RSSI 的三边定位算法进行研究并提出改进方法:文献［6］通过拟合区域的环境参数，对RSSI 值进行排序，找出可信度最高的前三个锚节点用于定位计算，采用加权质心定位的权重因子来反映锚节点对质心坐标决定权的大小和对质心位置的影响，提高了定位精度.但没有考虑三个锚节点接近于同一条直线而导致定位误差大甚至定位错误的情形.文献［7］提出一种基于RSSI 的三边定位聚类改进算法，该算法利用KMC+聚类优化方法对基于 RSSI向量的三边定位结果进行聚类，对每个聚类中心求平均值作为定位结果，减小了三边定位误差.但在基于RSSI 源数据预处理和聚类定位计算过程中并没有彻底消除RSSI 测距误差带来的影响.文献［8］提出了在使用高斯滤波算法对RSSI 信号进行滤波的基础上，为进一步提高三边定位算法精度和鲁棒性，提出了增加一个锚节点的四边形加权质心算法，并提出了直线方程法判断以两个锚节点为圆心的定位圆的交点是否为定位所需的内侧交点.虽然四边形定位算法在一定程度上提高了定位精度和鲁棒性，但所需计算时间和算法复杂度却随着锚节点数目的增加而大幅提高.文献［9］利用约束条件将目标区域内的锚节点进行筛选，选出与未知节点相关系数较大的锚节点，在相关系数较大的区域内对未知节点进行定位.文献［10］分析了基于RSSI 定位算法误差的两个主要来源:一是来自根据RSSI 信号衰减强度计算节点间距的理论模型或经验模型;二是来自RSSI 传输路径上障碍物的影响.提出了基于RSSI 的线上更新定位方法:首先利用距离未知节点最近的2 个锚节点得到未知节点的2 个可能位置，再利用较近的第3 个锚节点选择其中1 个位置作为定位结果，可以有效减小障碍物的影响并提高定位精度.文献［11］讨论了GPS技术在室内WSN 定位中面临的挑战以及三边定位算法在室内WSN 定位中的优点，在集成开发环境下利用智能手机和相应操作平台实现了室内三边定位技术的实验，最后验证了三边定位技术的合理性和延展性.

目前，基于RSSI 的三边定位算法由于无需额外的传输硬件、所需锚节点较少、耗能和成本低等优点被广泛应用于WSN 定位，尤其在室内、地下场所等GPS 信号很难到达的区域.但RSSI 定位算法容易受到周围环境或发射模块噪声脉冲等影响，定位误差较大［12］.因此如何提高基于RSSI 的三边定位算法的精度，是重点研究和解决的方向.

3 基于RSSI 的三边质心定位算法

WSN 基于测距的定位算法通过测量节点之间的距离或角度根据空间几何原理来实现对节点的定位，可以分为三边定位法、三角定位法、最小最大法、极大似然法等.三边定位法由于算法时间复杂度小、功耗少、成本低而被广泛应用.

3.1 基于RSSI 测距的定位原理

基于RSSI 测距的定位过程包括3 个阶段［13］:测距阶段、定位阶段、修正阶段.

阶段1:测距阶段.根据发射信号到达未知节点的强度计算锚节点和未知节点之间的距离.目前常用的测距理论模型为Shadowing 模型［14］(也称对数—正态分布模型):

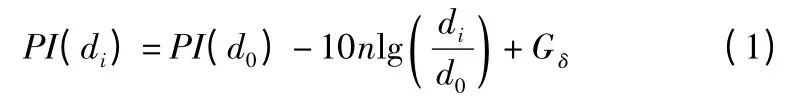
公式(1)中，PI(di)为距离信号发射端di处的信号强度，PI(d0)为距离信号发射端d0处(d0为参考距离，一般为1m)的信号强度，n 为路径衰减指数，Gδ为均值为0，方差为 δ 的高斯随机变量.经过化简并用RSSI(单位:dBm)表示di处的信号强度:

公式(2)中，A 是节点间距1m 时接收节点接收到的RSSI信号强度.公式(2)给出了RSSI 和di的函数关系，所以根据接收到的RSSI 就可以计算出两个节点的间距.环境参数A和n 都是经验值，和具体硬件、周围环境因素相关.RSSI 随着距离di的增加而减小，在短距离中衰减速度非常快，10m 以后开始逐渐趋于平缓［15］，所以短距离内利用RSSI 信号衰减强度测距的误差更小.

阶段2:定位阶段.在节点定位阶段，未知节点通过阶段1中计算的与锚节点之间的距离，根据基于测距的定位算法计算自己的位置，例如:极大似然法、三边质心法和最小最大法等.

阶段3:修正阶段.对定位阶段估计的未知节点坐标进行优化或修正，减小定位误差，进一步提高节点定位精度.由于本文只研究如何利用测距信息进行精确定位，只涉及前两阶段，故未对修正阶段展开讨论.

3.2 三边定位算法原理

三边定位算法简单，容易实现，但误差较大.虽然极大似然定位法可以利用三个以上锚节点的测距信息并通过最小二乘法在RSSI 测距误差平方和最小值的条件下得到未知节点的估计坐标，但由于距离越远的RSSI 测距误差越大，距离越近的RSSI 测距越接近真实值［16］，极大似然定位法没有对锚节点及测距距离进行有效区分，当距离过远的锚节点被选中参与定位时，很可能会增加定位误差.本文采用距离未知节点最近且非接近一条直线的三个锚节点参与定位，可以有效提高定位精度.三边定位算法基本原理如下:

假设未知节点U(x，y)通过接收三个锚节点M1(x1，y1)、M2(x2，y2)和M3(x3，y3)发送的RSSI 信号计算锚节点到未知节点 U(x，y)的对应距离 d1、d2和 d3.以 M1、M2和 M3为圆心，距离d1、d2和d3为半径画圆，得到三个定位圆之间的交点，定位原理如图1 所示.

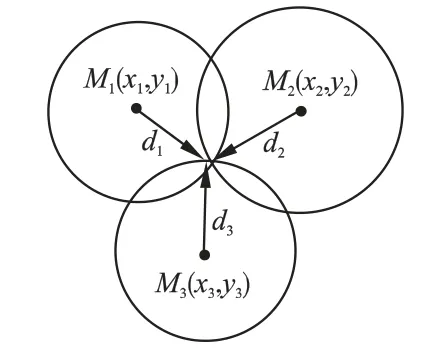
图1 三边定位算法原理Fig.1 Trilateration Localization Algorithm principle

根据两点间距离公式联立方程组:

方程组经变形和转换为矩阵形式:

得到未知节点的估计坐标为:

由于RSSI 容易受到噪声或环境等因素干扰，三个定位圆心有时并非相交于一点，而是两两相交，形成三个交点:D1(x1，y1)，D2(x2，y2)，D3(x3，y3).可以采用三边质心定位算法或三边加权质心定位算法估计未知节点的位置［17］，未知节点U(x，y)的估计坐标为:

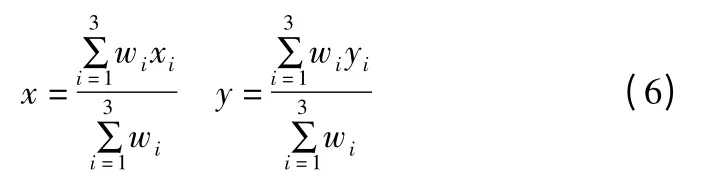
其中，wi为权值系数，大小一般与接收到的RSSI 信号强度正相关或与未知节点和锚节点的距离di负相关.当wi≡1时，公式(6)为三边质心定位算法定位结果，当wi=gi(d1，d2，d3)时，为三边加权质心定位算法定位结果.

4 改进的三边定位算法

由于RSSI 信号容易受到环境、障碍物和噪声信号的干扰，随机产生小概率大干扰的RSSI 信号，影响未知节点根据RSSI 强度计算与锚节点的距离，影响定位精度.本文通过对三个锚节点向未知节点发射多组RSSI 信号并利用模糊C 均值聚类方法进行聚类，消除小概率大干扰信号，得到准确RSSI 信号值计算未知节点和锚节点的距离，再通过参考点加权质心算法计算未知节点的位置.

4.1 双集合组合法寻找符合条件的三个锚节点

根据文献［18］，未知节点接收到的RSSI 值越大表明信号衰减越小，与发射信号的锚节点间距越小，所受环境和障碍物的影响也将越小，并且当3 个锚节点的位置近似成等边三角形时，定位更准确.距离越近、RSSI 值越大的锚节点在计算未知节点的位置时应有更大的决定权［19］.所以，三个锚节点的选择条件是发射到未知节点的RSSI 信号应尽量大，且三个锚节点的位置不接近一条直线.本文提出双集合组合法挑选符合条件的锚节点，具体步骤如图2 所示.

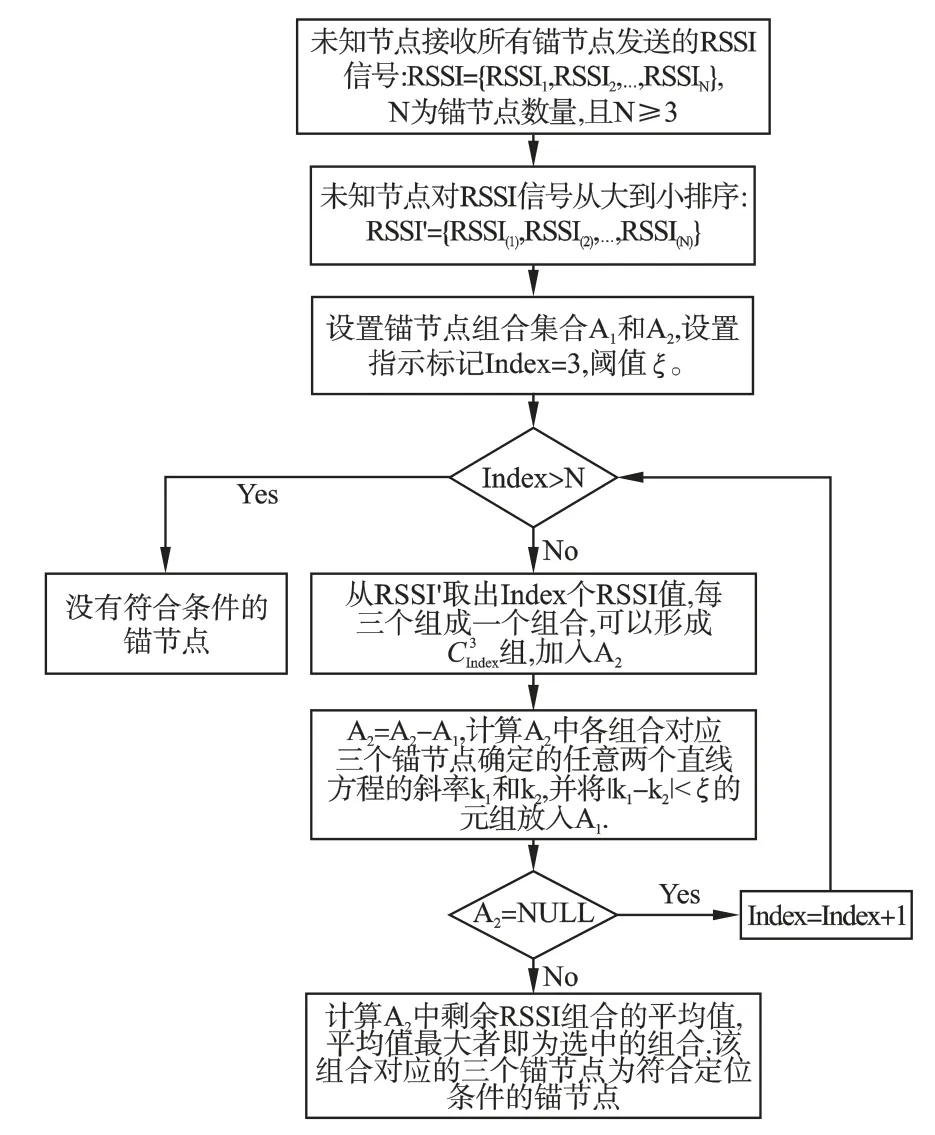
图2 双集合组合法寻找符合定位条件的锚节点Fig.2 Double-Set combination method to select localization-qualified anchor nodes

WSN 中所有锚节点向未知节点发送RSSI 信号，未知节点按信号强度对 RSSI 从大到小排序，例如:{RSSI1，RSSI2，…，RSSIN}，N 为未知节点接收到 RSSI 信号的个数，即通信范围内所有锚节点的个数.未知节点选中其中最大的三个 RSSI:RSSI1，RSSI2，RSSI3，由于对应锚节点的位置是已知的，例如:(x1，y1)，(x2，y2)，(x3，y3)，可以计算任意两个锚节点连接直线方程的斜率:

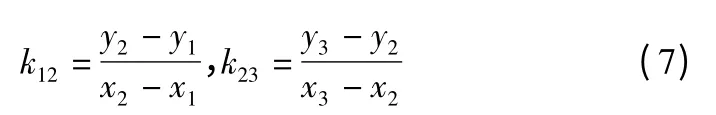
4.2 利用模糊C 均值聚类法计算RSSI 准确值

模糊C 均值聚类算法(Fuzzy C-Means Clustering Algorithm，FCMA)是用隶属度表示每个样本属于某个聚类程度的一种模糊聚类方法.该算法通过迭代的方式寻找使目标函数不断趋向更小值时的中心向量及隶属度，由于该算法容易陷入局部极小值，所以对隶属度初始值的选取依赖程度很高.而量子粒子群优化算法(Quantum Particle Swarm Optimization，QPSO)具有全局空间搜索能力，可以在全局空间寻找最优解，不易陷入局部极值，因此本文利用量子粒子群优化算法的全局搜索代替模糊 C 均值聚类算法的迭代过程计算最优解［20，21］.

三个锚节点向未知节点发射三组RSSI 信号，假设每组信号数量为M，可以组成M 个RSSI 观测值三元组，也称样本三元组.RSSI 信号矩阵如下所示:

R 是由三个锚节点到未知节点的所有RSSI 信号观测值组成的矩阵.需要根据基于量子粒子群算法的FCMA 对R 进行聚类，消除小概率大干扰的RSSI 元组.

在量子粒子群优化算法中，设定粒子数为N，维数为d，粒子向量为Xi=(xi1，xi2，…，xid)，粒子每次计算两个最优位置进行移动:一个是粒子截止目前自己的最优位置，又称个体最优位置Pi=(pi1，pi2，…，pid)，另一个是粒子群截止目前的最优位置，又称全局最优位置 Pg=(pg1，pg2，…，pgd).为提高全局搜索能力，引入平均个体最优位置:

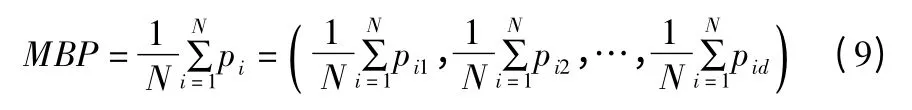
公式(9)中，MBP 是所有粒子个体最优位置的平均值.

所有粒子结合目标函数根据公式(10)和公式(11)在全局空间向最优位置移动.

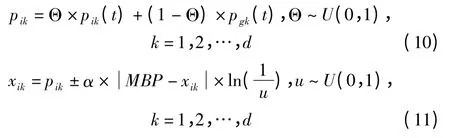
公式(11)中，0.5≤u＜1 时取减号，0＜u＜0.5 取加号.α是QPSO 的收缩扩张系数，本文采用α=((1－0.5)×(maxgeneration－generation))/(maxgeneration+0.5)，α 在算法收敛过程中线性减小.粒子在全局空间搜索的位置Xi由个体最优位置和种群最优位置计算得到.

模糊C 均值聚类算法就是将M 个观察值划分为C 类，记V=(v1，v2，…，vc)为C 个聚类的中心.每个观测值不是严格地划分为某一聚类，而是以隶属度划分，这里0≤uik≤1，且定义目标函数:

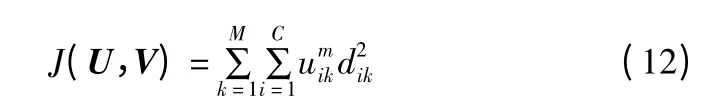
其中，m 一般取值为2.样本与聚类中心的距离公式:

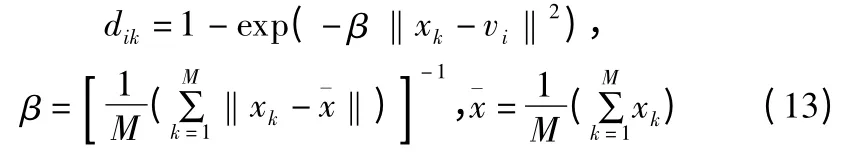
U=( uik)C×M为隶属度矩阵:

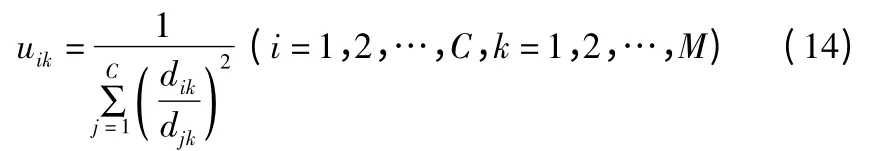
设定初始隶属度矩阵时，可以采用［0，1］上的随机数并做归一化处理作为每个隶属度的初值.计算得到样本集合的隶属度矩阵后，可以利用公式(15)得到新的聚类中心:

每个粒子的位置可以用向量 Xi=［vi1，vi2，…，vij，…，viC］表示，其中维数C 为设定的模糊聚类个数，vij表示第i 个粒子包含的第j 个聚类中心.在本文中，聚类中心为3 维向量，代表RSSI 三元组.每个粒子代表所有样本的一个候选聚类中心集合，最终得到的最优位置就是模糊C 均值聚类的最优全体聚类中心.基于量子粒子群优化的模糊C 均值聚类算法的聚类过程如下:

Step 1.设定粒子数N、粒子维数C、最大循环次数maxgeneration 和目标函数终止容限εJ，从样本集合随机抽取C个样本为每个粒子赋初值.

Step 2.初始化每个粒子的个体最优位置和粒子群的全局最优位置.

Step 3.根据公式(13)和公式(14)计算所有样本与粒子包含的每个聚类中心的距离和隶属度，按照隶属度最大值原则对样本进行模糊聚类.

Step 4.根据公式(15)计算新的聚类中心作为粒子的位置，并根据公式(12)计算粒子的适应度值.

Step 5.更新粒子的个体最优位置Pi和粒子群全局最优位置Pg，并利用公式(9)计算MBP 值.

Step 6.每个粒子依据公式(10)和公式(11)进行优化和移动自己的位置.

Step 7.循环Step 3 到Step 6，直到满足循环终止条件(循环次数=maxgeneration 或.得到最优聚类中心及相应模糊聚类结果.

由于聚类数C 值的选择对模糊C 均值聚类的效果影响很大，所以本文采用文献［22］的方法通过将模糊C 均值优化算法嵌入到遗传算法中迭代优化得到最优C 值及其对应的模糊聚类结果.具体步骤如下:

Step 4.利用公式(16)和公式(17)计算Cki的适应度值:

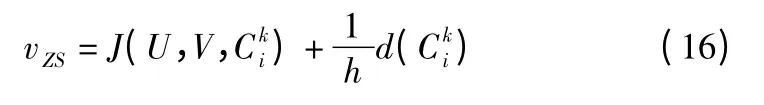
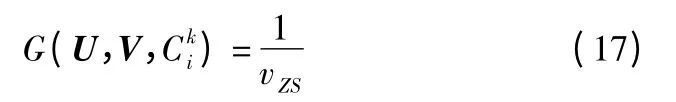
Step 6.判断是否达到遗传算法结束条件(达到最大进化代数或最优适应度值变化小于阈值):是，则结束，否，则到Step 7.

遗传算法收敛后，可以得到聚类数C 的最优值和最终的依据C 值得到的模糊C 均值聚类的分类结果.下一步将根据分类结果计算RSSI 的精确值.

设定水平置信λ，将模糊C 均值聚类相似矩阵转换为λ-Cut矩阵，将隶属度矩阵转化为布尔矩阵，根据布尔矩阵对RSSI 观测值三元组进行分类.由于RSSI 信号干扰是随机的小概率事件，所以选择元素最多的聚类作为标准聚类来计算RSSI 的精确值.但有时受环境或噪声影响，RSSI 信号分布比较分散，需要进一步判断所选择的标准聚类是否满足计算RSSI 精确值的条件.

本文采用假设检验的方法对标准聚类进行检验和判断，具体步骤如下:

假设Ai为标准聚类，为Ai的元素个数，分三种情况进行判断:

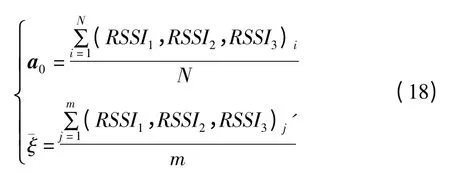
a0是整体RSSI 元组的平均值，ξ－是聚类Ai中RSSI 元组的平均值，根据假设检验原理，我们建立原假设H0:－ξ=a0和备选假设H1:ξ－≠a0.拒绝域如公式(19)所示:

定义α 为显著水平概率，我们得到公式(20):

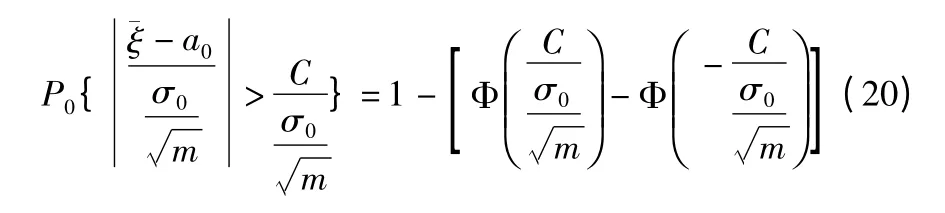
其中，δ0为标准聚类的均方差，)是期望为0，均方差为1 的标准正态分布函数，于是我们得到公式(21)和公式(22):

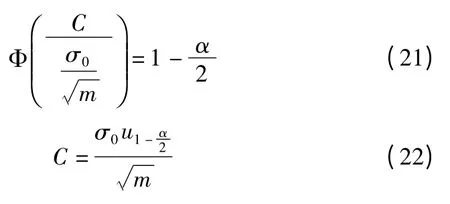
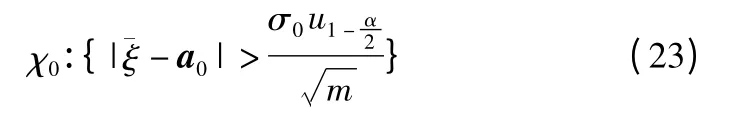
根据实际需要设定合适的显著水平概率 α(一般在0.05 ～0.1 之间)，然后计算标准聚类 Ai的 RSSI 三元组平均值.如果落在拒绝域χ0中，那么Ai将被放弃并要求锚节点重新发送RSSI 信号.如果 没有落在拒绝域χ0中，则标准聚类Ai可以用于计算RSSI 的精确值.确定使用标准聚类Ai后，根据模糊C 均值聚类算法得到的聚类中心，对RSSI 三元组进行加权计算.假设标准聚类Ai的聚类中心为vi:

Ai的RSSI 三元组所对应的矩阵为:

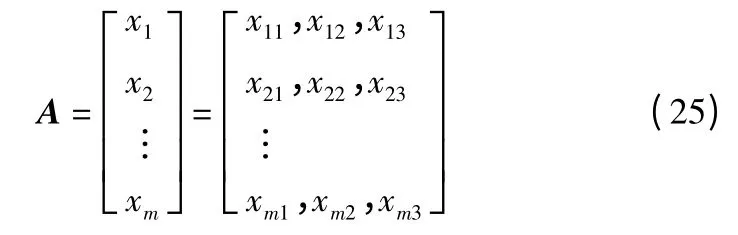
计算权值矩阵为:

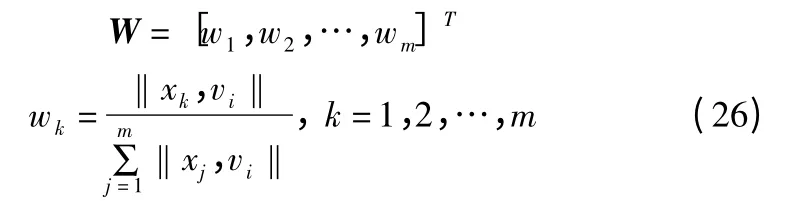
得到未知节点接收的RSSI 信号三元组为:

4.3 参考点加权质心定位算法

4.3.1 参考点加权质心算法原理

利用得到的RSSI 三元组可以计算三个锚节点到未知节点的距离，再根据三个距离计算得到三个参考点，并利用加权质心定位算法计算未知节点的坐标.参考点加权质心定位算法分为两步:

第1 步.计算三个参考点.

计算以锚节点M1为圆心，半径为d1的定位圆上的参考点 D1(xr1，yr1)，因为 D1(xr1，yr1)在以 M1为圆心且 d1为半径的圆周上，即:

D1(xr1，yr1)到其他两个锚节点M2，M3的距离:

D1(xr1，yr1)需要满足的参考点条件见公式(31):

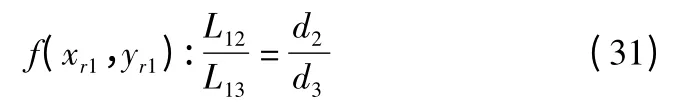
因为D1(xr1，yr1)应位于ΔM1M2M3内部，所以当参考点条件公式有多个解时，只保留位于ΔM1M2M3内部的解.可以通过两个锚节点确定一条直线方程，参考点和另一个锚节点位于该直线同侧的判定方法来得到符合条件的参考点.可以证明，在ΔM1M2M3内，满足条件的参考点D1(xr1，yr1)有且只有一个.

利用同样的方法，可以分别计算出M2为圆心d2为半径，M3为圆心 d3为半径上的参考点 D2(xr2，yr2)和 D3(xr3，yr3).

第2 步.加权质心定位.

根据加权质心定位算法计算未知节点的坐标:

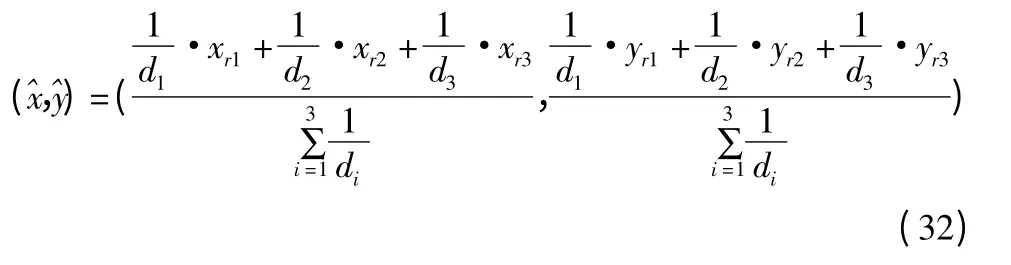
4.3.2 参考点加权质心定位算法的优点

优点1.传统的三边质心定位算法或加权质心定位算法需要以锚节点为圆心的三个定位圆两两相交，形成内侧3 个交点.但实际RSSI 测距过程中，由于信号脉冲噪声干扰、测距误差等原因，导致三个圆中只有两个圆相交甚至三个圆都不相交的情况，这个时候将无法利用定位圆的内侧交点对未知节点进行定位.如果此时利用三个锚节点的位置通过质心算法粗略计算未知节点的位置，将导致定位误差很大.本文提出的参考点加权质心定位算法则无论三个定位圆是否两两相交，即无论三个定位圆的位置如何，都能够计算出三个参考节点来对未知节点进行准确定位.

优点2.当三个定位圆两两相交时，计算的三个参考点在三个圆重叠部分的弧上，所组成的面积比传统三边质心定位算法使用的内侧交点形成的定位范围更小，因此对未知节点定位更准确，而且每个参考点在ΔM1M2M3内唯一.也可用同样的方法证明三个定位圆非两两相交时，三个参考点均在ΔM1M2M3内且唯一(证法同下).

证明三个参考点在三个定位圆重叠区域的弧上且唯一的过程:

如图3 所示，假设以M1为圆心d1为半径的定位圆周上的参考点A，经计算有:

假设A 点移动到D2时:

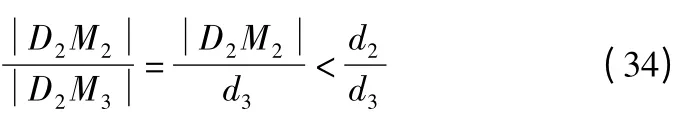
假设A 点移动到D3时:

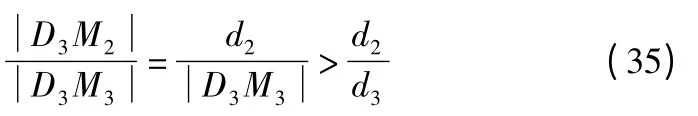
由于圆周外一点Q 与圆周中心M 的连线及延长线与该圆相交于两点N1，N2，其中为Q 到圆周的距离最小值点，为距离最大值点，且Q 与圆上其它点N 的连线距离随着N 沿着圆周轨迹运行过程中是单调递增或递减的(可以利用三角形三边法则或函数极值算法证明).所以P21为 A 到 M2的距离的最小值点，从P21顺时针移动到P31过程中，单调递增.P31为A到M3距离的最小值点，从P21顺时针移动到P31过程中，单调减小.所以弧D2D3(圆周上短弧，下同)上必有唯一一点A*满足:

当A 从D3顺时针移动到P31过程中，继续单调递增，继续单调减小.此时:

同理，当A 从D2逆时针向P21移动时:

所以在P21顺时针到P31这段弧上，满足参考点条件公式的A 点有且只有一个，且位于弧D2D3上.A 就是我们所求的以M1为圆心d1为半径定位圆上的参考点.同理可求得另外两个参考点，且这两个参考点位于弧D1D2和弧D1D3上.至此，ΔM1M2M3内唯一的三个参考点(xr1，yr1)，(xr2，yr2)，(xr3，yr3)已求得，且均位于区域SD1D2D3的三段弧上.证明毕.

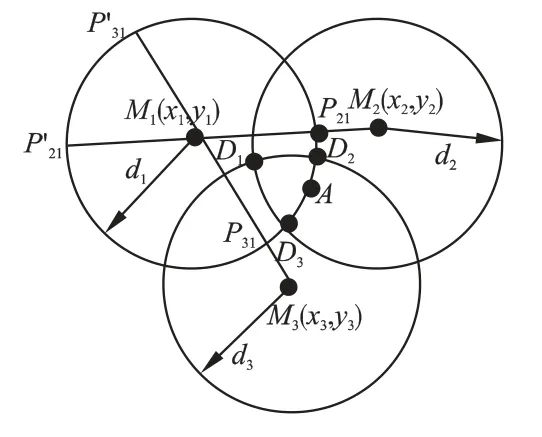
图3 参考点位置及唯一性证明Fig.3 Proof of reference node's position and uniqueness

5 实验仿真结果分析

5.1 仿真环境设置

仿真实验采用5 个CC2530 ZigBee 无线传输模块，其中一个作为未知节点，三个作为锚节点，一个作为网关通过RS232 串口线与上位机相连.未知节点、锚节点和网关节点采用TinyOS2 开发环境和Keil 编译器编写应用程序实现功能.三个锚节点向未知节点发送RSSI 信号，未知节点接收RSSI信号并存储在寄存器中，再通过网关传输到上位机中利用定位算法对未知节点进行定位.RSSI 信号的噪声模拟采用信噪比为－5，标准峰值为1 的随机信号以一定概率γ 加载在RSSI 信号上生成噪声信号.计算结果采用100 次测试数据的平均值.

采用定位误差率判断定位算法性能，即定位结果的绝对误差与节点通信半径的比值:

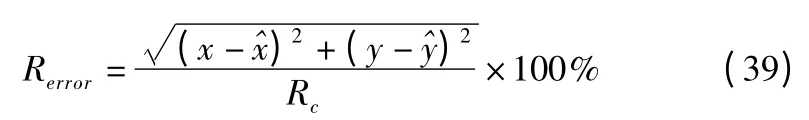
RSSI 测距误差率由公式(40)计算，其中 dm为 RSSI 测距，d^ 为未知节点与锚节点的真实距离:

5.2 仿真结果分析

如图4 所示，当未知节点和三个锚节点的距离相同的情况下(设置均为10m)，每个锚节点每次向未知节点发射500个RSSI 信号，可组成500 个RSSI 信号观测三元组.为验证遗传算法是否得到了模糊聚类最优C 值，仿真对最优C 值及邻近值对应的模糊聚类计算的RSSI 测距平均误差率进行了对比和分析.模糊C 均值聚类的C 值取值不同，对应的聚类结果及RSSI 测距误差也不一样.当C 值小于最优值时，无法对RSSI 的干扰信号进行有效排除，所以导致测距误差率较大.当C 值在最优值附近时，RSSI 测距误差率相差不大，但超过这个范围，误差率显著增加.当C 值过大时，RSSI 测距误差率产生了波动.这是因为当聚类数较多时，由于标准聚类的RSSI 样本数量较少导致聚类中心偏移而使得测距误差率增大并产生波动.所以本文采用遗传优化算法可以得到模糊C 均值聚类数的最优值.

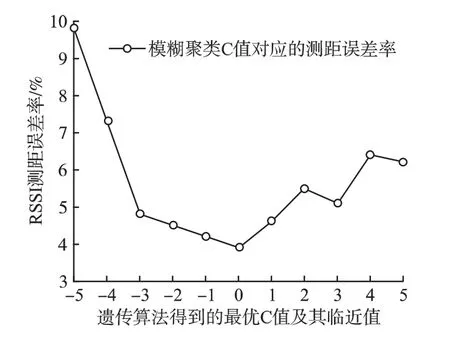
图4 聚类个数对RSSI 测距的误差的影响Fig.4 Influence of C value on RSSI ranging error

如图5 所示，当未知节点和锚节点距离较小时(例如5m)，基于RSSI 的平均值法和本文提出的模糊C 均值聚类法的测距误差率相差不大.但随着距离的增加，平均值法从10m开始误差率就快速上升，而模糊C 均值聚类法的误差率上升较慢，大约25m 起误差率上升略有加快.说明模糊C 均值聚类法可以有效地消除小概率大干扰噪声信号对RSSI 测距造成的影响.随着距离的增加，两种算法的误差率差距逐渐增大，当距离为40m 时相差13 个百分点.如表2 所示，当三个锚节点在10m 处发射100 次RSSI进行定位，在可视距内设置相同障碍物的前提下，在不同噪声概率γ 下，统计成功定位次数和定位误差率.传统三边质心算法由于三个定位圆不满足定位条件而出现无法对未知节点定位的情形，而且随着噪声概率γ 的增大，定位失败的次数不断增多.但改进的算法利用参考点加权质心算法成功地进行100 次定位，而且定位误差率更低.这说明本文提出的改进算法的可靠性更好，定位精度更高.

图5 两种方法的RSSI 测距误差率比较Fig.5 Comparison of RSSI ranging error rate

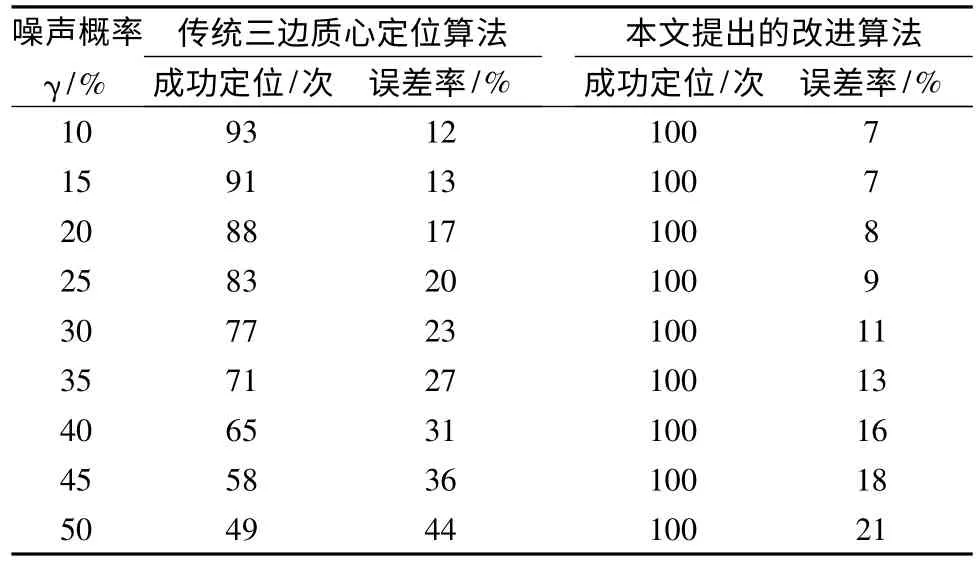
表2 定位性能比较Table 2 Comparison of localization performance

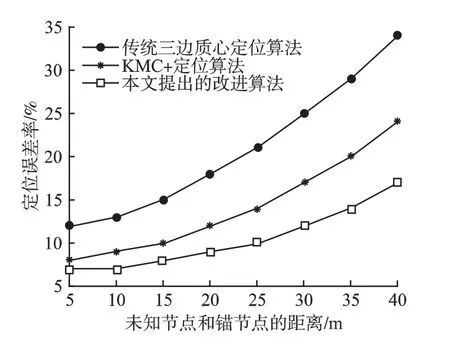
图6 三种算法的定位误差率比较Fig.6 Comparison of localization error rate of three algorithms

如图6 所示，在噪声和障碍物因素相同情况下，对传统三边质心算法、文献［7］提出的聚类改进KMC+算法和本文提出的改进算法的定位误差率进行了比较.三种算法定位误差率都随着未知节点和三个锚节点的距离增加而增大，但本文提出的改进算法的定位误差率增加的最小.随着距离的增加，RSSI 测距误差也随之增大，传统三边质心算法无法有效消除误差而导致定位误差率快速上升.而KMC+算法虽然对定位结果进行了聚类，但在基于RSSI 源数据处理和对每个聚类中心计算平均值进行定位过程中，无法有效消除小概率大干扰因素的影响，所以误差率也随距离的增加而较快上升.本文提出的基于量子粒子群优化的模糊C 均值聚类算法因为具有全局搜索能力，所以避免了局部极值解的出现，最终收敛于最优解.通过记录历史全局最优解，与最后得到的最优解进行比较来做出最终选择，可以有效防止优化算法在最优解附近的抖动现象，进而可以计算得到RSSI 的准确值并提高定位精度.本文提出的改进算法与传统三边质心算法和KMC+算法在距离40m 内的定位误差率平均相差10 个和4 个百分点，当间距为40m 时，分别相差17 个和7 个百分点.这说明改进算法通过得到相对准确的RSSI 值计算的未知节点和锚节点的距离更贴近真实值，再利用参考点加权质心算法减小定位区域，有效减小定位误差率并提高定位精度.

6 结 论

节点定位技术是无线传感器网络的研究重点之一.本文针对传统三边质心定位算法定位精度较低的缺点，提出了基于模糊C 均值聚类的参考点加权质心算法.仿真结果表明，改进算法的RSSI 测距误差更小，定位精度更高，弥补了传统三边质心定位算法的不足.此外，改进算法没有更多硬件需求，只是在原有算法的基础上增加了一些计算量，能较好地适应WSN 低成本与低功耗的要求，是一种较优的三边定位方案.虽然三边定位算法简单，对硬件要求小，且易于部署和应用，但该算法对每一个锚节点的依赖度很高，如果其中一个锚节点失效，将对定位精度造成极大影响，所以如何识别失效锚节点并有效对定位结果进行修正和优化将是今后研究的重点.