基于判决HMM和改进Viterbi的钢琴指法自动标注方法

李 锵，李晨曦，关 欣

基于判决HMM和改进Viterbi的钢琴指法自动标注方法

李 锵，李晨曦，关 欣

(天津大学微电子学院，天津 300072)

现有的一阶隐马尔可夫模型(hidden Markov model，HMM)用于钢琴指法标注不能结合音符序列的长程信息，导致标注结果存在物理不可弹指法，且演奏效率较低，因此本文提出了一种基于判决隐马尔可夫模型和改进维特比算法的钢琴指法自动标注算法．结合指法规则的先验知识，在HMM中引入了判决函数，从而能够去除错误的穿跨指和超出可弹跨度的指法．在预测指法路径时，改进了维特比算法的寻优规则，首先根据先验知识对音符序列进行八度分段，并改进初始指法的确定方法，最后选择穿跨指数最少、演奏效率最高的指法序列为最优指法．为了表征算法的性能，文中还提出了不可弹指法占比率和欠合理率两种新的评价指标来衡量指法的可弹性和演奏效率．通过实验验证，文中算法相较于现有标注模型在一致率和两种新的指标上提升效果显著．另外，为了对比在小数据集下传统方法和深度学习方法的性能，还与Bi-LSTM＋CRF进行了对比实验，训练时分别采用原始音符序列和音符差分序列，实验结果显示利用音符差分序列可以有效提高标注结果的一致率，由此可见，相较于原始音符序列，指法标注和音符差分序列的关系更密切，从而进一步验证了本文算法结合音符差分信息改进HMM的有效性．但现有数据量下，深度学习模型在不可弹指法率和欠合理率上差于本文算法．

钢琴指法；判决隐马尔可夫模型；先验知识；改进维特比算法

指法是钢琴演奏中最基本最重要的技术之一.合理的指法即手指的运动规律满足以下两点：①符合手的生理结构及每个手指的灵活性等特点；②满足手指与音符间的关系．合适的指法可以增加演奏的流畅性，这对快板(allegro)类乐曲尤为重要．理论上每个钢琴谱都存在最佳指法序列，但目前要确定乐谱的理想指法主要依赖经验反复尝试．因此钢琴乐谱自动指法标注可以节省实践时的探索时间，消除业余爱好者早期的演奏障碍，并为职业钢琴家提供初始参考指法．如果将该任务看成钢琴演奏机器人运动规划的一部分，实现指法自动标注的方法还能推广至使用类人机器手的更一般的机器人操作任务中．

目前，钢琴指法自动标注方法主要有两类：基于规则的方法和基于统计学习的方法．文献[1-9]中将指法规则和动态规划相结合进行标注．Parncutt等[1]在1997年设计了第1个钢琴指法的计算模型．研究人员将指法标注任务分为短序列和长序列部分．对于短序列，模型按照特定规则对所有可能的指法进行评估并排序；对于长序列，定义指法成本的计算方法，采用传统的动态规划方法寻找指法成本最低的路径．该模型后来由Jacobs等[2]进行了改进，修改了启发式算法，并用物理距离替换了原始模型中不精确的半音测量．Hart等[3]描述了一种简化的但更个性化的方法．Kasimi等[4-5]定义的指法成本包括对旋律(melodic)的水平测量以及和声(harmonic)的垂直测量，然后使用网格图来代替音乐片段寻找代价最小的路径．Nellåker等[6]引入更多的规则来评估指法序列. Lin等[7]设计了一种基于图形的指法生成器(slicing fingering generation，SFG)，它可以实时生成MIDI音符的钢琴指法，该算法分为两层，上层的音符处理器检查输入的MIDI音符并控制指法生成的进度，下层的指法生成层采用动态规划的思想生成指法．

Viana等[8]描述了一种混合方法．首先，“专家系统”采用指法中最常见的规则进行编码，当没有规则适用时，转为遗传算法．其中待弹奏的音符序列对应遗传算法中的染色体，最大化适应度函数(fitness function)的过程变为最小化“指法距离”函数．基于规则的方法最普遍的问题是需要处理指法中多个适用规则之间潜在的矛盾冲突，难以为各种规则设计一个合理的权重来衡量不同规则在指法确定过程中的重要性．

基于统计学习的方法中，Yonebayashi等[9]使用HMM为指法序列建模，音符对应的手指序号为待预测的指法状态，每个指法状态出现的概率取决于前一时刻指法状态和当前时刻的音符输出．笔者人为估计转移概率参数，并使用维特比算法计算概率最大的指法状态序列．但一阶HMM的两个假设导致指法标注没有结合相邻音符的信息，标注结果会出现不可弹的指法转换，并且该模型只用于单音序列，不包括和弦．之后Nakamura等[10]提出“合并的HMM”对未分离左右手声部的乐谱进行自动分离和标注，模型使用两个并行的HMM，将两者的输出合并，但效果提升不显著．Sun等[11]扩展一阶HMM的参数实现了对乐谱中和弦的标注．除钢琴指法外，HMM也用于搜索最优的吉他指法[12-14]．Hori等采用常规的HMM建模和解码方法研究吉他指法标注，之后结合实际弹奏的经验，在预测指法阶段提出了最小化最大动作难度的极小极大化维特比算法(minimax viterbi algo-rithm)[13]和维特比算法参数化系列Lp-Viterbi[14]．

除了基于规则和统计学习的方法外，钢琴指法标注类似于自然语言处理的时间序列标注问题，近些年来深度学习在该领域成果显著，如在词性标注问题中，使用双向长短时记忆网络(bidirectional long-short-term memory)与条件随机场(conditional random field)相结合(Bi-LSTM＋CRF)[15]，将LSTM的输出作为状态特征函数，极大化真实标签序列的得分，取得了目前为止最好的结果．LSTM对时间序列具有长距离记忆性，并且可以自动调整记忆长度，丢掉冗余信息，利用强相关时刻的信息进行预测，Bi-LSTM还可以同时兼顾向前和向后两个方向的上下文信息，理论上同样适用于钢琴指法标注这种需要利用长度不一的上下文音符信息和指法信息进行预测的问题．将Bi-LSTM每个时刻的输出作为CRF的状态特征函数得到全局最优解．但由于深度学习不便于加入先验知识，完全依赖大量神经网络参数的非线性拟合，需要海量、完备的训练数据集来保证泛化能力．对于钢琴指法问题来说，目前尚缺少公开数据集，数据数量有限，这种条件下，本文侧重于对现有的统计学习方法进行改进．

有监督训练的HMM学习了两指之间转换的概率信息和指号到音符间一一映射的概率信息，由于现有的一阶HMM的齐次马尔可夫性假设指法间的依赖时长只有一个时刻，不考虑长距离信息，导致标注结果中穿跨指较多，手位更换频繁，影响演奏效率；观测独立性假设音符间相互独立，指法确定时不考虑其他时刻音符信息，导致出现了不符合手指运动规律的不可弹指法．针对上述问题，笔者结合钢琴指法的先验知识提出了判决HMM和改进的维特比算法：首先在模型构建时将转移概率改进为判决转移概率，加入音符差分信息修剪不可弹的指法路径；然后在预测时，将相邻音程超过一个八度的前后音符序列分段标注，目的是避免局部路径被修剪后无可选指法路径的情况，标注无法继续进行；接着修改维特比算法的预测规则，即笔者人为设定初始时刻指法状态，并且在以不同状态结束的最大概率路径中，选择演奏效率最高的路径为最优指法路径，此外，还提出了错误指法占比和欠合理率两个指标衡量标注结果，并在本文的数据集上对比其他现有算法；最后，通过一定量数据集的实验验证，相较现有标注指法算法，性能有了较大的提升，一致率可以达到66.45%，错误指法占比降为0，所提出的欠合理率折中地评价了演奏效率和舒适度，算法标注结果的欠合理率由17.20%降低至1.84%.另外，为了对比在小规模训练数据下本文算法与深度学习模型的性能，笔者使用同样的数据集在Bi-LSTM＋CRF模型上进行了训练和预测，一致率仅有55.06%，错误指法占比为15.92%，不可弹指法为16.30%，原因是音符到指法的一对多映射种类过多，数据集可覆盖的映射种类太少，网络参数拟合难度太大．因此将原始音符序列修改为音符差分序列进行训练，音符差分映射到指法种类数大大减少，一致率可以达到67.90%，错误指法占比为3.00%，不可弹指法占比为5.02%．在当前数据集数量的约束下，Bi-LSTM＋CRF在一致率上稍好于传统方法，但从演奏的可弹性和效率来说，本文的算法优于深度学习模型.

1 自动指法标注模型

现有方法的指法标注结果存在3个问题：一是局部出现了错误的穿跨指；二是出现超出手指间最大跨度的指法；三是整体弹奏效率不高．针对上述问题，笔者利用指法规则先验知识改进了HMM模型和预测指法状态的方法，整个指法标注模型的原理框图如图1所示．将钢琴指法的先验知识与隐马尔可夫模型相结合，利用先验知识，在训练阶段将模型参数转移概率改进为判决转移概率，使得预测时的不可弹指法路径被修剪；预测时加入八度分段将待标注的音符序列分割成子序列进行分段标注，并改进了维特比算法的初始状态确定方法和寻优策略．

第1.1节介绍了常用的指法设计规则，包括正误穿跨指、可接受的最大音程跨度、手部移位准则和初始指法确定规则．第1.2节提出判决隐马尔可夫模型．第1.3节介绍模型的参数估计．第1.4节介绍指法序列的预测阶段．

图1 利用指法先验知识的改进HMM方法原理

1.1 指法规则先验知识

1.1.1 正确指法转移类型集合

钢琴乐谱中的音符序列由单音与和弦构成．单音符序列基本指法包括顺指、穿指、跨指、扩指、缩指．顺指法即在自然手位下，一个手指弹奏一个音符，它是演奏中最常用的基本指法．穿指和跨指即“拇指潜移”和“穿跨拇指”，分别指将1指(拇指)从2、3、4指下面穿过和将2、3、4指从1指上面越过，其他手指间的穿跨不被允许，穿跨指主要发生在连续的音符上升或下降时，作为手位移动处的衔接．扩指和缩指即手指的横向张开和横向紧缩，发生在两个指号差小于或大于音符间音程时．和弦指法是同一时刻发生的顺指或扩指．

上述5种基本指法包括了所有允许的手指转移组合，其中穿跨指对指号有要求，因此5×5个手指转移组合不全是任意可行的．以右手为例，音符升时，2、3、4指转移到1指是正确穿指，其他指号降的情况为错误穿跨指，如图2(a)中1指(拇指)从5指(小指)下穿过，即5指转移到1指为错误穿指；图2(b)中4指从5指上的跨过，即5指转移4指为错误跨指；音符降时，1指转移到2、3、4指是正确跨指，其余指号升的情况为错误穿跨指，左手情况与上述相反．

表1总结了右手音符降(与左手音符升时情况一致)的正误指法转移组合，右手音符升(左手音符降)时的正误指法转移情况与表1斜对角镜像对称．笔者利用这一先验知识保证指法的正确性．

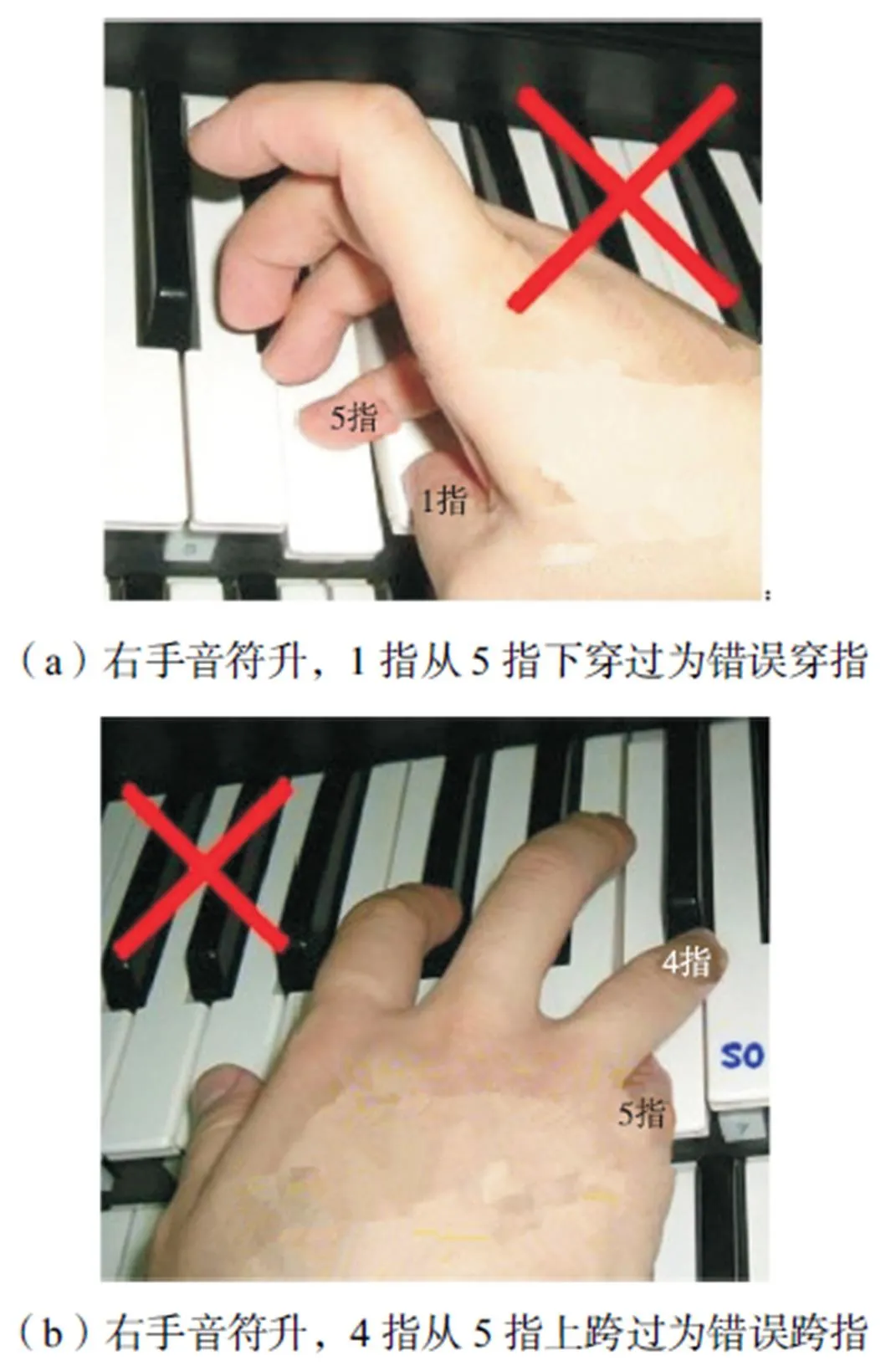
图2 右手错误穿跨指示意

表1 左手音符升/右手音符降的正误指法

Tab.1 Left-handed note up/right-handed note drop posi-tive and false fingering

1.1.2 音程约束先验

合适的指法还需要两指间具有可承受的音程跨度，Parncutt等总结了任意两指在轻松、舒适和可实现3种弹奏状态下可跨越的最大音程差，详见表2[1].笔者选取舒适状态下的最大音程差MaxComf约束可转移的手指选项，超出MaxComf音程跨度的指法组合均视为很吃力的指法，尽量不被使用，最坏情况下不能超过MaxPrac．

表2 两指在轻松、舒适和可实现状态下的最大音程差

Tab.2 Maximum span of the two fingers in a relaxed，comfortable，and practical state

1.1.3 手部移位先验

穿指、跨指、扩指和缩指都发生了手的移位，一般将穿、跨指导致的移位归为穿跨式移位，扩指和缩指归为伸缩式移位．还有一种平移式移位，发生在相邻音符音程差太大，超出了当前手位下1、5指可及的最远距离，即使加入穿跨指小范围地扩张可弹跨度也无法继续的情况．平移式移位切断了前后指法的关联性，移位后从头开始安排后续指法．

对整首乐谱指法来说，简易自然是良好指法的基本原则，手部移位容易造成演奏的不连贯．必要时手部移位的原则是移动后能在新位置上以自然手位弹奏尽可能多的音符，尽可能减少移位次数，提高演奏效率．原则上能用伸缩式就不用穿跨式，平移式在相邻音程差超过八度时加入．在一首乐谱所有正确、可弹的指法序列中，穿跨式移位最少的指法序列演奏效率最高．平移式移位切断了前后指法间的相关性，此时整个乐谱指法序列标注问题转化为对子序列的指法标注．

1.1.4 初始指法先验

每一段标注的初始时刻指法会影响整段指法的后续安排，人工标注指法时往往先根据前几个音符的指位先后确定第1个时刻指法，再进行后续标注．为了接近人工标注的思路，从而提高与人工标注结果的一致率，笔者不利用最大化指法序列概率的方法回溯初始时刻指法，而是依据初始音符在前5个不同音中的音高所处位置，选择使前5个音都能以自然手位弹奏的指号作为初始指法．

1.2 判决隐马尔可夫模型

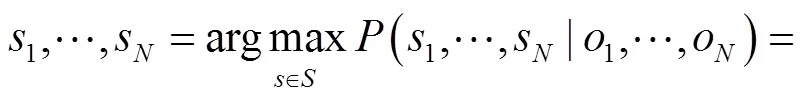
由一阶HMM的齐次马尔可夫假设和观测独立性假设得出

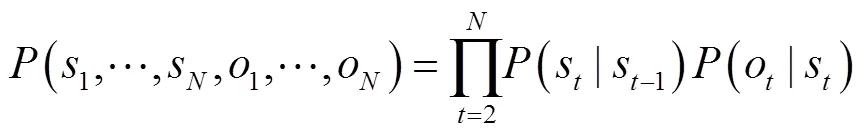
给定音符序列时分母不变，因此HMM的预测目标变为

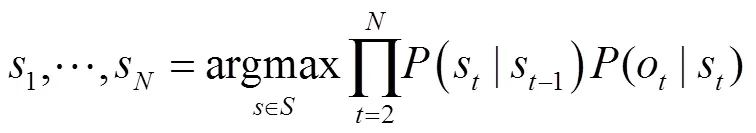
为了在计算指法转移概率时兼顾相邻时刻的音符信息，避免不可弹指法的出现，将指法转移概率改进为当前音符和前一音符下的条件转移概率，即

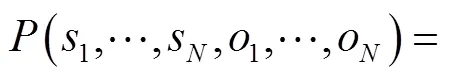
则预测目标改进为

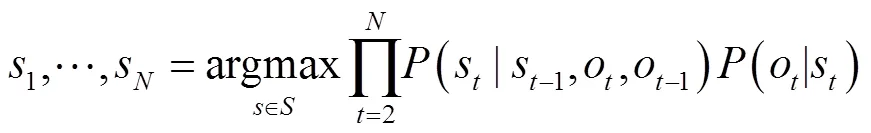
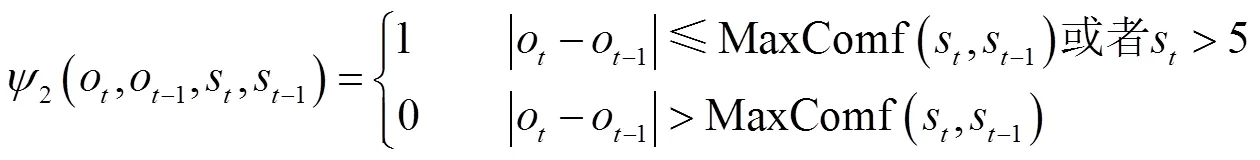
预测目标变成

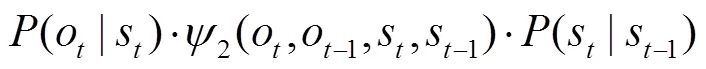
1.3 参数估计

参数学习采用有监督的方法，利用极大似然法估计状态转移概率和音符观测概率．模型不仅处理单音序列也处理含有多音和弦的序列，单音种数即钢琴琴键数88，多音和弦考虑在一个八度内的二音至五音和弦，共计61841种．指法状态包括5种单指状态和26种多指状态．

1.4 预测最优指法序列

1.4.1 音符序列分段预处理

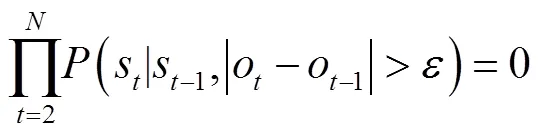
此时对整个音符序列搜索指法路径，会导致

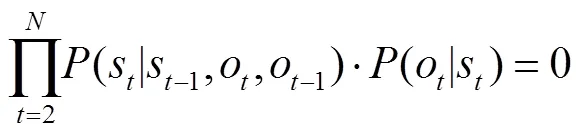
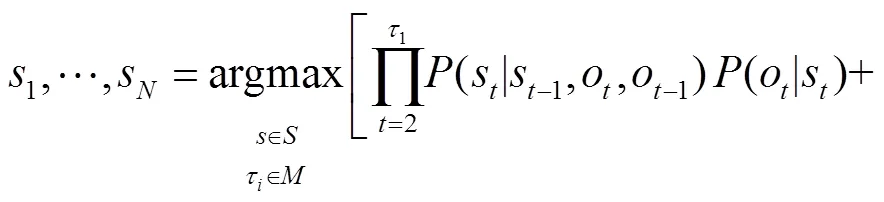
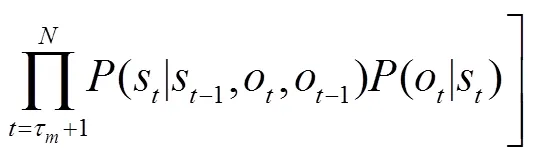
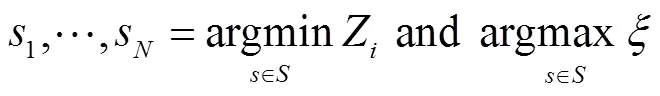
1.4.2 初始时刻指法

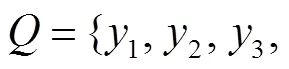
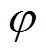
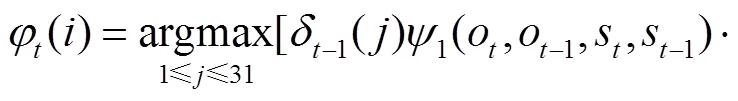
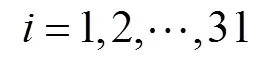
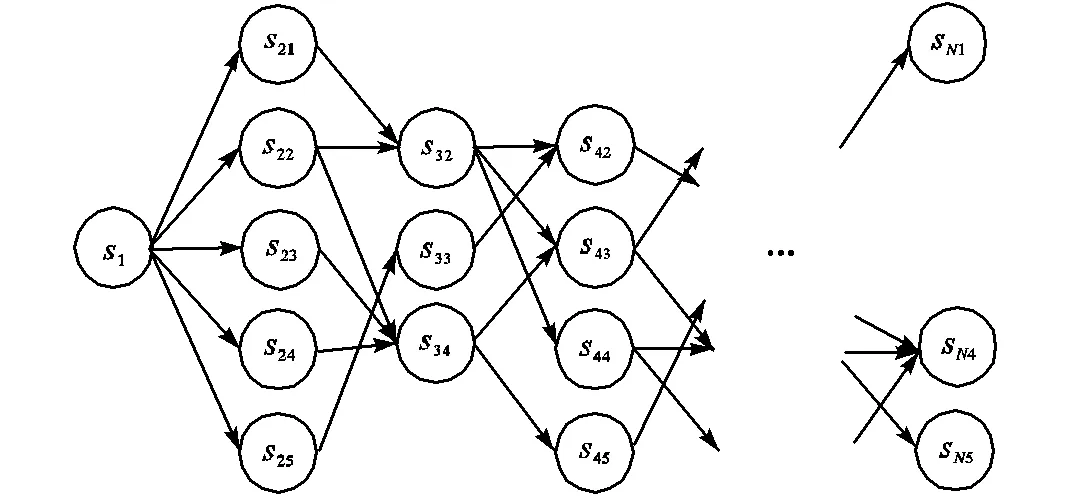
图3 初始状态受限时维特比算法路径搜索示意

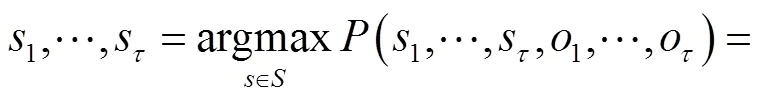
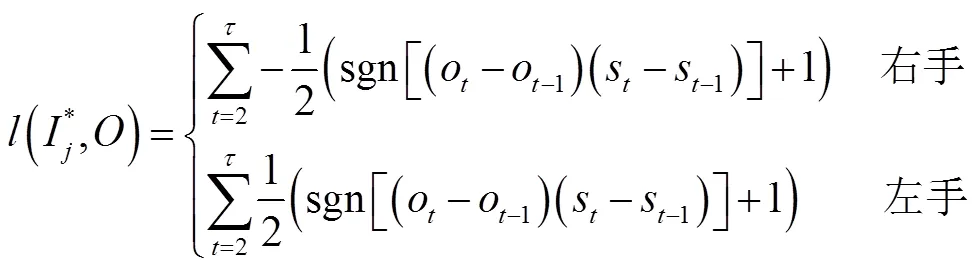
2 实验结果及分析

2.1 数据集

目前尚未有正式公认的数据集及评测指标，故自建了数据集，采用了Bach 28短篇钢琴(28首)，Cherny 299(5首)和中国音乐学院社会艺术水平考级1～3级(7首)，共计40首，左手4000多音符，右手6000多音符．为了验证模型的可靠性，笔者将数据集分为5组，进行五折交叉验证，并且设计了8组实验来对比验证笔者方案的改进之处．

2.2 数据集的特征及参数选择

88个音符输出的组合数十分庞大，输出概率矩阵中的参数将达到31×61929≈190×104，其中4音和弦、5音和弦的组合数目占到了89.8%．对数据集中的音符和指法进行统计，4音和弦和5音和弦出现的概率极低，近似为0，因此笔者删掉输出概率矩阵和转移概率矩阵中的4音、5音和弦音符和指法，输出概率矩阵缩减为(88＋978＋5236)×25≈16×104，条件状态转移矩阵为25×25＝625．在单音和2、3指和弦组成的输出概率参数矩阵中，2指、3指和弦占到98.6%，然而如图4所示，笔者的数据集中多指和弦十分低频，且很多位置频次为0，原因是笔者的模型效果更关注对手指转换要求更高的单音序列乐谱，因此训练集中和弦覆盖不多，后续需要加入更多带有和弦的数据集．

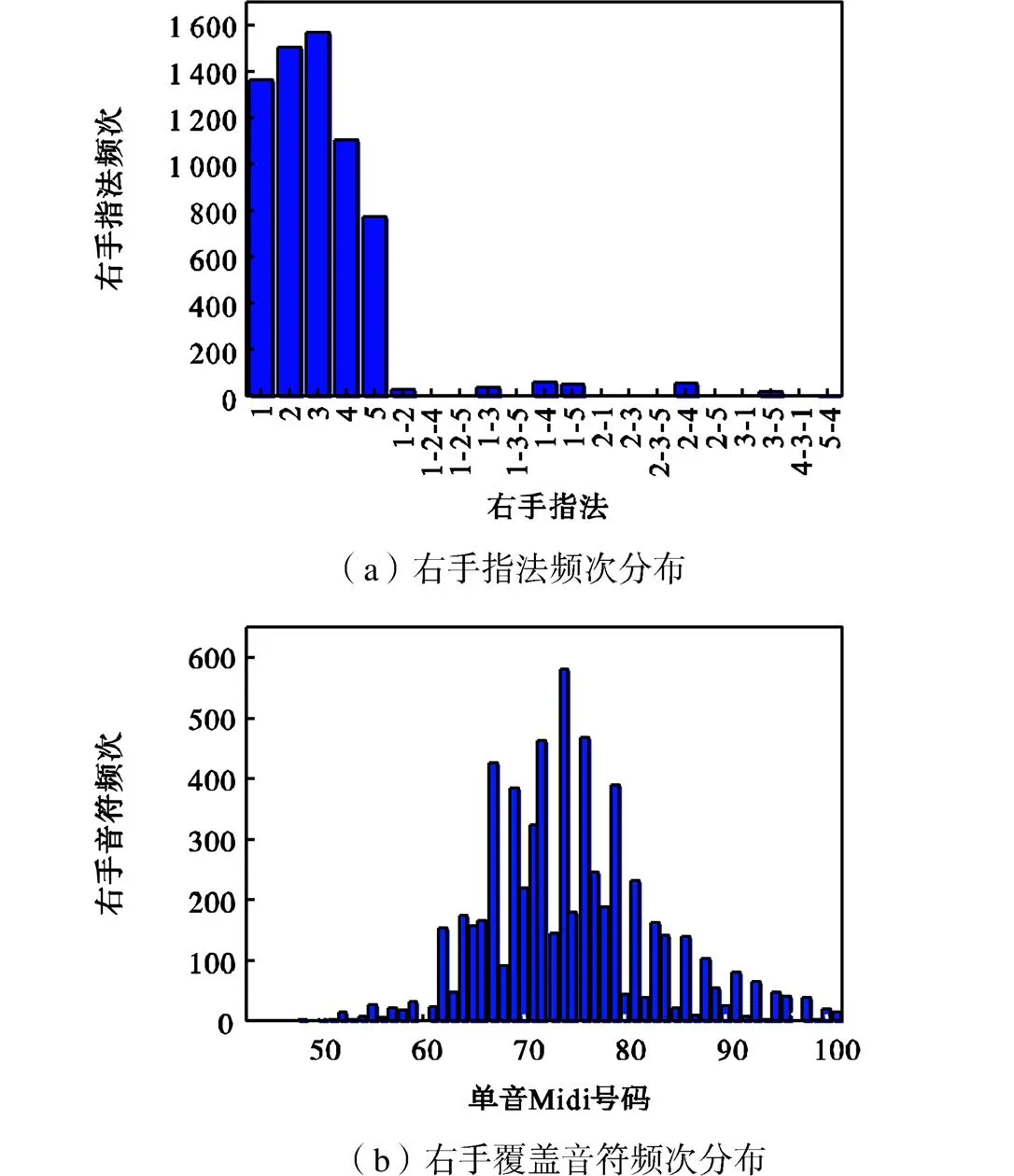
图4 右手音符和指法频次分布

输出矩阵理论上遍布了所有音符，但如图4所示，右手覆盖的音符Midi号范围(21～108)主要集中在右半区，左手同样集中在左半区，极少数会出现在另半边区域，因此左右手模型的输出概率矩阵待训练参数又缩减一半．

2.3 评价标准

2.3.1 一致率

但指法问题的特殊性在于标注具有时间传递性和多态性．时间传递性即每个时刻指法的选择会影响后续时刻，若某一时刻标注结果与标签不一致，会导致后续一段时间的标注大概率与标签不一致，一致率显著降低；多态性即指法有时会有多种选择，如1-3指和1-2指均可的情况并不少见，人工标注在面临这种选择时具有一定的随机性，没有严格的挑选标准．若算法在多种可选项中选择了与人工标注不一致的情况，会导致后续一段时间的标注结果和标签产生一个手指的错位，大大降低一致率，但实际演奏时，指法连续错位一指仍然有可能是可以弹奏的指法序列，因此一致率并不能完全反映标注的质量．

2.3.2 不可弹指法占比率

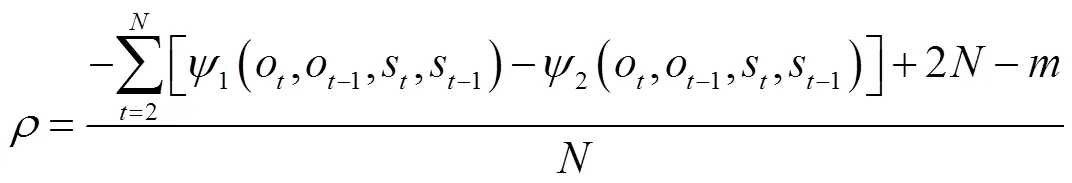
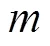
2.3.3 欠合理率

2.4 结果及分析

为了验证判决函数、八度分段和改进维特比算法对标注结果的影响，本文设计了6组对比实验和5组现有算法对比实验，每组实验进行了五折交叉验证．其中在判决HMM的预测阶段，由于判决函数修剪了大量路径，不分段处理会产生下一时刻没有可选指法的情况，因此判决HMM+Viterbi和判决HMM+改进Viterbi的实验可用数据相较其他组有所减少，无法对比评价，如相邻小节的音符差超出了一个八度，不进行分段处理找不到合适的衔接指法，因此该种组合未加入对比实验．另外，有无判决函数的HMM参数不同，导致维特比算法的中间概率计算方法不同，对维特比算法的改进指初始状态和最优路径的确定方法两个改进之处．5组现有算法的对比实验包括对Original HMM、Fault-tolerant HMM、Merged-output HMM、LSTM＋CRF 4种训练模型和本文的Judgement-HMM，前4种模型均采用原始Viterbi算法进行预测，判决HMM采用改进Viterbi进行预测．

2.4.1 对比实验

为了验证不同改进点的作用，笔者设计了6组对比实验，结果如图5所示．A为HMM＋Viterbi，B为HMM＋八度分段＋Viterbi，C为HMM＋改进Viterbi，D为HMM＋八度分段＋改进Viterbi，E为判决HMM＋八度分段＋Viterbi，F为判决HMM＋八度分段＋改进Viterbi．传统HMM下，分别加入八度分段和使用改进维特比算法相较传统维特比算法，标注结果一致率提升了0.15%和4.37%，不可弹指法占比率分别下降0.08%和1.30%，欠合理率分别下降0.15%和0.25%；将二者联合使用一致率提升4.43%，不可弹指法占比降低1.56%，欠合理率下降5.10%.由此可见，改进维特比算法较明显地提升了标注的一致率，八度分段提升不明显，但二者结合后，欠合理率下降明显，原因是分段后对每段子序列搜索演奏效率最高的指法再进行组合，比整体搜索的可选路径更多，效果更好．判决HMM和八度分段联合使用时，相较传统HMM和八度分段一致率提升9.16%，原因是判决函数修剪了错误的穿跨指和超出音程跨度的指法路径，大大缩小了指法搜索空间，使标注结果更大概率接近人工标注结果，而不可弹指法占比率则从23.50%直接减为0，指法序列完全物理可实现．再加上对维特比算法预测阶段的改进，相较未改进前一致率提升5.57%，欠合理率下降至1.84%，很接近人工标注设定的穿跨指数．

图5 对比实验结果

为了具体说明改进点对指法的益处及本文算法标注结果的性能，并验证一致率指标的缺陷，截取了实验的部分标注结果，如图6～图8所示．图6为Bach 28首短篇钢琴中Minuet in G major高声部(右手)两小节标注结果，图6(a)、(b)、(c)分别为Groundtruth、传统HMM＋Viterbi和判决HMM＋改进Viterbi的标注结果．图6(b)中传统HMM＋Viterbi标注的5指-3指跨越了G4到G5，即一个八度，在不变换手位的情况下，超出了表2中3指到5指间的最大可弹奏跨度，属于超出可弹跨度的不可弹指法，且第2小节的4指-3指为错误的穿跨指，而图6(c)中第2小节3指-2指-1指相较(a)中的4指-3指-2指发生了连续1指的错位，从表面上看，图6(b)、(c)都与Groundtruth不一致，但显然图6(c)中的标注结果要较图6(b)更合理，图6(b)中第2小节甚至还存在1-3的跨指.在第2小节的标注结果中，图6(b)有3/5的指法与Groundtruth一致，图6(c)只有2/5的指法与Groundtruth一致，但是在容错范围内图6(c)更合理，可以看出，一致率不能完全衡量指法标注算法的性能．此外，还可以发现，传统HMM+Viterbi中不一致指法的前后相关性不强，而判决HMM＋改进Viterbi则容易出现一连串与Ground-truth不一致的标注结果，这将更容易降低一致率．相对而言，判决HMM＋改进Viterbi容易出现一致率极高或极低两种极端情况，在测试集中，最高可高达85%，最低则仅有45%．

图6 《G大调小步舞曲》高声部指法的改进算法前后结果对比

图7体现了本文算法去除了超出手指音程跨度的错误指法．图7为中国音乐学院考级三级B组《小草》片段低声部的两小节标注结果，第1小节最后一个音符F4到第2小节第一个音符B2超出了一个八度，图7(a)中在此处进行了八度分段，否则会出现在第1小节结束后找不到可转移指法，之后标注时将每一段指法约束在可弹音程范围内；图7(b)中未加音程约束，使得出现大量超出音程跨度的指法，如图中5指-4指演奏(MIDI号50)-A3(MIDI号57)的MIDI跨度为7，而表2中4-5指间MaxPrac仅为5，同样地，4指-3指演奏B3-(MIDI号46)-A3(MIDI号57)的MIDI跨度为11，而表2中3-4指间的MaxPrac仅为4，这两处均为超出了手指最大跨度的不可弹指法；反观图7(c)中加入音程约束后，由于修剪掉大量不可弹的选项，每一小节较为容易地实现了和Groudtruth一样的标注结果．并且在两小节切换处，由于音程超出了一个八度，两个结点F4-B2的指法并不具有任何相关性，在Viterbi倒序确定F4指法时并不应该参考B2的指法，图7(b)中这一过程是无效的标注．图7(c)中加入的八度分段结合音程约束符合人工标注的思路，有效实现了一致率的提升．

图7 《小草》低音部指法的改进算法前后结果对比

为了表征算法对和弦序列的标注性能，图8截取了中国音乐学院考级1级自选曲目《卖报歌》低声部片段的和弦标注指法．由于训练集中和弦的数据量很稀疏，基本上一种和弦对应着一种概率为1的指法．因此在标注时，训练集中出现过的和弦可以正确标注，如图8中的和弦标注所示．但还有大量和弦在训练集中未覆盖，为了避免未出现过的和弦所有输出概率为0，导致无法标注，将该类输出概率均设为4%，因此和弦的数据集不足也一定程度地导致了标注结果的一致率低．

图8 本文算法和弦标注指法结果

2.4.2 不同算法性能对比

将本文算法与现有的钢琴指法自动标注算法在相同数据集上做了对比，结果如表3所示，相较现有基于HMM的标注算法，本文的改进在3项指标上都取得了较大的提升，Fault-tolerant HMM[11]在评价标注结果时虽然考虑了指法的容错性，使得指法的一致率有所提高，但没有关注标注结果中的不可弹指法；而Merged-output HMM[10]在训练输出概率和转移概率时从空间上加入了轴对称的限制，弥补数据的缺失导致的低一致率，但也没有考虑标注结果中的不可弹指法．

表3 不同算法的标注结果对比

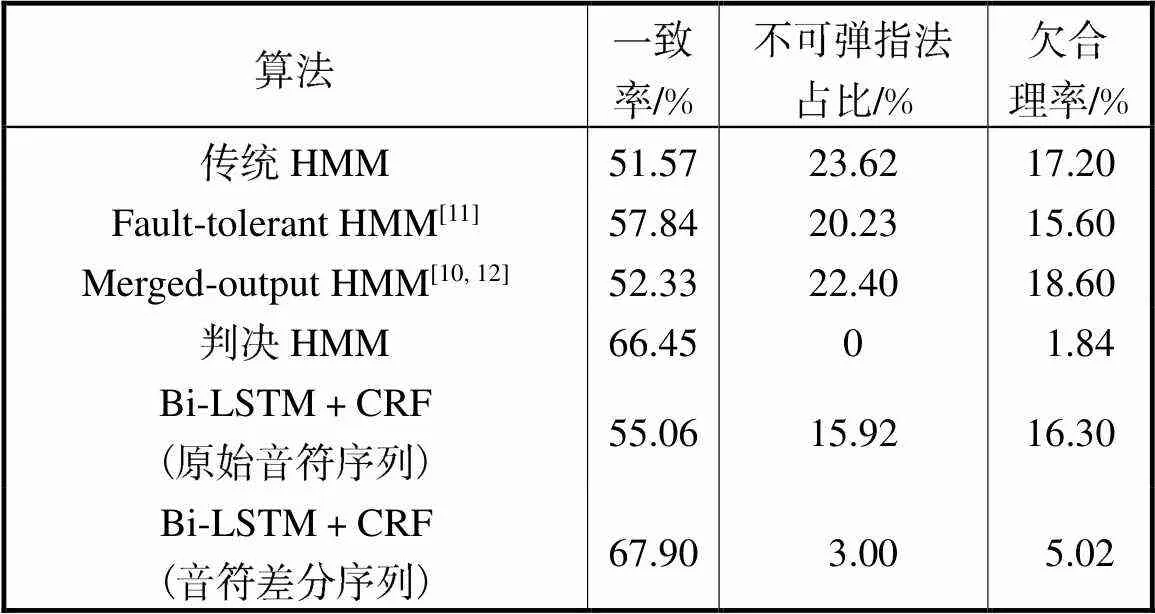
Tab.3 Comparison of labeling results of different algo-rithms

另外，为了对比传统方法与基于深度学习的方法，还与Bi-LSTM＋CRF模型进行了比较，图9为Bi-LSTM网络结构图，用LSTM的输出作为CRF的指法状态特征分数，并初始化指法转移特征分数矩阵，目标函数是极小化负对数目标序列分数，提高与人工标注的一致率．实验中分别输入音符序列和音符差分序列进行训练，输入的音符或音符差分数据均设为32维的随机word-embedding，采用Adam优化方法，学习率设为0.01．

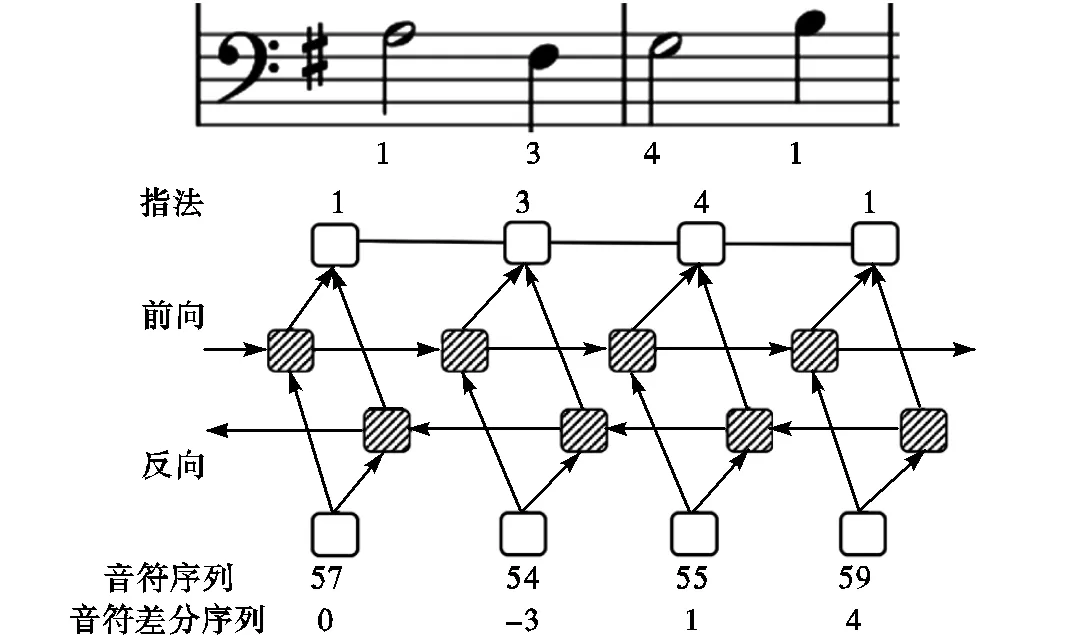
图9 输入为原始音符序列和音符差分序列的Bi-LSTM+CRF

训练好的模型采用Viterbi算法进行指法预测，经过对比，使用音符序列训练效果较差，一致率仅有55.06%，使用音符差分序列训练的一致率可以达到67.90%，较高于判决HMM，由此可见，较之指法和音符的一一映射关系，指法标注和音符差分信息关系更密切，本文提出的判决HMM恰恰也结合音符差分信息进行指法标注．但Bi-LSTM＋CRF仍存在3.00%的不可弹指法，欠合理率5.02%．因此从指法可弹性来看，本文算法优于Bi-LSTM＋CRF．

2.4.3 结果分析

本文提出的方法与人工标注的一致率仍有较大差距，分析原因有：一是由于指法的多态性且多态情况下没有明确的甄选标准，人工标注和算法均存在随机性；二是人工标注的最优指法权衡了演奏舒适度和演奏效率，虽然本文的算法考虑了这两方面因素，但目前尚缺少权威性的量化指标评价指法优劣；三是数据量不足，和弦标签数据匮乏．

在传统方法下，现有一阶隐马尔可夫模型用概率作为优化目标，模型参数描述能力有限，未能结合音符的长距离序列信息，也无法恰当地体现演奏舒适度和演奏效率．基于深度学习的方法利用神经网络强大的非线性拟合能力可以较为有效地提升一致率，但其优化目标只专注于提高一致率，指法可弹性仍需要提高．而本文算法在一致率和指法可弹性上做出了平衡．

3 结 论

(1)本文中提出了一种基于判决隐马尔可夫模型和改进维特比算法的钢琴指法自动标注算法．笔者结合指法规则的先验知识，首先在判决HMM中引入两种判决函数，有效克服了传统HMM不能结合音符序列信息的缺点，去除了错误的穿跨指和超出可弹跨度的指法．然后在预测指法路径时，根据先验知识对音符序列进行八度分段，并修改初始指法的确定方法，然后选择穿跨指数最少、演奏效率最高的指法序列为最优指法．通过一定量数据集的实验验证，相较之前的算法性能有了较大的提升．

(2)但目前受数据集规模的限制，算法还无法覆盖所有和弦的标注，目前在遇到数据集中未出现的和弦时，可以将和弦拆分成单音序列，按照单音标注指法组合起来作为和弦指法；并且模型只能标注基本指法，一些特殊指法如轮指(同音换指)、黑键指法规则等还需要进一步结合先验知识或加大相应的训练数据量．

(3)另外，为了对比传统模型和深度学习的方法，本文在同样的数据集上，采用Bi-LSTM+CRF构建了指法标注模型，初步实验结果其在一致率上较优于本文算法，但仍存在不可弹指法和较多转指，需要加大训练集并修改目标函数以提高指法标注性能．

［1］ Parncutt R，Sloboda J A，Clarke E F，et al. An ergonomic model of keyboard fingering for melodic fragments[J]. Music Perception：An Interdisciplinary Journal，1997，14(4)：341-382.

［2］ Jacobs J P. Refinements to the ergonomic model for keyboard fingering of parncutt，sloboda，clarke，raekallio，and desain[J]. Music Perception：An Interdisciplinary Journal，2001，18(4)：505-511.

［3］ Hart M，Bosch R，Tsai E. Finding optimal piano fingerings[J]. The UMAP Journal，2000，21(2)：167-177.

［4］ Kasimi A A，Nichols E，Raphael C. Automatic fingering system(AFS)[C]// 6th International Society for Information Retrieval Conference. London，UK，2005：1-4.

［5］ Kasimi A A，Nichols E，Raphael C. A simple algorithm for automatic generation of polyphonic piano fingerings[C]// 8th International Conference on Music Information Retrieval. Vienna，Austria，2007：355-356.

［6］ Nellåker E，Lu X. Optimal Piano Fingering for Simple Melodies[EB/OL]. https://kth.diva.portal.org/smash/get/ diva2:768564/FULLTEXT01.PDF，2014-12-04.

［7］ Lin C C，Liu D S M. An intelligent virtual piano tutor[C]// Proceedings of the 2006 ACM international conference on Virtual reality continuum and its applications，New York，USA，2006：353-356.

［8］ Viana A B，Cavalcanti J H F，Alsina P J. Intelligent system for piano fingering learning aid[C]// Proceedings of the 5th International Conference on Control，Automa-tion，Robotics & Vision. Singapore，1998：35-41.

［9］ Yonebayashi Y，Kameoka H，Sagayama S. Automatic decision of piano fingering based on a hidden markov models[C]// International Joint Conference on Artificial Intelligence. Hyderabad，India，2007：2915-2921.

［10］ Nakamura E，Ono N，Sagayama S. Merged-output HMM for piano fingering of both hands[C]// 15th International Society for Information Retrieval Confer-ence. Taipei，China，2014：531-536.

［11］ Sun Haotian，Guan Xin，Xian Jing，et al. Automatic marking of single-tone and chord piano fingering based on hidden Markov model[J]. Journal of Fudan University：Natural Science，2018，57(3)：84-91.

［12］ Hori G，Kameoka H，Sagayama S. Input-output HMM applied to automatic arrangement for guitars[J]. Information and Media Technologies，2013，8(2)：477-484.

［13］ Hori G，Sagayama S. Minimax Viterbi algorithm for HMM-based guitar fingering decision[C]// 17th International Society for Information Retrieval Conference. New York，USA，2016：448-453.

［14］ Hori G，Sagayama S. LP-Viterbi algorithm for automatic fingering decision[C]// Proceedings of the 14th Sound and Music Computing Conference. Banff，Canada，2017：386-390.

［15］ Huang Z，Xu W，Yu K. Bidirectional LSTM-CRF Models for Sequence Tagging[EB/OL]. http: //arxiv.org/ pdf/1508.01991v1.pdf，2015-08-09.

Automatic Fingering Annotation for Piano Score via Judgement-HMM and Improved Viterbi

Li Qiang，Li Chenxi，Guan Xin

(School of Microelectronics，Tianjin University，Tianjin 300072，China)

The existing first-order hidden Markov model(HMM)is used for piano fingering annotation without com-bining long-distance information of the note sequence．Therefore，an automatic piano fingering annotation algorithm based on decision HMM and the improved Viterbi algorithm is proposed．Taking prior knowledge of fingering into consideration，a judgment function was added to the traditional first-order HMM to remove wrong cross fingering and fingering beyond the bulletable span．During the prediction period，the optimization rules of the Viterbi algo-rithm were refined．First，the note sequence was segmented according to octaves，and the initial fingering method was modified．Subsequently，we chose a fingering sequence with the least number of cross fingering and whose performance was as efficient as that during optical fingering．To measure the performance of the proposed algorithm，two new evaluation metrics，the incapable-performing fingering ratio and the unreasonable fingering rate，were introduced to measure the flexibility and efficiency of fingering．Compared with the existing labeling model，the experiments showed that the proposed algorithm improved both the consistency rate and the two new in-dicators．In addition，to compare the performance of traditional methods with deep learning methods in small data sets，Bi-LSTM+CRF was added．The results showed that the inelastic fingering rate and unreasonable rate in deep learning were not as effective as those in the algorithm．

piano fingering；judgement-HMM；prior knowledge；improved Viterbi alogrithm

TP391

A

0493-2137(2020)08-0814-11

10.11784/tdxbz201907001

2019-07-01；

2019-08-20.

李 锵（1974—  ），男，博士，教授，liqiang@tju.edu.cn．Email：m_bigm@tju.edu.cn

关 欣，guanxin@tju.edu.cn.

国家自然科学基金资助项目(61471263)；天津市自然科学基金资助项目(16JCZDJC31100).

the National Natural Science Foundation of China(No.61471263)，the Natural Science Foundation of Tianjin，China (No.16JCZDJC31100).

(责任编辑：王晓燕)