基于车辆行驶轨迹的信号交叉口排队长度估计

姚 佼，戴亚轩，倪屹聆，韦 钰

(上海理工大学 管理学院,上海 200093)

0 引言

信号交叉口的排队长度是检测城市干道通行能力的关键参数之一，通常使用检测器来估计排队长度。在交叉口堵塞严重的情况下，排队车辆可能超过检测区域，形成长队列问题，此时难以用固定位置检测器来估计排队长度[1]。相关研究表明：交通信号的变化会对交叉口附近的干道交通流造成扰动，导致排队车辆时间和空间上的复杂变化。如今移动检测器可以实时更新车辆的最新位置，返回的交通信息数据用于重建车辆轨迹，进而建立排队长度估计模型[2]。

对于移动车辆的信息采集，张辉等人提出了一种基于信息标识识别来进行车辆定位的方法[3]；万芳等人基于信息采集设备数据和点检测器数据,构建了一种基于卡尔曼滤波的实时数据融合方法[4]；王庞伟等人基于城市车路协同系统动态获取路网信息优势，提出一种利用车路信息融合的实时交通状态评价方法[5]。进而，利用所采集到的移动数据对实时排队长度进行估计。Xu等人使用配备了智能基础设施合作系统的车辆，利用插值法对单交叉口进口道的车辆排队长度进行估计[6]；Liu等人基于网联车辆的实时数据，建立队列长度时间序列，利用马尔科夫链模型进行排队长度估计[7]；王东柱等人提出了一种基于网联车的停车点数据计算交叉口前车辆排队长度的方法[8]；庄立坚等人提出了一种基于低普及率的网联车数据，利用队尾网联车位置估算最大排队长度的方法[9]。将虚拟线圈检测器(Virtual Loop Detector, VTL)与移动检测器技术结合更是使此类研究逐渐成为热点。Hoh等人提出了VTL的概念，用于获取通过车辆的位置、时刻和速度信息[10]；Ban等人利用VTL系统，使用从移动检测器收集的交叉口行程时间来估计信号交叉口的实时队列长度[11]；Hao等人基于VTL系统，提出了一种基于运动方程的方法来研究车辆的排队位置，进而估计一个周期的排队长度；他们还基于贝叶斯网络方法，结合VTL系统使用移动检测器收集的网联车行程时间来估计信号交叉口的排队长度分布[12]。

但这些方法都是假设排队不会超过上游VTL的情况下提出的，如果车辆在进入VTL区域之前排队并且形成了长队列，则测量延误与车辆的实际延误不一致，不能用这些方法进行估计排队长度。针对这一问题，Izadpanah等人提出了一种基于轨迹的冲击波检测模型，识别网联车形成波与行驶轨迹的交点，使用线性回归模型来估计排队长度[13]；Cheng等人提出了一种从车辆轨迹中提取关键点来判断其运动状态，进而基于冲击波模型来估计交叉口实时排队长度的方法[14]；Hao等人提出了一种利用重建车辆运动轨迹来计算延误，进而建立排队长度估计模型的方法，但其排队长度等于队尾网联车到停车线的距离，忽略了后续加入的排队车辆[15]。

综上所述，现状大多数对于排队长度估计的研究在遇到长队列问题时会比较棘手，且忽略了后续排队车辆。本研究旨在使用移动检测器在VTL区域中收集轨迹信息进行排队长度估计，特别是利用VTL区域内所能获取的较短的车辆轨迹来解决长队列问题，使用车辆轨迹重建方法估计样本车辆的总交叉口延误。当车辆减速通过上游VTL时，应用简化车辆跟随模型；当车辆加速通过上游VTL时，基于LWR理论使用排队消散模型重建其排队轨迹，在重建缺失加速行驶轨迹之后，基于延误最小化方法估计队尾车辆到停车线的距离。最后根据各个车辆与队尾可收集行驶轨迹网联车的距离不同，对其到达率赋予不同的权重计算总的排队长度。

1 交叉口车辆的排队特点分析

图1描绘了一个信号交叉口中一部分车辆的行驶轨迹信息，X轴表示经过的时间，Y轴表示到停车线的距离(正值表示停车线的上游位置)，长队列VTL1为当排队长度超过97.5 m时所设置的虚拟线圈检测器,短队列VTL1为当排队长度大于37.5 m且小于97.5 m时所设置的虚拟线圈检测器,VTL2为设置在停车线另一侧97.5 m的虚拟线圈检测器，VTL1与VTL2共同组成了VTL区域。如果上游VTL1足够远，如图水平粗实线所示，距离停车线97.5 m，则到达流量可视为自由流量；如果上游VTL1靠近停车线，如图水平粗虚线所示，距离停车线37.5 m，则认为通过上游VTL1的车辆受到未检测到的交通流干扰。

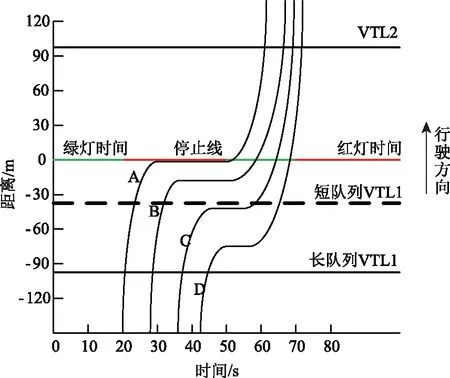
图1 不同位置车辆的行驶轨迹图Fig.1 Curves of traveling trajectory of vehicles at different locations

每个排队车辆的交叉口延误由3部分组成：减速延误，排队延误和加速延误，而自由流车辆没有任何延误。对于每辆车，我们首先根据VTL区域捕获的短轨迹确定车辆是否排队以及其所属延误方式，再根据排队中的不同车辆类型进行排队长度的估计。其中有4种可能的车辆类型：(1)A位置车辆：以自由流速通过上游VTL1，然后减速停止并加速到VTL区域内；(2)B位置车辆：减速进入VTL1区域，然后因排队停止再加速通过交叉口；(3)C位置车辆：加速进入VTL区域并直接离开交叉口；(4)D位置车辆：以自由流速通过VTL区域的车辆。

2 交叉口停车线前3种典型位置车辆的排队估计模型

2.1 A位置车辆的排队长度估计模型

通过VTL测量的A位置车辆的延误与交叉口延误完全相同，交叉口延误在一个周期内近似于线性减少。我们使用最后一个A位置排队车辆的轨迹作为输入，基于延误模型，利用延误减小到零的时间来估计一个信号周期内的排队长度。在本研究中，我们使用车辆数来表示排队长度。

研究表明，当车辆行驶速度不同时，队列的车头间距也会不同[16]。假设队列中第1辆车的排队位置为0，以车辆数量表示最后一个A位置排队车辆在队列中的位置：

LA=kjDA+1,

(1)

式中,kj为交叉口的特定堵塞密度；DA为最后一个A位置排队车辆到停车线的距离。

最后一个A位置排队车辆在无交叉口延误的情况下到达停车线的时间(NAT)：

(2)

车速对于排队队列既有相互制约的关系，也有相互独立的关系。车速影响着队列行驶状态，导致车头时距发生变化[17]。一个周期内的排队长度：

(3)

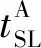
2.2 B位置车辆的排队长度估计模型

2.2.1 基于简化车辆跟驰模型的减速过程重建

我们假设第1辆车在不同周期到达交叉口时有相同的减速行为[18]，跟随车辆与主车辆具有基本相同的时空轨迹，因此身后的排队车辆遵循相同的轨迹进行减速。

设S=Y(t)是某个给定排队车辆的时空轨迹函数，则：

S+ΔS(x)=Y[t+Δt(x)]，

(4)

式中，S为从车辆到停车线的距离；ΔS(x)为车辆在位置上的变化量；x为主车辆的累积流量；t为实际时间；Δt(x)为车辆在时间上的变化量。

车辆在点(a，b)处的速度如下，并令G(*)为-Y(*)的反函数：

(5)

t+Δt(x)=G(c)。

(6)

因此，减速中任何轨迹点的坐标都可以表示为累积流量x和速度c的函数：

a(c,x)=G(c)-Δt(x)，

(7)

b(c,x)=Y[G(c)]-ΔS(x)。

(8)

第x*辆的坐标为：

a(c,x*)=G(c)-Δt(x*)，

(9)

b(c,x*)=Y[G(c)]-S(x*)。

(10)

取式(9)的一阶导数：

(11)

当已知车辆通过VTL1的时间和速度时：

a(c1,x*)=t1，

(12)

b(c1,x*)=d1，

(13)

式中，c1为车辆在VTL1处测量的速度；t1为车辆在VTL1处测量的时间；d1为从VTL1到停车线的距离。

减速过程中任何速度c下的相应轨迹点的坐标：

(14)

(15)

2.2.2排队长度估计

由图2所示，我们可以得到车辆开始从自由流速度开始减速时的坐标，并通过绘制假想自由流车辆轨迹来估计B位置车辆的NAT。

将自由流速度cf代入式(11)，我们可以得到车辆开始从自由流速度减速时的位置坐标(af，bf)。通过图2可以得到B位置车辆的NAT：

(16)

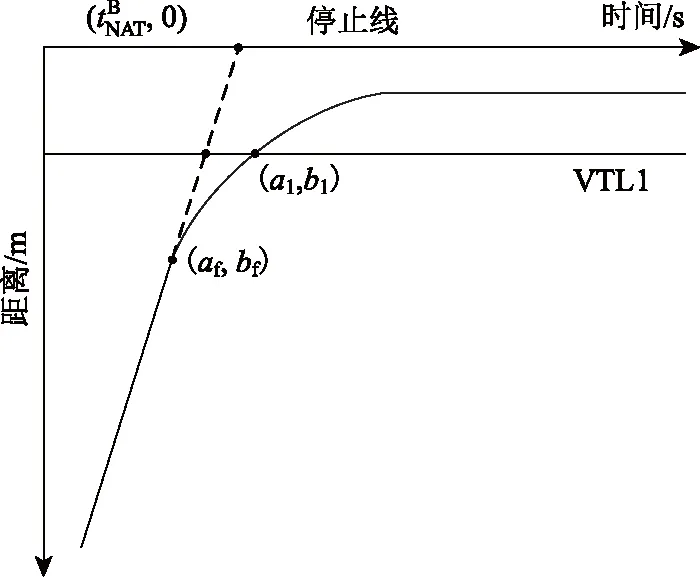
图2 B位置车辆的NAT计算Fig.2 Calculation of NAT for vehicle at position B

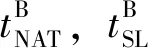
(17)

2.3 C位置车辆的排队长度估计模型

2.3.1 排队消散模型

基于Lighthill、Whitham和Richards(LWR)理论，密度k和流速q之间有如下关系：

(18)

对于均匀的路段，流速q是某些给定函数M密度k的函数：

q(a,b)=M[k(a,b)]。

(19)

因为M[k(a,b)]=M(k)，这个方程独立于a和b，则q(a,b)的偏微分方程为：

(20)

因此，q(a,b)沿由以下微分方程定义的直线特征曲线保持不变：

(21)

式中，N为在流速为q和密度为k时的波速，也可以认为是流密度基本图中点(a，b)处切线的斜率。

我们可以计算出沿着速度特征线c时x的变化率：

(22)

将(a0，b0)为由x(a，b)=0定义的曲线上给定速度的点。在时间为a，速度为c时特征线上的累积流量为：

x=(kN+q)(a-a0)。

(23)

然后沿着速度特征线计算，相应的(a，b)坐标如下：

(24)

(25)

2.3.2 基于交通流理论算法的加速过程重建

当时间为ai和位置为bi时，第i辆A/B位置车辆加速到速度c，此时：

(26)

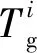
我们利用线性拟合的方法来找到合适的斜率和截距，以最大限度地减少时间误差：

(27)

我们需要找到零速特征线和车辆轨迹相交的车辆排队位置，排队消散模型如图3所示。根据位置与时间、速度的关系：

(28)

所以b的总导数为：

(29)

对式(29)进行计算可得：

(30)

(31)

该微分方程的解为：

(32)

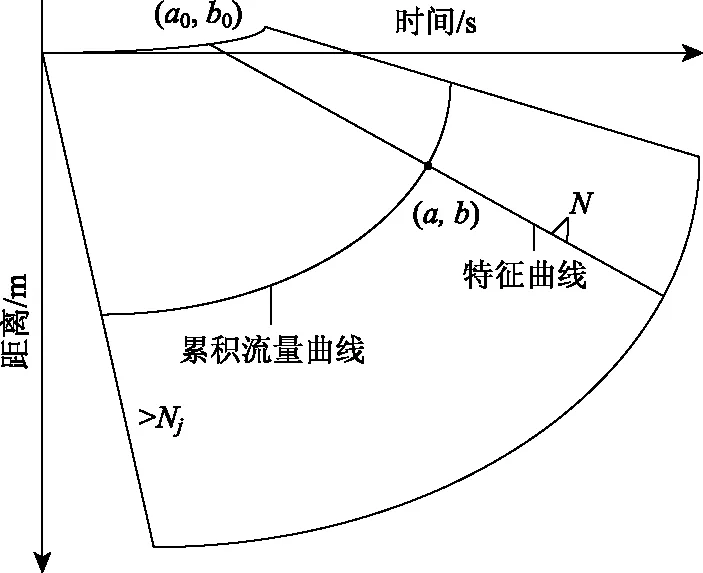
图3 排队消散模型Fig.3 Queue dissipative model

2.3.3 排队长度和排队位置估计

对于C位置车辆，我们可以通过式(27)计算速度为0时刻的位置即b(0)，然后从重建的加速轨迹中找到队列位置。但是，由于无法准确估计C型车辆的NAT，我们无法使用式(2)直接估计队列长度。但是，最后一个C位置排队车辆的队列位置确定了该循环的队列长度的下限。即：

QC=LC=kjDC+1，

(33)

式中，LC为以车辆数量表示最后一个C位置排队车辆在队列中的位置；DC为最后一个C位置排队车辆到停车线的距离。

2.4 改进后的排队长度估计模型

一般认为，一个信号周期的排队长度等于可获得行驶轨迹的队尾网联车到停车线的距离，加上剩余红灯时间里队尾网联车上游车辆的排队长度，如图4所示。

图4 到达率原理Fig.4 Principle of arrival rate

我们认为剩余红灯时间内的到达率是稳定的，使用平均值表示到达率。计算队尾网联车下游中的各个网联车与其之间的到达率qi：

(34)

式中，qi为队尾网联车下游中的每一辆网联车与其之间的到达率；DL为队尾网联车到停车线的距离；Di为第i辆网联车到停车线的距离；h为平均标准车头间距；TL为队尾网联车进入排队的时间；Ti为第i辆网联车进入排队的时间。

根据与队尾网联车的距离来确定不同到达率的权重分配，距离越近则权重越大。

(35)

式中，ωi为加权系数，总和为1。

则剩余红灯阶段到达车辆数为：

(36)

式中Tr为剩余红灯时间。

因此，3种不同位置车辆的排队长度可以表示为：

3 案例仿真与分析

本研究选取上海市黄浦区西藏南路干道上的两个相邻交叉口(西藏南路—淮海中路、西藏南路—金陵中路)。这两个交叉口属于上海市一个小型路网，此路网位于黄浦区较为繁华地段，且交叉口处于该路网中的中心位置，无论是高峰小时交通量还是排队长度等参数在大部分交叉口中都具有一定的代表性。通过地图软件图新地球(LSV)投影网联车车辆行驶轨迹并筛选目标车辆在经过相应交叉口的行驶轨迹，分A，B，C这3类车型在交叉口遇到排队时的场景，对本研究模型的计算结果与微观交通仿真软件VISSIM仿真输出的真值进行分析比对。

在进行仿真试验时，对流量、土地利用以及车型的影响进行了考虑。流量影响主要是考虑到晚高峰时段流量急剧增加，排队长度会明显发生变化，并且排队长度会出现明显的增加。土地利用影响主要是考虑到平交口沿线正在进行地铁建设，这对于排队长度也有一定的影响，但这正好也能反映出对于交通运行的影响大小。车型影响主要是将不同车辆换算成了标准PCU进行计算。

本研究采用根据实际车辆进行参数标定的Wiedemann74模型来描述车辆在道路中的跟驰情况，它可以作为网联车辆的基本模型，主要用于城市内部交通，有利于对排队长度的研究。并且是VISSIM中自带的驾驶模型，不需要调用外部API，可以通过对其参数进行标定，使得仿真结果与实际测量数据的差异最小化。具体的参数标定结果如表1所示。

表1 基于Wiedemann74模型的主要参数标定结果Tab.1 Wiedemann74 model based calibration result of main parameters

案例中VTL1设置在离交叉口停车线37.5 m处，停车线两侧VTL均设置在距离停车线97.5 m处。VISSIM中导入实际路网，并做相应的道路渠化设置，输入高峰时段的小时交通量以及信号配时数据，仿真时长为3 600 s，对3种车型分别进行5次VISSIM实例仿真，仿真结果取5次仿真的平均值。两个交叉口采集的高峰小时交通量如表2所示。VISSIM仿真排队长度的仿真值与模型计算结果对比如表3所示。

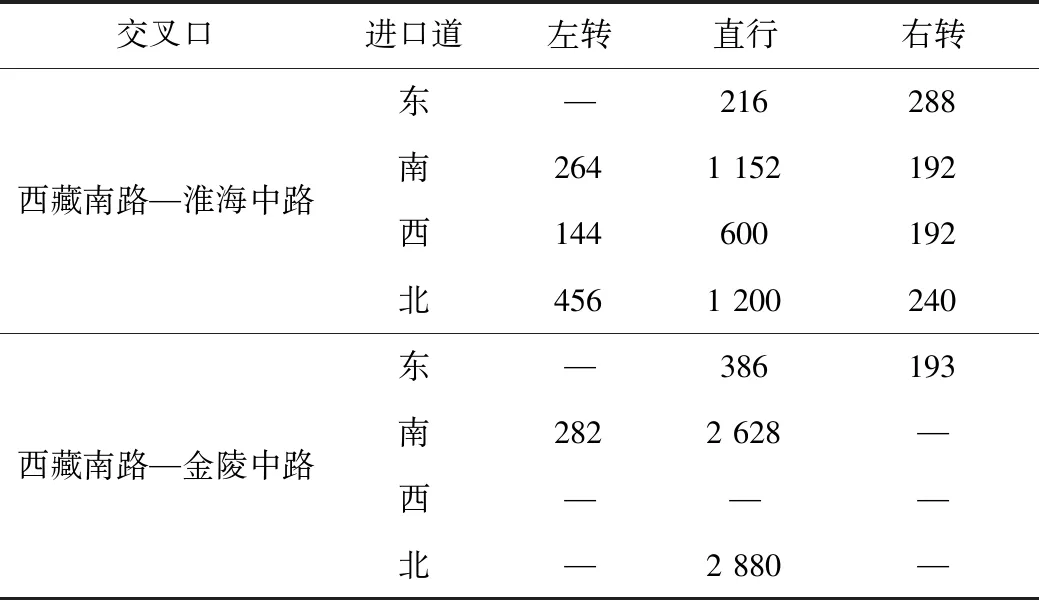
表2 案例交叉口高峰小时标准PCU统计(单位:pcu/h)Tab.2 Statistics of standard PCU at peak hours at case intersection(unit:pcu/h)

表3 排队长度的VISSIM仿真值与模型计算结果比对Tab.3 Comparison of queue lengths between value of VISSIM simulation and model calculation result

从表2中可以看出，两个交叉口各类车型模型的计算值和仿真真值最大误差为12 m，最小误差为1 m，如图5所示。此外，本研究模型的绝大部分计算结果较仿真真值偏小，可能是由于：(1)上述所研究交叉口位于上海市黄浦区中心地带，道路通行能力无法满足庞大的交通量，在高峰时段经常有交警进行交通疏导，与交通信号控制产生一定的冲突；(2)采集数据由于技术手段原因可能存在部分遗漏，造成误差，使得VISSIM仿真结果较大；(3)平均到达率小于实际到达率，排队长度估计偏大。

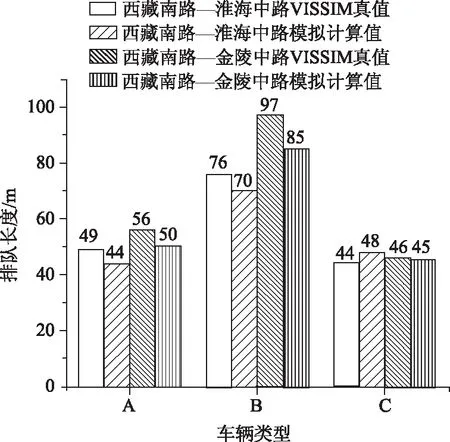
图5 仿真比对结果Fig.5 Comparison of simulation results

图6 相对误差对比图Fig.6 Comparison of relative errors

相对误差方面，两个交叉口各类车型最大相对误差为12.4%，最小为2.2%；平均为8.75%，方差为12.595%2，如图6所示。具体而言，西藏南路—淮海中路交叉口本研究模型与真值的最大相对误差为10.2%，最小为7.9%；平均为9.1%，方差为1.32%2；西藏南路—金陵中路的最大相对误差为12.4%，最小为2.2%；平均为8.4%，方差为29.9%2。此外，西藏南路—淮海中路的相对误差起伏不大，较为贴合平均值；而西藏南路—金陵中路的相对误差起伏较大，偏离平均值较大，但在可接受范围内，可能是由于：(1)西藏南路—金陵中路交叉口调查期间，周边存在地铁14号线的施工，部分交叉口进口道占用封道，造成通行能力下降；(2)部分进口道没有设置非机动车专用车道，在机动车与非机动车同时放行相位期间产生冲突，机动车通行能力下降；(3)VISSIM仿真软件中计算排队长度的模型对各项数据的精度要求高，数据采集时存在一定的误差，模型的参数标定亦有可能对结果产生影响；(4)两个交叉口之间的直线距离无法保证车辆在相邻交叉口顺畅行驶。

4 结论

基于车辆行驶轨迹研究排队长度，能够缓解交通控制对于固定检测器的严重依赖，并可以利用轨迹数据来估计交通控制所需的关键参数，为交通信号控制策略提供决策支持。本研究利用车辆行驶轨迹，分成A，B，C共3类车型，对交叉口队列中不同排队位置的车辆进行分析，建立了面向延误最小的排队长度估计模型；进而根据车辆与队尾网联车距离不同，对其到达率赋予不同的权重，计算总的排队长度。最后，对案例交叉口中投影在图新地球地图软件中的车辆行驶轨迹进行筛选，利用微观交通仿真软件VISSIM对本研究的模型进行仿真验证。仿真结果表明，本研究的排队长度估计模型与真值的平均误差为8.75%，方差为12.595%2，这说明本模型能够较为有效地估计城市道路交叉口的排队长度。但应该注意的是，本研究由于无法准确估计C型车辆的NAT，因此无法使用研究模型直接估计队列长度，需要在今后对其进行进一步的研究。另外，对于车辆在队列中的排队位置估计不够准确，容易造成模型计算结果的偏差，可以考虑通过对其进行约束条件的增加，确定车辆的排队范围，再进行排队位置的确定。