换热管流体激振的动力学特性及稳定性分析

冀 航

（兰州理工大学石油化工学院）

换热管是换热器中的重要部件，通常采取增加流速、 减薄换热管壁厚等手段提高换热效率。但在进行换热强化的同时，高流速意味着管路不稳定性的增加，可能会引起流体诱导振动［1］等多种形式的破坏，因此，为保证设备高效且安全运行，有必要对换热管流致振动的动力学特性和稳定性进行研究。

对于换热管流致振动，一部分是管程流体纵向流动产生的振动，另一部分则是由壳程流体横向冲刷引起的［2］。 由于折流板与换热管之间留有安装空隙，因此振动使换热管的相对位置发生变化，改变了流场形态，此时激振力会持续作用于换热管并使之振动，长此以往会对换热器造成严重的破坏，需要在设计时避免［3］。

针对换热管因流体诱导振动产生的不稳定性，Chen S S总结了两种基本的不稳定性机理，即速度机理和位移机理。 速度机理认为流体力与圆柱体流体的速度成正比，而位移机理认为流体力与圆柱体的位移成正比［3］。 当流体诱导振动的能量无法被自身完全消耗时， 系统产生不稳定性。然而在工程实际中，这两种不稳定性机理并不能很好地统一起来，并且对于振动的能量衰减与不稳定性之间的关系尚未存在明确的解释。

此外，国内外对于管程流体诱发振动的研究主要集中在对管路临界流速和对换热管自振频率的求解［4，5］，对换热管振动特性和流动稳定性并无明确的研究。

笔者将针对换热管的结构特点建立动力学模型并分析其振动特性，找出影响振动的因素和条件，并对其稳定性判据进行分析，可为换热器的设计与使用提供依据与指导。

1 换热管动力学模型的建立

与纵向流体的诱导振动相比，管外横向流产生的激振力更大，其振动也更为剧烈。 因此在工程实践中主要考虑流体的横向振动［6］。

可将换热管视为两端由管板固定，中间多个折流板简支的细长梁，取其中固支到简支的一段进行分析，考虑到换热管柔度较大，因此忽略轴向力和截面绕中性轴转动惯量的影响，其受力分析如图1所示。

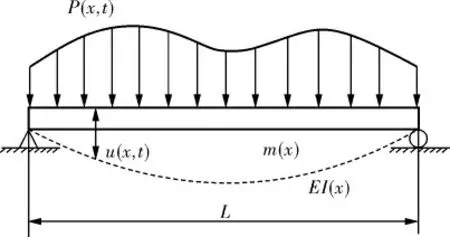
图1 换热管受力分析

取换热管上任意一微元体，其剪力与弯矩如图2所示。

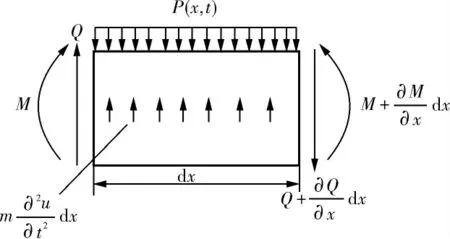
图2 微元体受力图

微元体的竖向平衡条件为：

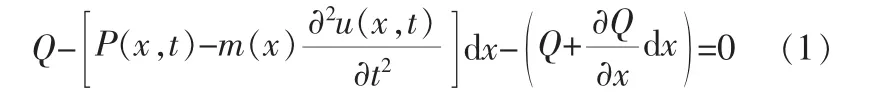
由此可得：

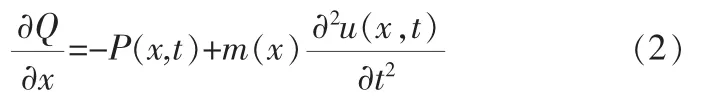
微元体右截面与x轴交点取矩：

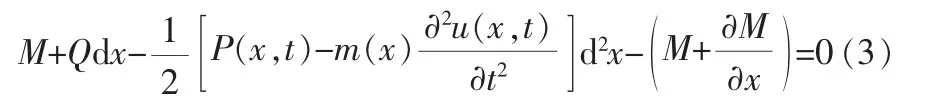
忽略二阶无穷小量，可得：

材料力学中梁的弯矩与变形的关系为：

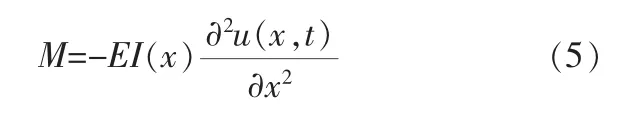
联立式（2）、（4）、（5），得到换热管的横向振动微分方程：

对于均质等截面的换热管，其横向振动微分方程可简化为：

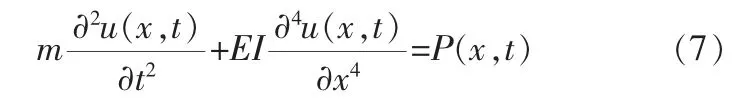
在换热管实际振动过程中，还必须考虑阻尼的影响， 换热管所受到的阻尼力来自于两部分，一部分是外界介质对换热管运动的阻抗，为外阻尼力； 另一部分则是由于振动导致的反复变形，沿换热管截面产生的分布阻尼应力， 为内阻尼力，二者阻尼形式均可视为粘性阻尼，其中外阻尼力是振速的函数，设其阻尼系数为c，即外阻尼力fn（x）可表示为：

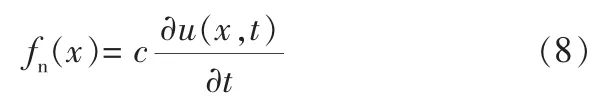
内阻尼力与材料应变速度成正比，设其阻尼系数为cs，则内阻尼力σi（x）可表示为：

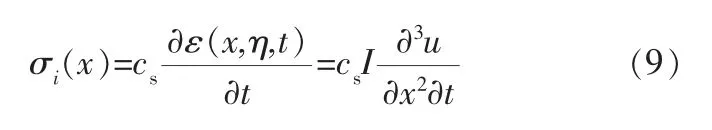
将式（8）、（9）代入式（7），则可得到换热管有阻尼振动的偏微分方程：

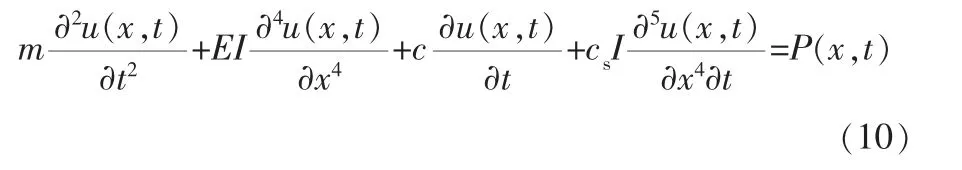
2 换热管动力学特性分析

对于式（10）而言，方程的左侧由惯性力、弹性力和阻尼力3个部分构成，右侧为激振力项，当P（x，t）=0时，即换热管不受外力作用时，其方程形式与弹簧-质量系统高度相似， 则可按照该模型进一步分析，换热管自由振动模型如图3所示。

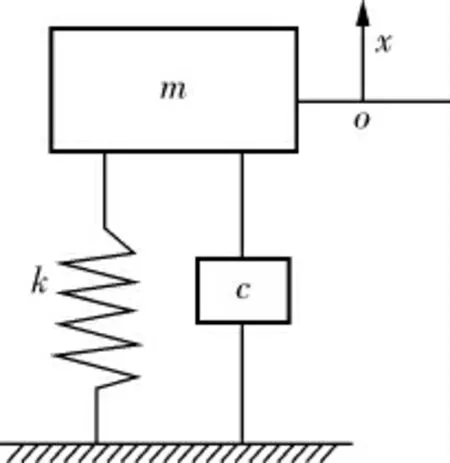
图3 换热管自由振动模型

对应的运动方程可以简写为：

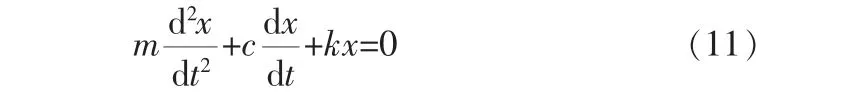
该方程的解形为：

考虑特征方程为复根的情况， 即λ1，2=-h±jω，其中：

故方程通解为：

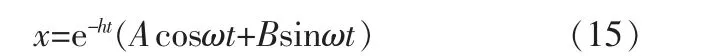
其中，A、B由初始条件决定，设t=0时，x=x0，则得到位移和速度的表达式为：

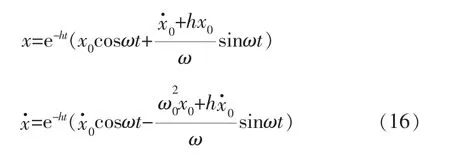
进一步改写为如下形式：

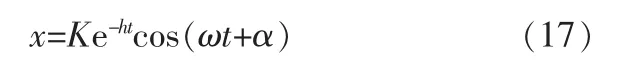
其中：

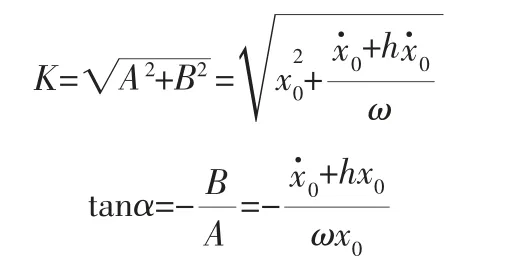
该形式的振动属于衰减振动过程，并且其振幅按照指数规律衰减。 系统相继两次通过平衡位置之间的时间间隔T=2π/ω。

对于图3所示的模型而言， 振动规律具有衰减振动特征，其表达式如式（17），此外，由于假设了阻力正比于速度，因此振动的最大值才会按指数规律衰减，故对数衰减仅适用于线性系统中。

3 换热管稳定性分析

得知微分方程（12）的解，便可求出所在的相轨线簇的方程， 在相平面x、y上的参数方程可写为：

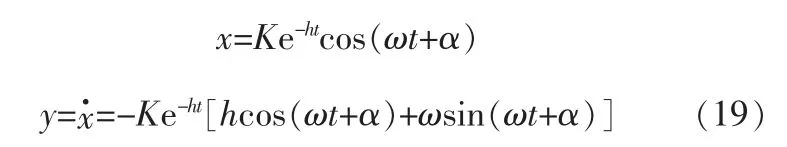
对x、y进行坐标变换，令u=ωx，v=y＋hx，记ωK=C1，则：

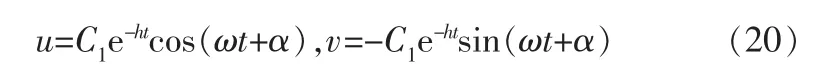
利用极坐标，可以使相轨线拥有更加简单的形式ρ=C1e-ht，φ=-（ωt＋α），消去时间，可得ρ=。这样， 可见相轨线在u、v平面上是一个以坐标原点为渐近点的对数螺线簇，具体如图4所示。

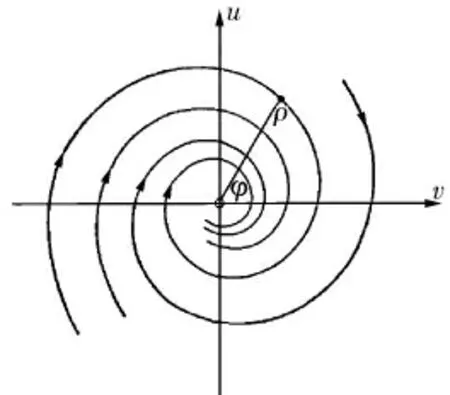
图4 u-v平面相轨线

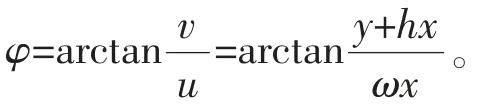
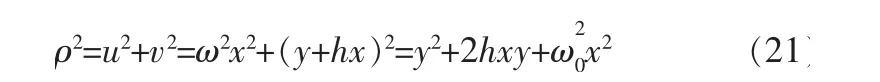
可得相轨线的坐标方程为：

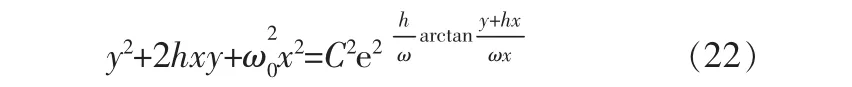
由于相轨线在做逆变换时不会改变定性性质，因此，x、y面上的相轨线簇也是以坐标原点为渐近点的螺线簇。

满足变换前的性质，因此，相邻的相径之间按指数规律衰减，其对数衰减率d=hT，做出表示全部可能运动的图像，如图5所示。

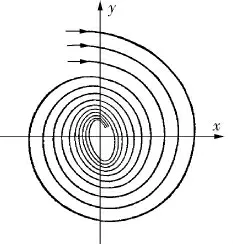
图5 x-y平面相轨线簇

由图4、5可见， 所有相轨线都对应于趋向于平衡位置的衰减振动，并且奇点满足李雅普诺夫稳定性条件，在相平面则表述为运动的稳定性与积分曲线的卷拢和展开有关，由于坐标的选择单值地决定了相点的运动方向，因此便可以单值确定奇点的稳定，反之，若螺线处于展开的形式，那么奇点就是不稳定的。 对应的稳定性条件则表示在方程（22）中，积分曲线卷拢的条件为h＞0，因为只有在这个情况下，沿顺时针方向运动时，其相径才会减小，系统最终才会趋于稳定。

进一步返回到方程（11）所表示的关系式中，则该稳定条件对应的物理意义为：系统的阻尼为正，且该过程中阻尼不断消耗系统能量，这种阻止运动且消耗功的正阻力不会引起不稳定，并且，若在无阻尼系统的平衡位置是稳定时，则存在阻尼时，该系统仍然是稳定的。

4 结束语

笔者采用理论分析方法研究了换热管受流体激振的动力学稳定性问题，首先建立了换热管流体诱导振动的动力学方程，并进一步对其振动特性进行分析，结果表明指数衰减振动仅存在于线性系统当中；其次，结合李雅普诺夫稳定性判据，推导出换热管受流体激振的稳定性对应于换热管动力学方程在相平面内积分曲线的卷拢状态，结果表明当相径减小时，系统最终趋于稳定。此外，分析了系统阻尼对稳定性的影响，结果表明正阻尼不会引起系统不稳定现象，对于初始平衡状态的无阻尼系统， 当存在正阻尼作用时，系统最终会保持稳定。