撞击式泡沫洗涤器流场数值模拟
李秋萍 韩 婕 刘德礼
(上海化工研究院有限公司)
撞击式泡沫洗涤器是一种采用独特的泡沫洗涤技术的新型湿式洗涤器,它具有高效、不易堵塞、操作弹性大及稳定可靠等特点,是气体净化领域的一项先进技术[1]。目前,该洗涤器已在废液(气)焚烧炉烟气净化、硫酸工业制酸尾气净化、复合肥工业尾气除尘净化、流化造粒(干燥)尾气净化、精对苯二甲酸(PTA)生产中的气流输送尾气净化、生活垃圾热解气净化及多晶硅工业的渣浆水解尾气净化等领域获得了工业应用,取得了良好的经济和社会效益[2]。
为了进一步对该技术进行优化,了解结构参数、 物性参数和操作参数对洗涤器性能的影响,需要对撞击式泡沫洗涤器展开系统的研究。 曾华星等借助CFD软件Fluent对动力波洗涤器的压力损失进行了数值模拟研究,但未分析洗涤器内部速度分布[3,4];李萌等采用RNG k-ε湍流模型和欧拉双流体多相流模型模拟了气液逆流接触洗涤器内的两相流场,并用湍流强度来表征泡沫区的大小[5];李光晓等采用溶氧法、电导探针法等考察了操作参数对气液逆流撞击的洗涤器内两相流型、传质性能和局部气含率的影响,定量分析了不同流型的传质效果[6];满长卓等通过冷模实验对气液逆流式洗涤器流动传质特性进行了考察,提出“两段式”流动-传质模型,该模型将洗涤器内气液作用区分为旋转射流段和高效传质段两个区段[7]。
笔者采用k-ω湍流模型和拉格朗日两相流模型对撞击式泡沫洗涤器进行数值模拟研究,希望了解洗涤器内部的流场分布和气液两相的相互作用机制,探索用液体浓度分布来定量表征泡沫区(有效传质区)的范围,同时考察不同工况下的洗涤器压降模拟结果, 并与试验结果相对比,验证模拟的可靠性,为撞击式泡沫洗涤器的研究和应用提供依据。
1 工作原理
撞击式泡沫洗涤器是基于撞击流(impinging streams)理 论[8,9]的 一 种 湿 式 洗 涤器,其工作原理如图1所示,待处理气体自上而下高速进入洗涤管,洗涤液由特殊结构的喷嘴自下而上喷入气流中,具有一定流速的气液两相在洗涤管中逆向对撞,当气液两相的动量达到平衡时,形成一个高度湍动的气泡和液滴共存的泡沫区[10]。 在泡沫区,气液两相呈高速湍流接触,接触表面积增大,同时接触表面由于气泡的不断生成和破裂而迅速更新,达到高效传热、传质的效果。
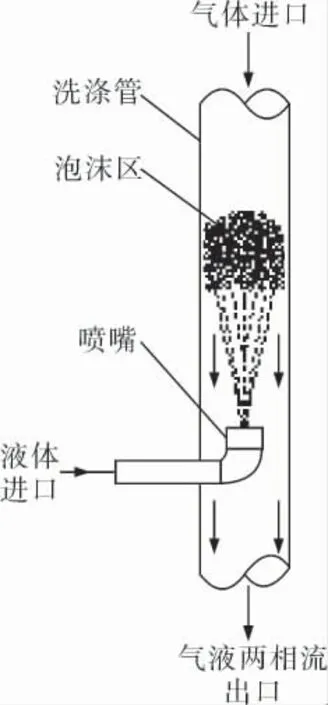
图1 撞击式泡沫洗涤器工作原理示意图
2 数值模拟方法
2.1 计算模型
由于该撞击式泡沫洗涤器的操作气速大于3m/s,气相雷诺数远大于4 000,属于湍流流动,故气相采用湍流模型,而液相在整个系统中的浓度较低, 所以采用离散相模型 (Discrete Phase Model,DPM)。
2.1.1 湍流模型
标准k-ω湍流模型是基于湍动能和耗散(k-ε模型)的经验模型,ω为耗散率,可以看成耗散ε对湍动能k的比值。 k-ω模型对流动中低雷诺数效应、 可压缩性和剪切流扩散做了针对性改进,能对剪切流(涡产生机理)进行更为准确的模拟。 为此, 采用标准k-ω湍流模型模拟洗涤管中气体的湍流流动。
标准k-ω模型的方程为[11]:

式中 Gk——基于平均速度梯度的湍动能产生项;
Gω——ω的产生项;
k——湍动能;
Sk、Sω——由用户的特殊要求产生的耗散项;
t——时间;
ui——气相i方向速度;
Yk、Yω——因湍流造成的k、ω的耗散;
ρ——流体密度;
ω——耗散率;
Γk、Γω——k、ω的扩散率。
2.1.2 离散相模型
采用欧拉-拉格朗日两相流模型 (简称拉格朗日两相流模型或离散相模型)对离散相进行模拟,此模型可以模拟多相分离流及相间的相互作用,还可以对各相进行单独计算,每相都有单独的守恒方程,具有很大的适应性。
在离散相模型中, 基础相当成连续介质,求解N-S控制方程,而大量的颗粒、气泡或液滴当成离散相使用拉格朗日方程进行轨迹跟踪求解,连续相和离散相之间可以通过各种模型进行动量传递、质量传递和能量传递。
在本模拟分析中,用球形颗粒(代表液滴或气泡)构成的第2相分布在连续相中,并与连续相发生碰撞等相互作用。 颗粒的作用力平衡方程为:

式中 CD——曳力系数;
dp——颗粒直径;
Fx——附加的加速度;
gx——重力加速度;
Re——相对雷诺数;
u——流体相速度;
up——颗粒速度;
ρ——流体密度;
ρp——颗粒密度(骨架密度);
μ——流体动力粘度。
2.2 模型网格划分
采用洗涤管直径为200mm的撞击式泡沫洗涤器,据此建立三维模型并在ICEMCFD中划分网格,然后将三维模型导入ANSYS Fluent 18.0的计算模块中。 考虑边界效应,根据速度梯度构建高密度边界层网格。
2.3 求解方法及控制方程离散格式
计算中,气体流动速度远低于可压缩气体流动的界限(0.3倍音速),亦不考虑温度变化,系统整体压降在千帕的数量级,所以气相可当作不可压缩流体处理。 笔者采用SIMPLE算法对压力-速度耦合方程、湍流方程进行变量分离求解,压力采用二阶格式离散,动量、湍动能及耗散等变量采用二阶迎风格式进行离散[11,12]。
2.4 边界条件
撞击式泡沫洗涤器内气液两相分别为空气和水,在工况1时的边界条件如下:
空气入口流量 1 215Nm3/h
空气入口压力 0Pa
水流量 7m3/h
喷射速度 11m/s
颗粒大小 0.5~1.5mm (平均1.2mm, 按照rosin-rammler规律分布)
3 试验部分
试验流程如图2所示,在引风机的作用下,待处理气体由气体进口进入洗涤管,洗涤液通过循环泵由喷头喷入气流中, 气液两相充分接触混合,洗涤后的气体与洗涤液一同下行,然后进行气液分离,洗涤液进入储液槽,净化气体经除沫器除去夹带的液沫后由引风机放空。
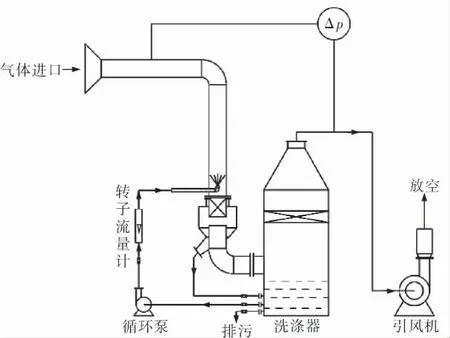
图2 试验流程示意图
喷嘴上方的垂直洗涤管材料为有机玻璃,内径200mm,高1 000mm;储液槽材料为不锈钢,内径700mm,高2 500mm。试验所用气体介质为常温空气,液体介质为常温水。 通过风机变频器调节操作风量, 风量的大小采用涡街流量计测量;洗涤水流量用转子流量计测量,洗涤器压降由差压变送器在洗涤器的进出口测得。
在5种工况下, 试验测得的撞击式泡沫洗涤器的压降值列于表1。

表1 不同工况下洗涤器压降的试验结果
4 结果与讨论
将喷嘴出口截面处设为0mm(Z0截面),向上为正方向,依次划分为50(Z1截面)、100(Z2截面)、150(Z3截面)、200(Z4截面)、300(Z5截面)、400(Z6截面)、500(Z7截面)、600(Z8截面)、700(Z9截面)、800(Z10截面)、900(Z11截面)、1 000mm(Z12截面)。
4.1 截面速度矢量
图3为气液两相相互作用时中心截面速度矢量图。 从图3可以看到, 根据混合流体的流动情况,可以把喷嘴上方分为3个明显不同的区域。
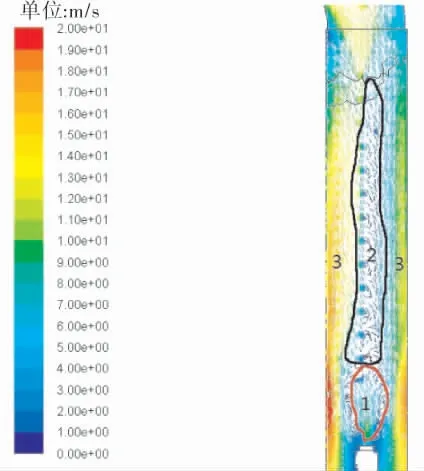
图3 中心截面速度矢量图
区域1中心部分液滴刚从喷嘴喷出, 具有最大的动能,中心气体被液滴带着向上流动,出现回流,这个区域定义为回流区域。 此时,液滴还没有到达洗涤管管壁附近, 因此气体没有受到阻挡,流动方向向下。 由于中心区域部分被液滴占据,气流通过的截面积变小,因此管壁四周附近的气体流速较高。 在中心区域气体速度向上,在管壁附近气体速度向下,因此在中心区域和管壁之间形成漩涡(图4)。
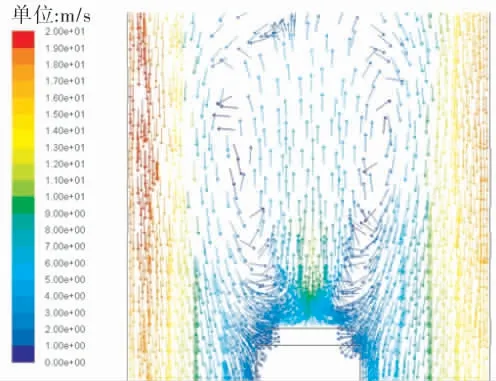
图4 区域1处的局部速度矢量图
区域2中,液滴继续向上运动,但已失去部分动能,液滴速度也越来越小,气相速度也较小,气液相相互纠缠,湍流增强,这个区域定义为泡沫区。
区域3中,形成了一条环形的气相主导区域,这个区域定义为壁面环流区域。 在该区域中,液滴被气相裹挟向下流动。
3个区域中, 区域1和区域2是最有效的传质区,因此扩大区域1和区域2,减小区域3的范围,可有效提高传质效果。 试验表明,通过提高喷射速度和液气比,可有效提高洗涤效率[13]。 这是因为:在其他条件不变的情况下,喷射速度提高,液相的动能提高, 可以携带更多的气体向上流动,回流区扩大;液气比提高,使得区域2扩大、区域3减小。
4.2 截面气相速度分布
图5为气液两相相互作用时3个截面上的气相速度分布。 由图5可以看出,3个截面径向速度分布不均匀,且处于喷头上方Z2=100mm处的速度变化梯度最大,洗涤管壁面附近速度最大,往管中心速度逐渐减小,在洗涤管半径R为40mm处速度最小,随后又逐渐增加,在洗涤管中心附近则高于Z5、Z9截面的中心速度, 这符合图4所示的规律,即气流在中心处出现回流。 随着高度的增加,壁面附近的速度有所减小,Z5、Z9截面处的气相速度在洗涤管中心处最小。 这是因为液相自喷嘴喷出后, 气相被挤压到沿管壁附近的环形通道中,所以管壁附近速度最大,同时由于液滴具有较大的向上冲击动能和携带作用,气相被液相携带在管中心附近出现回流,使此处的速度增加。 但是,随着高度增加,液滴动能逐渐减小,液滴对气相的影响也逐步减弱,回流消失,洗涤管中心处的速度减小。

图5 3个截面上气相速度分布
4.3 压降对比
影响撞击式泡沫洗涤器压降的主要因素是气体流速、液体喷射速度和液气比,按表1中的5种工况模拟计算了洗涤器的压降值,并与试验测得的结果进行对比(表2)。
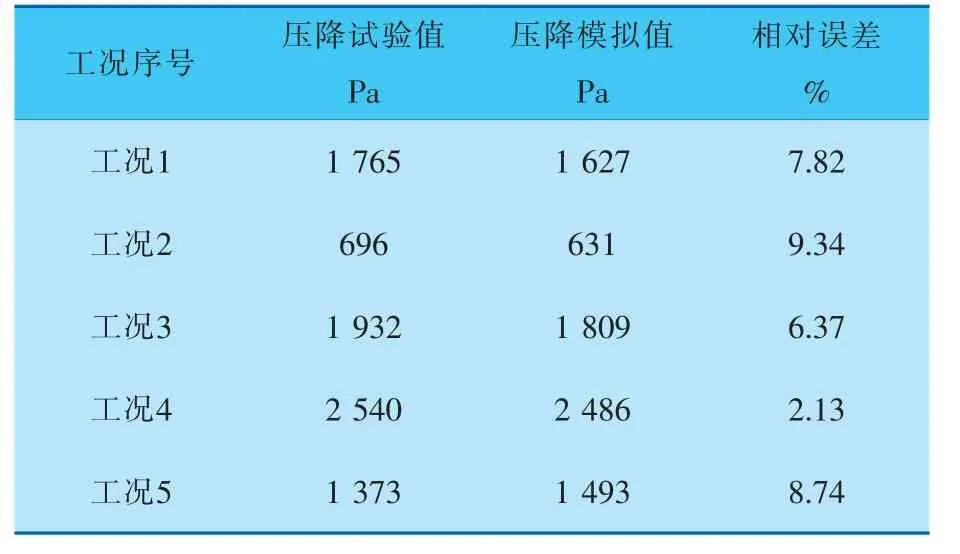
表2 洗涤器压降试验值与模拟值的对比
由表2可以看出, 撞击式泡沫洗涤器压降的模拟值总体小于试验值, 这是因为在模拟计算中,洗涤器管道壁面的压损未计算在内。 另外,可以看出压降的试验值与模拟值的相对误差均小于10%,吻合较好,表明本模拟运用的数学模型与计算方法具有一定的可靠性,可为撞击式泡沫洗涤器的研究与应用提供依据。
4.4 液相分布与浓度
图6所示的是Z3截面气相速度云图和液相粒子分布, 其中液滴颗粒用带有箭头的球表示,箭头表示液滴运动的方向,颜色代表速度大小。 从图6可以看到,随着距离喷嘴越来越远,液相颗粒以一定的角度向管壁处扩散, 最后充满整个截面,液相颗粒的速度逐步减小,液相对气相的影响也逐步减弱。 液相刚喷出时,气相被挤压到管壁附近的环形通道中,此处气相速度较高,而管中心处气相速度较低。
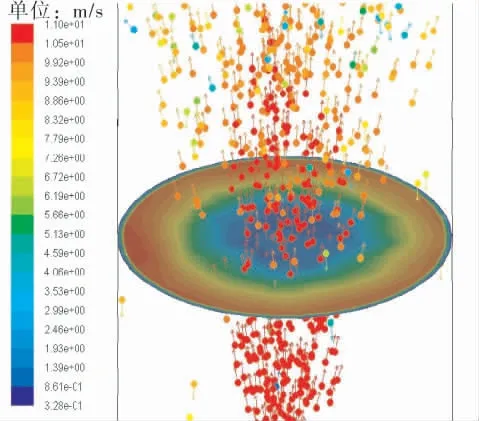
图6 Z3截面气相速度云图和液相粒子分布
为了定量表征泡沫区即有效传质区的范围,首先定义在没有气相干涉的情况下,液相的浓度为理论浓度C,其计算式为:

式中 A——洗涤管面积,m2;
QL——液相流量,m3/h;
vL——液相速度,m/s;
ρL——液相密度,kg/m3。
按工况1 (QL=7m3/h,vL=11m/s,ρL=1000kg/m3,洗涤管直径D=200mm)计算,液相的理论浓度C=5.6kg/m3。
图7为工况1时从模拟计算中截取的自喷嘴出口至1 200mm处各个截面上的液相浓度分布。由图7可以看出,从喷嘴出口往上,随着高度的增加,液相的浓度先增大后减小,浓度最大时约为21kg/m3。 在300~800mm高度范围内,液相浓度达到了理论浓度的3倍以上。 这是因为在这个区间内,气液相发生强烈的湍动,形成了所谓泡沫区(或称有效传质区域)。 在泡沫区内气液两相充分接触混合,接触表面积增大,达到了高效传质效果。 在相同的条件下,通过试验进行观察,同样在距喷嘴出口300~750mm高度范围内,可看到气液相发生强烈的湍动,形成了泡沫区(图8)。
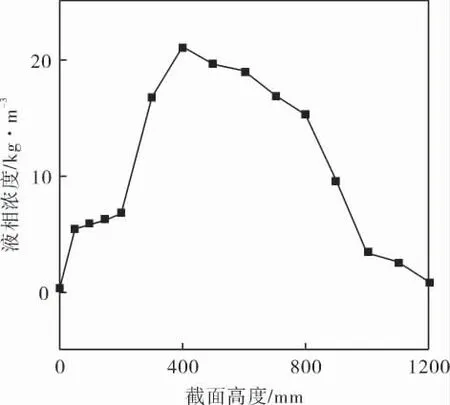
图7 不同截面的液相浓度

图8 泡沫区试验照片
5 结论
5.1 通过分析洗涤器内部的速度分布,将气液两相相互作用区分为3个不同的区域,即回流区、泡沫区和壁面环流区。
5.2 撞击式泡沫洗涤器数值模拟的压降值总体小于试验得出的压降值, 原因是在模拟计算时,洗涤管壁面的压损未计算在内。 5种工况下压降的试验值与模拟值的相对误差均小于10%, 吻合较好,验证了模拟的可靠性,可为撞击式泡沫洗涤器的研究与应用提供依据。
5.3 探索了用液相浓度分布来定量表征泡沫区的范围。 在洗涤管中,从喷嘴出口往上,随着高度的增加,液相浓度先增大后减小,在300~800mm高度范围内液相浓度达到了理论浓度的3倍以上,该区域即为泡沫区(有效传质区),这与试验观察到的情况相似。

