生存资料回归模型分析
——生存资料参数回归模型分析SAS实现
张甜甜 ,刘红伟 ,刘媛媛 ,李长平 ,2,胡良平
(1.天津医科大学公共卫生学院,天津 300070;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029;3.军事科学院研究生院,北京 100850
本期科研方法专题的第三篇文章介绍了生存资料参数回归模型有关的基础知识,包括构建三个常见的生存资料参数回归模型的基本原理、基于图示法判断生存时间服从何种概率分布的方法、基于最大似然估计法求解参数回归模型中的参数和两个参数回归模型拟合优度的比较。本文通过一个实例,利用SAS软件的LIFEREG过程介绍生存资料参数回归模型的SAS实现方法。
1 创建SAS数据集
【例1】本文所用数据是对149例糖尿病患者17年追踪调查数据,包括生存结局、生存时间、随访开始时年龄、体重指数等[1]。由于存在删失数据,此资料为生存资料。Diabetic数据集中生存时间(t,年)、随访开始时年龄(age1,岁)、体重指数(BMI)、诊断出糖尿病时的年龄(age0,岁)、收缩压(SBP,mmHg)和舒张压(DBP,mmHg)是定量自变量;吸烟状况(smk,0表示不吸烟,1表示曾吸烟,2表示吸烟)、心电图读数(ECG,1表示正常,2表示临界,3表示异常)、是否有冠心病(CHD,0表示无,1表示有)和结局(status,0表示截尾,1表示死亡)都是定性变量。利用以下SAS数据步程序,创建名为Diabetic的数据集:


【SAS程序说明】因篇幅所限,在CARDS语句后的数据仅列出前5个和后5个观测。因为收缩压和舒张压有一定关联[2],分析时取加权平均血压(MBP),即令 MBP=SBP*(1/3)+DBP*(2/3),权重系数分别为1/3和2/3。
2 图示法选择模型
2.1 SAS程序


2.2 主要输出结果
对数生存图、对数-对数生存图和对数失效比生存图分别见图1、图2和图3。

图1 对数生存图
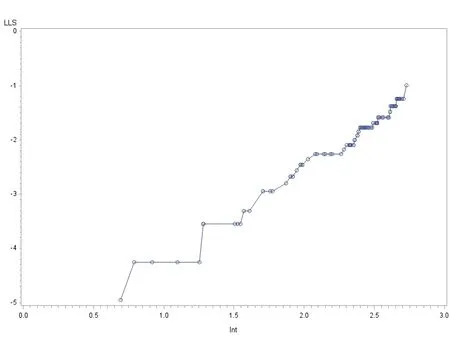
图2 对数-对数生存图

图3 对数失效比生存图
图1中的线图有些弯曲,图2在整体上呈线性趋势,与图3接近。图示法表明,基于现有数据,该生存资料同时适合Weibull分布模型和Log-logistic分布模型,本文选择Weibull分布模型进行拟合(图示法虽然简单直观,但不够精确,若深入探讨该数据是否更加适合Weibull分布模型,可参考其他方法[3])。
3 拟合参数回归模型
3.1 SAS程序
因为Weibull分布回归模型嵌套于广义Gamma分布回归模型[4],为选择最优的模型,本文将分别拟合Weibull分布回归模型和广义Gamma分布回归模型,根据似然比检验结果来确定最优模型。利用以下SAS过程步程序,构建Weibull分布回归模型和广义Gamma分布回归模型。


【SAS程序说明】采用LIFEREG过程分别拟合Weibull分布回归模型和广义Gamma分布回归模型,class语句列出离散型自变量,model语句左边为生存时间和生存结局变量(括号内为截尾值的标记),右边为预测变量(即自变量),包括离散和连续自变量。
3.2 主要输出结果
Weibull分布回归模型输出结果:

广义Gamma分布回归模型输出结果:
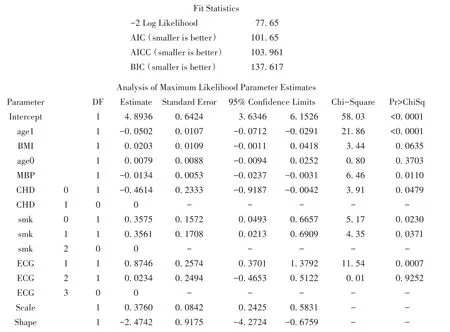
【SAS结果说明】Fit Statistics表是基于t为响应变量的最大似然估计得到的统计量,可以用来比较不同协变量的模型。Analysis of Maximum Likelihood Parameter Estimates表给出了参数的估计,包括预测变量的回归系数和参数分布中参数的估计值。其中“Scale”代表“尺度参数”,“Shape”代表“形状参数”。
4 参数回归模型拟合优度检验
因Weibull分布回归模型包含2个参数,广义Gamma分布回归模型包含3个参数,则似然比拟合优度检验[5]的自由度为 1,χ2统计量为 8.249(=85.899-77.650)(注意:;显然,8.249>6.635),P<0.01,即两个分布拟合效果之间差异有统计学意义,故采用-2logL值最小的分布,即广义Gamma分布(-2logL值为77.650)。广义Gamma分布回归模型输出结果中,只有age1、MBP、CHD、smk和ECG五个自变量有统计学意义。故仅保留这五个自变量,重新采用广义Gamma分布回归模型来进行分析。结果如下:
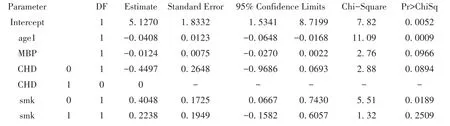

广义Gamma分布回归模型的分析结果表明,随访开始时年龄的回归系数为负值(-0.0408),说明随访年龄越大,生存时间越短,死亡风险越大;smk变量0水平与2水平比较时,对应的P值小于0.05,其回归系数为正值(0.4048),说明不吸烟者生存时间长于吸烟者;ECG变量1水平与3水平比较时,对应的P值小于0.001,其回归系数为正值(1.0879),说明心电图正常者生存时间长于心电图异常者。
5 讨论与小结
5.1 讨论
在现有的统计软件中,进行生存资料参数回归模型建模时尚不能筛选自变量,只能依据计算结果,采用手工方法删除没有统计学意义的自变量,这在一定程度上影响了最优回归模型的产生。当自变量中含有两个以上定量自变量时,根据统计分析的经验,尽可能产生出一些派生自变量(例如平方项、交叉乘积项等)参与构建回归模型,可能有助于找到拟合优度更好的回归模型。生存资料参数回归模型的建模策略与logistic回归模型建模策略类似,对最后的结果而言,保留在回归模型中的自变量,既要考虑其应具有统计学意义也要考虑其实际意义,即回归系数正负号的含义在专业上是可以得到合理解释的。
5.2 小结
本文通过一个实例,比较详细地介绍了基于SAS软件实现参数回归模型的拟合方法;通过图示法大致判断生存时间可能服从何种分布类型;最后,还针对所拟合的两个参数回归模型,进行了拟合优度检验,从而可以确定最优回归模型。需注意的是,当基于图示法确定生存时间符合某种参数分布且其对应的模型属于嵌套模型(特指其参数取某些特定值时,原先复杂的模型就退化成一个相对简单的模型,例如,当威布尔分布模型中的形状参数γ=1时,它就退化成指数分布模型了)时,则需要采用似然比检验确定拟合效果最优的模型;否则,需要根据所拟合的两个模型各自的参数数目和其他拟合统计量的数值,综合考虑后再选定相对较优的模型。

