生存资料回归模型分析
——生存资料及其统计分析方法概述
刘媛媛 ,李长平 ,2,胡良平
(1.天津医科大学公共卫生学院,天津 300070;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029;3.军事科学院研究生院,北京 100850
在医学随访研究中,有时观察结果并非在短期内能够出现,而需要长期随访观察,即采用追踪随访(follow up)的方式来研究事物发展和变化的规律,如了解某药物的长期疗效、手术后的存活时间、恶性肿瘤手术后复发时间等,这类资料属于随访资料[1]。由于随访资料的分析最初起源于对寿命长短的估计和预测,故称为生存分析或生存时间分析。评价某种疗法对疾病的效果时,研究者不仅需要观察是否出现了其感兴趣的终点事件(terminal event),还要考虑达到终点所经历的时间长短。因此,生存分析(survival analysis)是一种将是否出现终点事件与达到终点所经历的时间结合起来进行分析的统计分析方法[2],已广泛应用于医学研究领域,如现场追踪研究、临床疗效与安全性评价研究、疾病预后分析等,生存时间的涵义也随之拓展到更广的范围,又称为时间-效应分析(time-effect analysis)。与其他统计分析方法一样,生存分析方法和理论的使用范围较广,不仅应用于生物、医学、卫生、防疫和检验等领域,还可应用于工程科学、社会学、心理学、经济学、保险精算学等。因此,本文将对生存资料相关概念及其常用统计分析方法进行介绍。
1 概 述
1.1 生存分析的主要研究内容
生存分析主要研究的内容如下。①描述(估计):即根据生存数据估计其所来自的总体的生存函数、风险函数、概率密度函数以及由此而决定的其他相关指标(如中位生存期等),绘制生存曲线;②比较:即比较不同处理组生存数据的相应指标之间的差别是否具有统计学意义,最常见的效应指标是生存函数和风险函数;③影响因素分析:其目的是研究影响生存时间长短的因素,或在排除一些因素影响的情况下研究某个或某些因素对生存函数或风险函数等的影响;④预测:对具有不同因素水平个体的生存时间进行估计或预测[3]。
1.2 基本概念
1.2.1 生存时间和终点事件
生存时间(survival time)可以广泛地定义为从规定的观察起点到某一给定终点事件出现的时间。例如,一组精神疾病患者经过治疗出院后,记录他们在未来一个时期内各自出现复发的时间[4]。终点事件是研究者关注的事件,可以是某种疾病的发生、某种处理(治疗)的反应、病情复发或患者死亡等。
1.2.1.1 生存时间数据的分类
在临床研究中,研究时间一般是固定的,而患者是逐个进入试验,所以,根据观察结束时是否观察到终点事件,可将生存数据分为完全数据(complete data)和截尾数据(censored data)[5]。在随访研究的过程中,对某些观察对象已经观察到终点事件的发生,则称其为生存时间的完全数据,用t表示;在随访研究的过程中,若在观察期内由于某种原因对某些观察对象未能观察到终点事件(例如在临床疗效研究中,患者因车祸等意外死亡,不属于临床疗效的终点),不知道其确切的生存时间,则称其为生存时间的截尾数据或删失数据,用t+表示。产生截尾数据的原因大致如下:①失访;②至随访研究结束时结局仍未发生;③研究对象死于其他原因或出现严重药物反应而终止试验或观察。截尾生存时间的计算均为规定的起点至截尾点所经历的时间。
由于删失产生的原因不同,删失数据的类型也不同,主要有左删失、右删失和区间删失数据等类型。①左删失(left-censored):假设研究对象在某一时刻开始进入研究接受观察,在该时间点之前,研究者感兴趣的事件已经发生,但无法明确其具体时间,这种类型即为左删失数据;②右删失(rightcensored):在进行随访观察中,对研究对象观察的起始时间已知,但终点事件发生的时间未知,无法获取具体的生存时间,只知道生存时间大于观察到的时间,这种类型的生存时间称为右删失;③区间删失(interval-censored):在实际的研究中,如果不能够进行连续的观察随访,只能预先设定观察时间点,研究人员仅能知道每个研究对象在随访区间内是否发生终点事件,而不知道准确的发生时间,这种删失类型称为区间删失。
右删失数据又可以分为I、II和III型。I型右删失:从同一起点开始观察到某规定时间结束观察时,除了已经发生终点事件的研究对象外,其余研究对象的观察时间统一截止到某一固定时间点,这种删失类型即为I型删失。I型删失的删失时间是固定的,故又称为定时删失。I型删失不允许个体在研究的过程中退出。II型右删失:从同一起点开始观察到有一定数量的个体发生给定的事件,即在研究的过程中,一直随访观察到有足够数量的终点事件发生为止,此时研究停止,未发生终点事件的研究对象的生存时间未知,这种删失类型即为II型删失,又称为定数删失。II型删失可以理解为删失比例是事先已经设定的。III型右删失:在实际的研究过程中,往往研究期是固定的,并且研究对象在此研究期的不同时间进入研究,即观察起始时间不同。同时,在研究结束前,有些研究对象已经发生终点事件,可以记录其准确的生存时间,但也有些研究对象中途退出研究,或者在研究结束时仍未发生终点事件,他们的生存时间无法确定。这种观察起始时间和删失时间均不相同的类型,称为III型右删失,也是临床研究中最为常见的类型。由于删失数据往往是随机发生的,因此,III型右删失也称为随机删失。上述三种删失都是右删失,即其精确值未知,只知其大于或等于删失时间。
按观察次数分类,区间删失数据可分为I和II型。I型区间删失又称现况数据,指观察次数为1次,仅知道准确时间小于或大于观察时间,常发生在横断面研究和非致死性肿瘤致瘤性试验中[6]。II型区间删失,指观察次数为2次,所得观测数据中至少包括一个区间,观察时间点为相互独立的确定时间,主要发生在需要定期随访观察的研究中。
1.2.1.2 生存资料的特点
生存资料具有以下特点:①同时具有生存结局和生存时间;②生存时间可能含有删失数据或截尾数据;③生存时间的分布通常不服从正态分布,生存时间常呈指数分布、Weibull分布、对数正态分布等;④影响生存时间的因素较复杂且不易控制。
1.2.2 死亡概率
死亡概率(probability of death)用q表示,指某时段开始时存活的个体在该时段内死亡的可能性。如一年死亡概率表示年初尚存活的人口在今后一年内死亡的可能性,公式见式(1):

1.2.3 生存概率和生存率
生存概率(survival probability)用p表示,指某单位时段开始时存活的个体到该时段结束时仍存活的可能性。如一年生存概率表示该年年初尚存活的人口存活满一年的可能性,p=1-q,公式见式(2):

生存率(survival rate)又称生存函数(survival function),表示观察对象的生存时间T大于某时刻t的概率,以S(t)表示。生存率通常随时间逐渐下降,即0≤S(t)≤1。
若无截尾数据,生存率计算公式见式(3):

若有截尾数据,需要分段计算生存概率,假定观察对象在各个时段的生存事件独立,根据概率乘法运算法则计算生存率,公式见式(4)。为各时段的生存概率。

1.2.4 生存曲线与中位生存期
生存曲线(survival curve)是以观察(随访)时间为横轴,以生存率为纵轴,将各个时间点所对应的生存率连接在一起的曲线图。生存曲线是一条下降的曲线,生存曲线平缓,表示生存率高或生存时间较长;生存曲线陡峭,表示生存率低或生存时间较短。
中位生存期(median survival time)又称半数生存期,即恰好有50%的个体尚存活的时间。生存曲线纵轴生存率为50%时所对应的横轴生存时间即为中位生存期,反映生存时间的平均水平。中位生存期越长,表示疾病的预后越好;中位生存期越短,表示疾病的预后越差。
1.2.5 风险函数
风险函数(hazard function)又称危险率函数,表示生存时间已达t的观察对象在t到t+Δt时间区间内死亡概率的极限,即生存时间已达t的个体在t时刻的瞬时死亡率,公式见式(5):

1.2.6 概率密度函数
概率密度函数(probability density function)表示一个体死于(t,t+ Δt)小区间的概率极限,即t时刻的瞬时死亡率,公式见式(6):
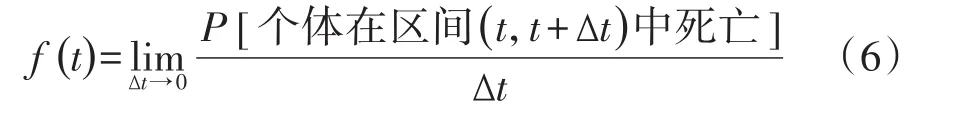
2 生存资料常用的统计分析方法
根据生存资料和统计模型的特点进行分类,常用的生存分析方法主要包括描述法、参数法、半参数法和非参数法;根据生存资料统计分析的主要内容进行分类,常用的生存分析方法主要包括生存资料的统计描述、生存曲线的比较和生存资料的回归分析。
2.1 按生存资料和统计模型的特点分类
2.1.1 描述法
根据样本观测值提供的信息,直接用公式计算出每一个时间点或时间区间上的生存函数、死亡函数、风险函数等,并采用列表或绘图的方式显示生存时间的分布规律。描述法的优点:方法简单且对数据分布无要求;缺点:不能对两组或多组生存时间资料所对应的分布函数进行假设检验,不能分析影响因素,不能建立生存时间与影响因素之间依赖关系的回归模型。
2.1.2 参数法
根据样本观测值来估计假定的分布模型中的参数,获得生存时间的概率分布模型、生存函数和/或危险率函数的估计值。生存时间经常服从的分布有指数分布、Weibull分布、对数正态分布、对数Logistic分布、Gamma分布等。参数法的优点:可以估计生存函数和/或危险率函数,可以对两个或多个生存分布函数进行假设检验,可以分析各因素对生存时间的影响,可以建立生存时间与影响因素之间依赖关系的回归模型;缺点:需要事先知道生存时间的分布类型。
2.1.3 半参数法
不需要对生存时间的分布做出假定,却可以通过一个回归模型来显示生存时间的变化规律以及各因素对生存时间的影响,常用的模型包括Cox比例风险回归模型等。相较而言,半参数方法比参数方法灵活,比非参数方法更易于解释分析结果。半参数法的优点:可以估计生存函数和/或风险函数,可以对两个或多个生存分布函数进行假设检验,可以分析影响因素对生存时间的影响,可以建立生存时间与影响因素之间依赖关系的回归模型,不需要事先知道生存时间的分布;缺点:不便于对高维、强相关数据进行有效的处理。
2.1.4 非参数法
随访资料生存曲线的估计方法有参数法和非参数法,对于服从特定概率分布的生存资料,参数法更准确;但大多数生存资料的分布不规则、不确定或未知,故常需选用非参数法。常用的方法包括Kaplan-Meier(卡普兰-迈耶)估计法和Life table(寿命表)估计法,另外,还有Lynden-Bell(林登-贝尔)估计法和Turnbull(特恩布尔)估计法[7]。非参数法的优点:可以估计生存函数,可以比较两个或多个生存分布函数,可以分析单个影响因素对生存时间的影响,对生存时间的分布没有要求;缺点:不能建立生存时间与影响因素之间依赖关系的回归模型。
2.2 按生存资料统计分析的主要内容分类
2.2.1 生存资料的统计描述
2.2.1.1 Kaplan-Meier估计法
Kaplan-Meier法又称乘积极限法,基本思想是将所有观察对象的生存时间(包括删失数据)由小到大依次排列,对每个时间点进行死亡概率、生存概率和生存率的估计[1],能够充分利用每条记录的信息,估计不同生存时间点的生存率。该法利用概率乘法定理计算生存率,一般用于小样本或大样本未分组资料。Kaplan-Meier法绘制的生存曲线为阶梯形曲线[2]。
2.2.1.2 寿命表估计法
当遇到样本含量较大的随访资料时,某些个体的删失发生在两次随访之间,不能获得确切的生存时间,这时需要将原始资料按生存时间分组后再进行分析,即寿命表法。它的应用早于Kaplan-Meier法,是Kaplan-Meier法的近似方法(频数表法)。该法不能够充分利用每条记录的信息,但其计算和结果的解释都很简单。一般用于观察对象数目较多的分组资料,根据随访时间和随访结果编制成频数分布表的形式。寿命表法绘制的生存曲线为折线形曲线[2]。
因篇幅所限,Lynden-Bell(林登-贝尔)估计法和Turnbull(特恩布尔)估计法从略,可参阅文献[7]。
2.2.2 生存曲线或生存时间的比较
当全部生存数据来自k个不同的处理组时,研究者往往需要比较k条生存曲线(或k个生存率)之间的差异是否有统计学意义,常用的假设检验方法包括对数秩检验(log-rank test)、威尔考克森检验(Wilcoxon test)、考克斯-曼特尔检验(Cox-Mantel test)和吉亨检验(Gehan test)[7]等。当生存时间的分布为Weibull分布或属于比例风险模型时,log-rank检验效率较高;当生存时间的分布为对数正态分布时,Wilcoxon检验效率较高,两种方法均是非参数检验方法。
2.2.2.1 对数秩检验(log-rank test)
Log-rank test也称为Cox-Mantel检验,该方法的基本思想是假定拟进行比较的不同总体生存函数之间差异无统计学意义,即H0成立时,根据ti时点的死亡率,可计算出各组的理论死亡数,并与实际观察到的死亡数进行比较。衡量观察数与理论数差别大小的统计量为χ2,服从自由度为(组数-1)的χ2分布,公式见式(7)。Log-rank检验给组间死亡的远期差别更大的权重,即对远期差异敏感。
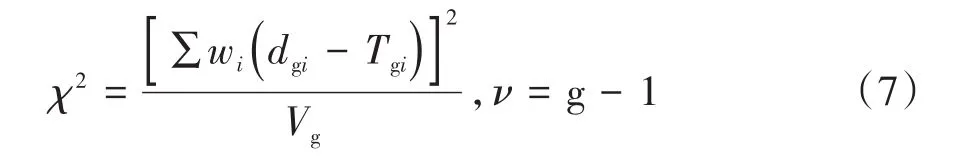

2.2.2.2 Breslow检验
Breslow检验又称广义Wilcoxon检验或Gehan比分检验,其基本思想同log-rank检验,两种方法在计算时的权重不同。公式同式(7),其中wi=ni。此检验给组间死亡的近期差别更大的权重,即对近期差异敏感。
Log-rank检验与Breslow检验两种方法的应用条件相同:即各组生存曲线呈比例风险关系,生存曲线不能有交叉。生存曲线有交叉时,不适合做生存曲线的整体比较。
2.2.3 生存资料的回归分析
以上两种生存曲线比较的统计分析方法均属于单因素分析方法,若研究者关心的影响生存时间的因素不只一个时,应采用适当的多因素分析方法,而普通的线性回归模型和logistic回归模型通常并不适用。如果仅考虑生存时间作为反应变量进行线性回归分析,由于生存时间通常并不是正态分布,不满足线性回归模型的要求;如果仅考虑某一时点事件结局作为反应变量进行logistic回归分析,则生存时间长短的信息又未能充分利用。此外,生存时间资料中还有删失数据,线性回归模型和logistic回归模型均不能利用这种不完全数据提供的信息。鉴于生存数据的上述特点,发展出了适用于生存数据统计分析的多种回归模型。
生存资料回归模型可以用来筛选影响反应变量的因素,并根据影响因素的不同取值对生存率(或危险率)进行预测。
按生存时间的分布类型,生存资料回归模型分析方法主要包括参数回归模型、半参数回归模型和非参数回归模型。若通过图解法或分布的拟合优度检验,得到待分析的生存资料服从某特定分布的参数回归模型时,如指数分布模型、Weibull分布模型等,则可应用相应的参数回归模型,这类参数回归模型常被称为“加速失效时间模型”或“对数线性回归模型”,此时可获得比盲目采用其他方法更准确的结果;若不服从某特定分布的参数模型,则可考虑应用半参数回归模型,常用的方法包括Cox比例风险回归模型。
按生存时间数据删失类型的分类,主要包括左删失、右删失和区间删失生存资料回归模型。
按是否满足比例风险(proportional hazards)假定,主要包括Cox比例风险回归模型、依时或非比例Cox回归模型,还有脆弱模型、参数加性危险率模型和非参数加性危险率模型等[8]。
按因变量的个数分类,可分为一元多重生存资料回归模型(绝大多数生存资料回归模型都属于这一类)和多元多重生存资料回归模型(如边际模型)。
3 讨论与小结
3.1 讨论
生存分析作为近三十年来发展起来的数理统计新分支,是根据医学、生命科学、可靠性工程、保险等科学研究中的大量实际问题所提出的。对于纵向研究或追踪随访数据,生存分析是一类常用的统计分析方法,但其应用对生存资料有一定的要求。比如,以Cox回归模型为代表的生存分析方法在数据缺失结构下能够利用偏似然估计理论辨识出对预后有影响的伴随变量,但当删失数据较多时,估计结果不够理想[9]。因此,如何基于现有的生存数据,得到更可靠的分析结果,已成为国内外统计学界研究的热点。现在,越来越多的研究者和数理统计学家尝试将生存分析与其他的理论相结合,形成了新的理论方法,并得到了较好的应用,如贝叶斯理论下的生存分析方法[10]。即便如此,仍然会存在诸多问题,所以,必然需要对统计学的理论和方法进行不断完善和创新。
3.2 小结
由于生存资料通常都带有删失数据,而且,删失机制不尽相同,故对生存资料的统计描述、差异性分析和回归分析都较经典统计分析方法复杂得多。正因如此,在选择生存资料统计分析方法时,应清楚待分析的生存资料的各种真实情况,在多种备选择的同类分析方法中,选择最合适的统计分析方法,以便准确地揭示生存资料的内在变化规律。

