生存资料回归模型分析——生存资料Cox比例风险回归模型分析

姚婷婷 ，刘媛媛 ，李长平 ，2*，胡良平

（1.天津医科大学公共卫生学院，天津 300070；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029；3.军事科学院研究生院，北京 100850

在对生存资料进行分析时，若同时分析众多因素对生存结局和生存时间的影响，需要采用多因素分析方法，而传统的多因素分析方法并不适用，不能同时处理生存结局和生存时间，也不能充分利用删失时间所提供的不完全信息。适用于生存数据的多因素生存分析方法主要有参数回归模型和半参数回归模型两类，参数法需要以特定的分布为基础建立回归模型，应用有其局限性，而半参数法的假定相对较少或较弱，特别是Cox比例风险回归模型（Cox's proportional hazards regression model），不要求生存资料满足特定的分布类型，是目前对生存资料进行多因素分析最常用的方法之一。

1 概 述

1.1 Cox比例风险回归模型简介

Cox比例风险回归模型见式（1）：

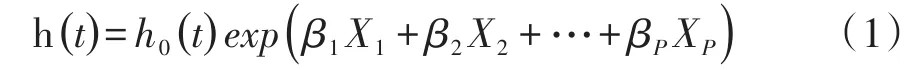
在式（1）中，X1、X2、…、Xp为与生存时间可能有关的自变量（即影响因素），其中的自变量或影响因素可能是定量的或定性的，在整个观察期内不随时间的变化而变化；h(t)为具有自变量X1、X2、…、Xp的个体在t时刻的风险函数；h0(t)为所有自变量为0时t时刻的风险函数，称为基准风险函数（baseline hazard function），是未知的；β1、β2、…、βp为各自变量的偏回归系数，是一组未知的参数，需要根据实际的数据来估计。

Cox模型不直接考察生存函数S(t)与自变量的关系，而是利用生存函数S(t)与风险函数h(t)的关系，将风险函数h(t)作为因变量，间接反映自变量与生存函数S(t)的关系。该模型右侧可分为两个部分：一部分为h0(t)，它没有明确的定义，分布无明确的假定，为非参数部分；另一部分是以p个自变量的线性组合为指数的指数函数，具有参数模型形式，其中回归系数反映自变量的效应，可通过样本实际观测值来估计。所以Cox比例风险回归模型实为半参数模型（semi-parametric model）［1-6］。

1.2 模型假定及其检验

由Cox比例风险回归模型可知，任意两个个体风险函数之比，即风险比（hazard ratio，HR）为：

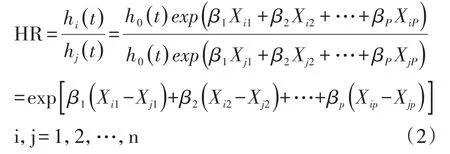
该比值与h0(t)无关，也与时间t无关，即模型中自变量的效应不随时间的改变而改变，具有某种特定预后因素向量的患者的死亡风险与具有另一种特定预后因素向量的患者的死亡风险在所有时间点上都保持一个恒定的比例，这种情形被称为比例风险（proportional hazard）假定，简称PH假定。

PH假定的检验方法包括图示法和检验法。图示法是通过观察散点图中散点的分布或趋势来判断生存时间是否满足或近似满足PH假定，主要有COX-KM生存曲线、基于累计风险函数的图示法、Schoenfeld残差图、Score残差图；检验法是通过构造满足PH假设下服从某一已知分布的统计量，基于检验统计量的数值大小和对应的P值来判断是否满足或近似满足PH假定，主要有时间协变量法、线性相关检验、加权残差Score检验、三次样条函数法。因篇幅所限，在此仅介绍COX-KM生存曲线和基于累计风险函数的图示法，对其他方法感兴趣的读者可参阅文献［4-6］。

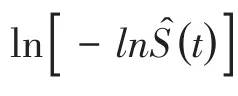
1.3 参数解释

Cox比例风险回归模型中偏回归系数βi的实际意义是：设δi代表第i个自变量在两个不同个体身上取值差量的绝对值，在其他自变量取值不变的条件下，变量δi每增加一个单位所引起的风险比的自然对数，即lnHRi=βi。

当βi＞ 0时，HRi＞ 1，说明Xi增加时，风险函数增加，Xi为危险因素（其真正含义是：此类因素取高水平相对于取低水平风险增大）；当βi＜0时，HRi＜ 1，说明Xi增加时，风险函数下降，Xi为保护因素（其真正含义是：此类因素取高水平相对于取低水平风险减少）；当βi=0时，HRi=1，说明Xi增加时，风险函数不变，Xi为对生存时间无影响的因素。

1.4 参数估计与假设检验

偏回归系数β1、β2、…、βp的估计需借助偏似然函数，用最大似然估计方法得到。偏似然函数的计算公式见式（3）：

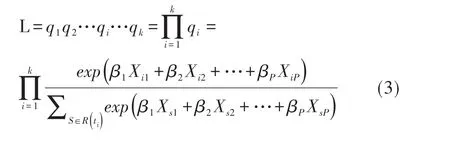
对偏似然函数取对数，得到对数偏似然函数lnL，求lnL关于βj(j=1，2，…，p)的一阶偏导数为0的解（通常需要采用非线性迭代算法，此处从略），便可获得βj的最大似然估计值bj。

假设检验方法类似于logistic回归分析，有似然比检验、Wald检验和Score检验，详细理论此处从略；使用统计软件计算时，参数估计与假设检验都可方便地实现。

2 实例分析

2.1 问题与数据结构

【例1】30例膀胱肿瘤患者生存资料原始记录见表1。研究者欲分析影响膀胱肿瘤患者生存时间（月）长短的因素，包括年龄、肿瘤分级、肿瘤大小和是否复发，并根据影响因素的取值对不同患者的生存情况进行预测。

表1 30例膀胱肿瘤患者生存资料原始记录

表1记录了30例膀胱肿瘤患者的年龄、肿瘤分级、肿瘤大小和是否复发等情况。其中，年龄和生存时间是定量变量，肿瘤分级、肿瘤大小、是否复发和生存结局是定性变量。由于存在截尾数据、生存时间及生存结局，且涉及到多个影响因素，所以，此资料为多因素影响下的一元生存资料。具体地说，生存时间为定量结果变量、生存结局为定性结果变量，它们的信息将被整合在一起参与Cox比例风险模型的建模；而其他变量都属于自变量或影响因素，其中年龄为定量自变量、肿瘤分级为多值有序自变量、肿瘤大小和是否复发为二值自变量。

2.2 创建SAS数据集

创建一个名为“tjfx”的临时数据集，数据步程序如下：

【SAS数据步程序说明】因篇幅所限，此处仅列出部分观测。详细数据见表1。

2.3 利用SAS/STAT中LIFETEST过程绘制生存曲线

该资料中年龄为定量变量，将年龄转化为二分类变量（＜60岁和≥60岁），分别按年龄、肿瘤分级、肿瘤大小和是否复发这四个变量的水平分组，采用Kaplan-Meier法绘制生存曲线，程序如下：

【SAS程序说明】生存曲线可用lifetest过程绘制，method用于指定计算生存率的方法，PL表示生存率的乘积极限估计法，即Kaplan-Meier法，plots=（s）用于绘制生存曲线；time语句为lifetest过程的必需语句，设置生存时间变量和生存结局变量，括号内为截尾变量的标示值；strata语句用于指定分层变量。

【SAS主要输出结果】

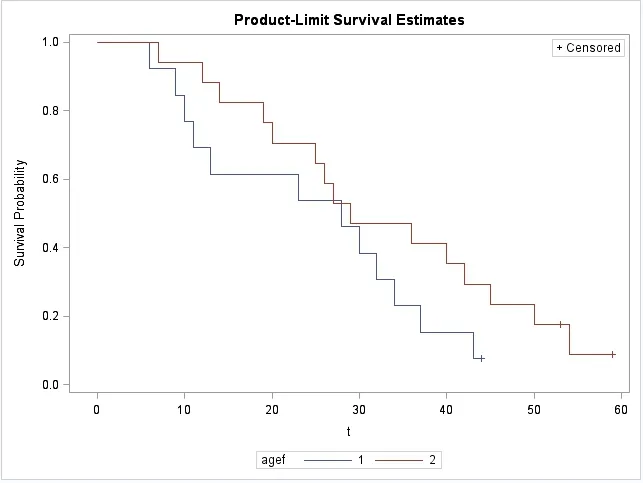
图1 年龄各水平下的生存曲线

图2 肿瘤分级各水平下的生存曲线

图3 肿瘤大小各水平下的生存曲线

图4 是否复发的生存曲线

以上四图显示，除两年龄组生存曲线在近30月处略有交叉外，其余各图中曲线均基本无交叉，说明四个变量基本满足PH假定，可以进行Cox比例风险回归模型分析。

2.4 利用SAS/STAT中PHREG过程拟合Cox比例风险回归模型

利用以下SAS程序，拟合Cox比例风险回归模型，计算每位患者的预后指数pi及其所对应生存时间的生存率。

【SAS程序说明】phreg过程是实现Cox模型回归分析的标准过程，其中class语句可以为分类变量设置哑变量，ref=选项用来指定参考水平，这里需注意的是：肿瘤分级为有序多分类变量，不同的肿瘤分级之间并非是严格的等距关系，因此也将其转化为哑变量进行量化；model语句是必需语句，等号左边为生存时间和生存结局变量（括号内为截尾标识），右边为协变量（即自变量），其中选项selection=forward|backward|stepwise|none|score用来指定变量筛选的方法，分别表示前进法、后退法、逐步法、全回归模型和最优子集法，sle=和sls=分别指定引入和剔除自变量的显著性水平，rl用来指定输出风险比hr的100(1-α)%置信限；程序中output语句创建一个新的SAS数据集report，含有为每一个观测计算的一些统计量，SAS为每一个统计量定义一个关键字，如生存率和预后指数分别用survival和xbeta表示。选项order=data规定输出的数据集中的观测顺序与输入数据集中的顺序一致。

【SAS主要输出结果及解释】

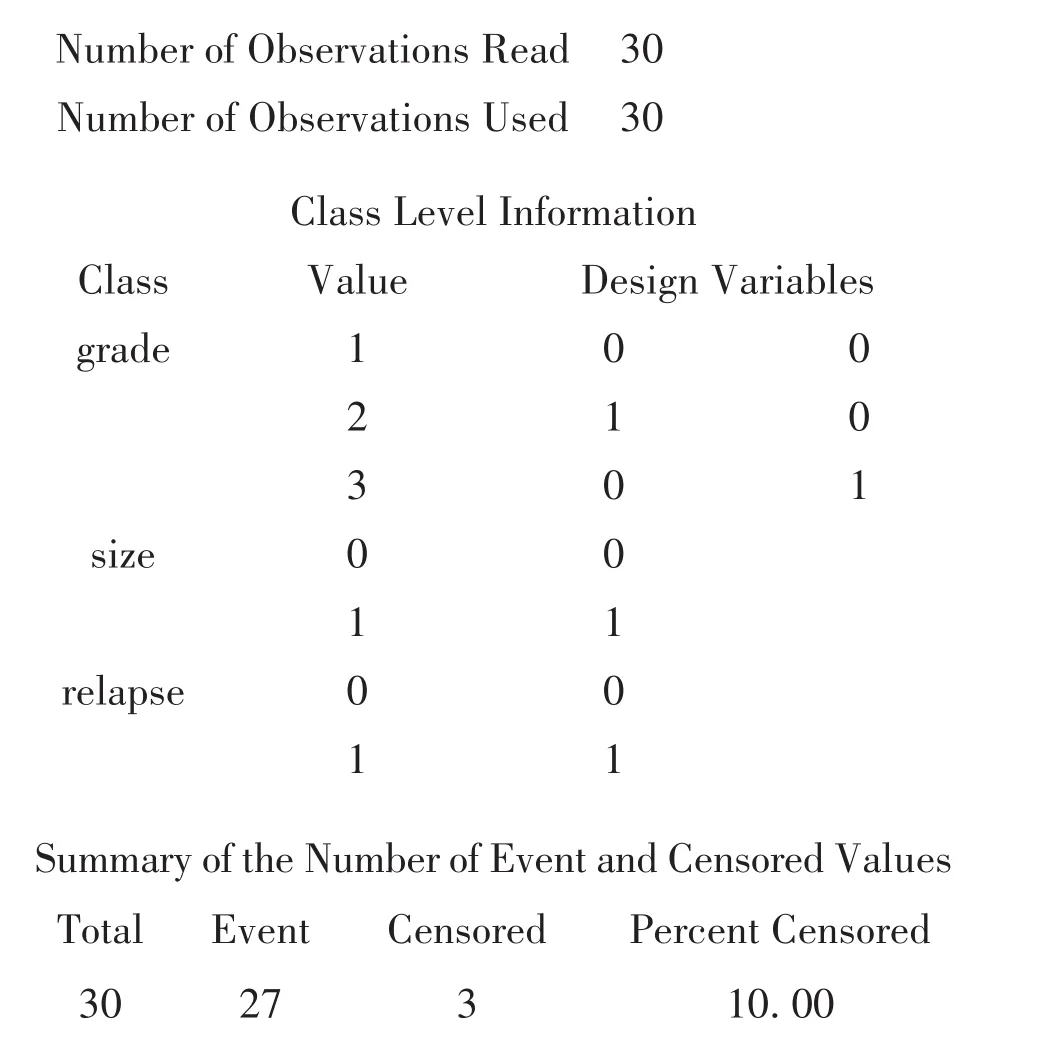
以上是模型的基本信息、分类变量的分类水平信息以及生存结局信息。

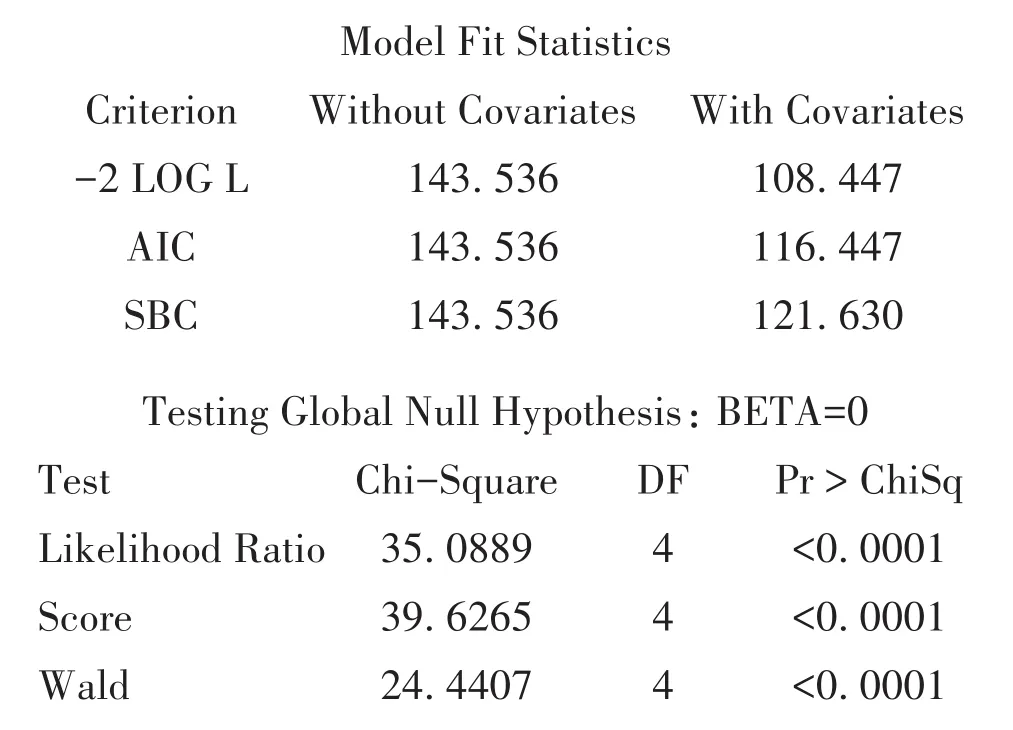
以上是经逐步回归后，用最终保留下来的协变量建立回归模型计算出的模型拟合统计量及模型检验结果，结果表明模型成立，即因变量与自变量之间的关系可以用所建立的回归方程来表示。

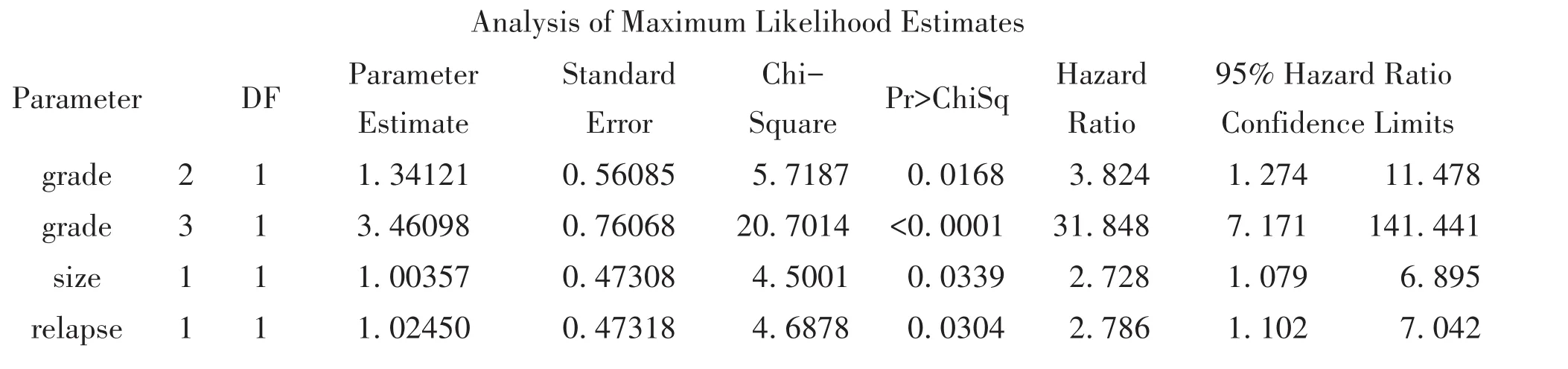
以上是模型的最大似然估计结果，包括参数估计值、估计值标准误、Waldχ2值、P值、风险比HR及其95%置信区间。由似然估计结果得出风险函数的表达式为：

Cox回归模型计算结果显示：肿瘤分级、肿瘤大小和是否复发为膀胱肿瘤患者生存时间长短的重要影响因素。在肿瘤大小和是否复发保持不变的情形下，II级肿瘤患者死亡风险是I级肿瘤患者死亡风险的3.824倍（e1.34121），III级肿瘤患者死亡风险是I级肿瘤患者的31.848倍（e3.46098）；在肿瘤分级和是否复发保持不变的情形下，肿瘤大于或等于3.0 cm者死亡风险是肿瘤小于3.0 cm者死亡风险的2.728倍（e1.00357）；在肿瘤分级和肿瘤大小保持不变的情形下，肿瘤复发者死亡风险是未复发者死亡风险的2.786倍（e1.02450）。

风险函数表达式右边变量的线性组合部分与风险函数成正比，其取值越大，风险越大，反映了一个个体的预后情况，称为预后指数（prognostic index，PI），其值越大，则风险函数h(t)的取值就越大，预后越差。此案例的预后指数为：

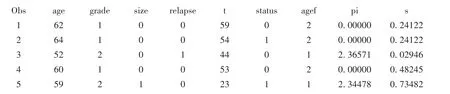
以上是report数据集中的内容，包括患者的基本信息、预后指数及其对应生存时间的生存率（由于篇幅限制，此处仅给出前5例患者的信息）。对于1号患者，肿瘤分级I级，肿瘤小于3.0 cm，未复发，其预后指数为0，59个月的生存率为24.12%。

3 讨论与小结

3.1 讨论

相对于非参数和参数回归模型而言，半参数回归模型兼有两者的优点，且不要求资料服从特定的概率分布，具有灵活性和稳健性，而且现如今还没有非常精准的方法判定待分析的生存资料中的生存时间服从何种分布，使得Cox比例风险回归模型在医学随访研究中得到广泛的应用。虽然Cox比例风险回归模型的适用范围广，但它依赖于严格的PH假定，若资料不满足PH假定，则会较大程度上影响计算的结果，甚至导致错误的结论。因此，在统计分析前，对PH假定的检验是重要且必须的。

3.2 小结

本文比较详细地介绍了Cox比例风险回归模型、构建模型需要满足的PH假定及其判定方法，并通过一个实例，基于SAS软件实现了Cox比例风险回归模型的构建、校正混杂因素后的组间比较以及对每个个体进行预后指数和生存率的预测。在进行Cox回归建模时，需注意只有满足PH假定前提下，基于此模型的分析预测才是可靠有效的。其次，还应注意回归所需样本含量的问题，经验估算方法是至少需要相当于协变量个数10～15倍的阳性结局事件数，或者根据Hsieh和Lavori给出的样本量估算公式进行计算，详细信息可参阅文献［7］。