基于广义互熵主元分析的故障检测方法
梁 艳,张彦云,巩明月,任密蜂,程 兰
(太原理工大学 电气与动力工程学院,太原 030024)
随着国民经济的飞速发展,人们对工业产品的需求不断增长,促使设备朝着多功能、大规模、结构复杂化和自动化的方向发展。然而,这种发展也带来了一些弊端:当过程装置发生故障时,不仅会因设备损坏,产品停产而造成严重的经济损失,还可能会因为危害人民的生命财产安全,污染环境,造成严重的社会问题。因此,为了及早发现潜在的故障,以确保足够的故障恢复时间,保证产品的生产质量,要对整个生产过程进行监控[1-2]。其中,将多变量统计过程监测(multivariate statistical process monitoring, MSPM)技术用于对多种化工过程进行故障检测取得了巨大成功。MSPM技术可以被视为数据科学在化工业中的应用,它能够从大量的常规过程数据中挖掘出有价值的信息,大大提高了可靠性和效率[3-4]。在这些MSPM技术中,主元分析(principal component analysis,PCA)是最受欢迎的方法之一[5-8]。
典型的MSPM数据模型以维度减少过程开始,该过程提供潜在的数据结构。以PCA模型为例,在建立PCA模型之后生成主元子空间和残差子空间。然后,相应的统计信息T2统计量和SPE统计量可用于每个子空间中的过程监控[9-10]。传统的PCA方法是用欧几里德距离来测量PCA中的重构误差,文献[11-14]提出用新的度量——L1范数,替换先前的欧几里德距离来进行计算。在文献[14-15]中,通过极大似然估计建立L1范数PCA,然后分别获得L1范数的启发式估计和替代凸规划来求解最小化重构误差问题。但是这些都依赖于该过程在理想条件下操作并且数据服从高斯分布的假设。然而,由于实际过程中的非线性特性,即使扰动服从高斯分布,过程输出数据也可能是非高斯的[10],这使得PCA模型不能有效地发挥作用并导致检测结果不准确。
为解决上述问题,文献[16]提出一种独立成分分析(independent component analysis,ICA)的方法,以寻找具有非高斯性的变量的线性组合。通常,ICA模型更能有效地提取非高斯分布数据的基本信息,且ICA中的主成分在非高斯分布下是独立的[17-18]。但是IC数量一般依据经验进行选择,没有一定的理论支持,并且在实际过程中,如果多于一个分量是高斯分量,则ICA算法可能不会收敛[19]。为了避免使用ICA算法可能会出现的一些弊端,信息理论学习(information theory learning,ITL)中一些可以描述非高斯随机特性的度量(如,熵,互熵等)被用于改进PCA[20-21,28]。文献[22]提出了一种最大熵PCA算法(maximum entropy PCA,MaxEnt-PCA),其目标是寻找一个投影矩阵使得数据经PCA投影后的方差最大。文献[23]则从重构误差的角度出发,提出了基于最大互熵的PCA算法,令重构误差与和零之间的互熵最大,从而降低误差在零附近的随机性。互熵中默认的核函数是高斯核,但是,它并不总是最佳选择。因此,一个更具一般性的互熵——广义互熵(generalized correntropy,GC)被提出来。
本文将广义互熵用于PCA(generalized correntropy PCA,GC-PCA)以进行非高斯系统的故障检测。互熵是使用来自高阶信号统计特性的信息来测量两个随机变量广义相似性的一种度量[25]。广义互熵具有使用高斯核的原始互熵的优点[25-27]:1) 它包含所有的偶数阶矩,且高阶矩的权值仅由核的大小决定;2) 对任意分布都有界;3) 它是一种局部相似性度量,对异常值很稳健。同时,它还具备传统互熵不具备的优点[24]:1) 广义互熵是对称的;2) 广义互熵涉及误差变量的高阶绝对矩。本文所提出的GC-PCA是将传统PCA中的均方误差(mean square error,MSE)准则用GC准则进行替代,以处理重构误差的非高斯特性。
1 主成分分析算法
给定一个样本数据集Z=[z1,z2,…,zn],其中,zi是维度为d的变量;U=[u1,u2,…,um]∈Rd×m是正交投影矩阵;V=[v1,v2,…,vn]∈Rm×n为投影矩阵U下的投影坐标。基于最小重构误差准则,PCA可定义为如下的优化问题:
(1)
式中:‖·‖代表L2范数;μ是矩阵Z的中心。因为(1)式基于L2范数,所以这种PCA被定义为L2-PCA。由投影理论可知[29],当U固定时,使(2)式最小化的V满足等式V=UTZ.
由于L2-PCA方法本质上是以二阶MSE标准为指标的线性变换技术,如果高维过程数据中包含有非高斯信息,采用该方法不能有效地对数据进行降维压缩和成分提取。因此,本文提出使用广义互熵来描述数据的非高斯特性。
2 广义互熵PCA算法
2.1 广义互熵标准
互熵是一种局部相似性度量,与两个随机变量在由核宽控制的联合空间邻域中的相似程度直接相关[30]。给定两个随机变量X和Y,互熵定义为:
Vσ(X,Y)=E[κσ(X-Y)] .
(2)
式中:E[·]代表期望,κσ是核宽为σ的核函数。一般选择高斯核作为互熵的核函数:
(3)
然而,高斯内核并不总是最佳选择[31]。在接下来的工作中,使用广义高斯密度(generalized gaussian density,GGD)函数作为互熵中的核函数,称为广义互熵(generalied correntropy,GC),定义为:
Vα,β(X,Y)=E[Gα,β(EX-Y)]=E[Gα,β(X-Y)] .
(4)
在这里,
(5)
式中:Γ(g)为伽玛函数;α>0为形状参数;β>0是带宽参数;λ=1/βα是核参数;γα,β=α/(2βΓ(1/α))是归一化常数。其中,α=2时的广义互熵与具有高斯核的互熵相等。
若随机变量X和Y的联合概率密度函数f(x,y)已知,则互熵可由下式进行计算:
(6)

(7)
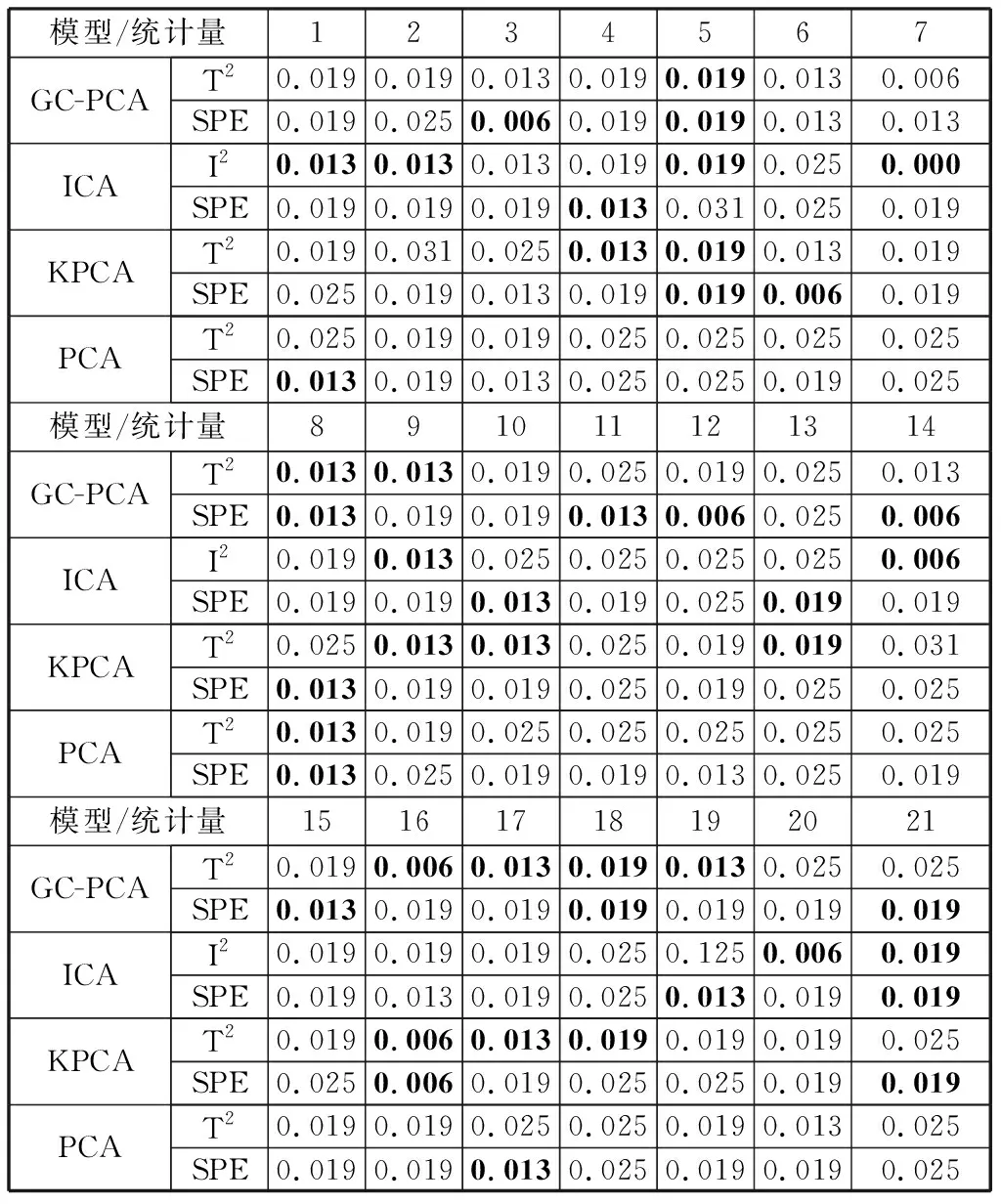
值得注意的是,广义互熵为正并且有边界:0 将x(i)=Zi和y(i)=μ+Uvi带入(7)式,则广义互熵主元分析可以通过最小化以下GC损失(GC-loss)函数来解决: JGC-loss(X,Y)=Gα,β(0)-Vα,β(X,Y)=γα,β(1-E[Gα,β (8) 其中, (9) 首先,使用拉格朗日乘子法将以上带约束的最大化问题转化为无约束问题,如下所示: JH=JGC-loss(X,Y)+TrΛ(UTU-I) . (10) 式中,Tr(·)是矩阵的迹;Λ是拉格朗日系数。 然后,使用梯度下降法对上式进行求解: (11) 式中,μ和η为学习率。 (12) (13) 图1 T2和SPE统计量的概率密度分布图Fig.1 Probability density distribution of T2 and SPE statistics (14) (15) 其中,Gα,β表达式在(5)中给出。 从图1可以看出,曲线和X轴包围的面积等于1,我们可以通过设置置信度为α的统计阈值来确定控制限。控制限LT2和LSPE的计算如下式所示: (16) (17) 这里将所提出的算法用于TE过程进行故障检测。整个TE工艺由五个操作单元组成:反应器,气液分离器,循环压缩机,产物冷凝器和汽提塔。气态反应物进入反应器,在气相催化剂的催化下,生产出气态产品和液态副产品。反应过程中产生的热量经内置冷凝物包而去除。反应过程结束后,一些未反应的物质和催化剂仍保留在反应器中[31]。 TE生产过程主要由A、C、D和E四种气态物料参与反应,生产出两种气态产品G、H和一个液态副产品F.此外,在生产过程中,还会有少量的惰性气体B参与[31]。该过程主要由以下反应方程式描述的四个反应过程组成: A(g)+C(g)+D(g)→G(g),Product; 该过程有12个控制变量和41个测量变量,因为变量个数较多,本文通过交叉验证法选取了其中的16个过程变量,这些变量可以准确描述TE过程的运行状况,如图2所示。 图2 交叉验证结果图Fig.2 Cross validation result TE过程可以模拟不同的故障模式,包括一些过程变量的阶跃变化和随机变化,以及粘滞阀,这对于测试故障检测方法很有意义。表1给出了TE过程对21种过程故障的描述。本节先使用训练数据(包含500次采样)建立模型;然后,使用故障数据集进行故障诊断,故障数据包含960个样本,每种故障发生时间从161个样本点持续到960个样本点。 表1 TE过程故障列表Table 1 TE process failure list 首先,使用来自数据集的正常样本构建每个统计监测模型:①对正常样本进行标准化处理;②构建GC-PCA,ICA,KPCA和PCA模型求取投影矩阵;③利用交叉验证法选取主元个数;④计算正常数据的T2和SPE统计量的值;⑤通过核密度估计法确定T2和SPE的控制限。然后,对21种故障样本集进行故障检测:①对故障样本进行标准化处理;②利用建模过程求得的投影矩阵计算故障数据的T2和SPE统计量的值;③检测T2和SPE统计量的值是否超过正常条件下计算的T2和SPE的控制限,如果超过该控制限,表明系统发生了故障。21种故障进行检测的漏报率和误报率列于表2和表3中。可以看出,对于在大多数故障,GC-PCA方法都给出了非常优越的检测结果,即故障检测的漏报率和误报率比较低,以粗体标记。 表2 故障检测漏报率Table 2 Failure detection missed detection rate % 表3 故障检测误报率Table 3 Failure detection false alarm rate % 为了直观反映算法的优越性,图3、图4和图5分别给出了故障4、故障7和故障20的检测结果图。对于故障4,可以看出KPCA算法和PCA算法都无法检测出故障发生,GC-PCA的T2统计量虽然漏报率有一些高,但其SPE统计量完美的检测出了故障,此时,ICA算法表现出良好的故障检测能力。针对故障7,在故障持续发生的时间段内,GC-PCA和ICA对故障的持续检测能力最好,其他两种算法在故障后半段已经无法检测出故障。最后,对于故障20,三种方法都可以检测出故障,其漏报率平均为35%、35.9%、68.5%和72%,证明了所有算法的优越性。虽然GC-PCA和ICA针对非高斯数据都表现出优秀的检测能力,但是ICA算法本身只能处理纯非高斯数据,若过程变量不都服从非高斯分布,使用ICA算法会无法收敛,而GC-PCA算法则不需考虑这一问题。 图5 故障20检测结果Fig.5 Failure 20 detection results 本文从重构误差的角度出发,将广义互熵准则引入传统PCA方法,用于非高斯噪声下的系统故障检测,并将该方法应用于TE过程进行仿真验证。通过仿真可以看出,在非高斯噪声的影响下,ICA方法、PCA方法和KPCA方法故障检测的及时性不足,漏报率较高。而本文所提出的广义互熵PCA方法可在最大程度消除非高斯的影响,有效提高了分析与诊断过程变化的能力,表现出良好的故障检测能力。在未来的工作中,可以将所提出的方法扩展到输入或干扰表现出严重动力学的系统,以解决更多的故障检测问题。2.2 广义互熵PCA
(X-Y)])=γα,β=(1-E[exp(-λ|X-Y|α)]) .
3 故障检测指标
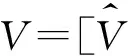

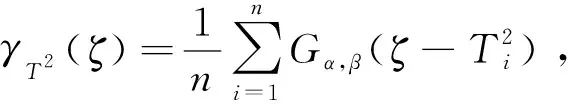

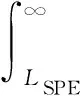
4 仿真分析
A(g)+C(g)+E(g)→H(g),Product;
A(g)+E(g)→F(lip),Byproduct;
3D(g)→2F(lip),Byproduct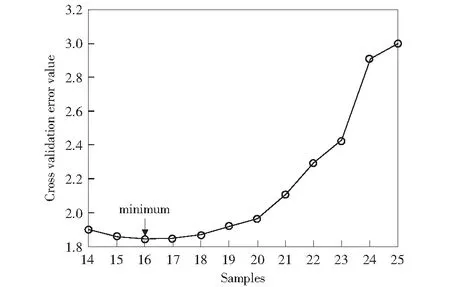



5 结束语

