以“构建数学模型”为核心，培养学生核心素养——以《乘法分配律》一课为例

文/华南师范大学附属惠阳学校

模型思想是一种数学的基本思想，是学生体会和理解数学与外部世界联系的基本途径通过数学建模建立数学与外界联系是当前课程改革形成的共识。本文以《乘法分配律》一课为例，探讨构建数学模型的路径，培养学生核心素养。

一、巧用几何直观感知模型，培养直观想象素养

要想使学生有效建构模型，首先要引导学生从生活原型中感知模型。即把数学问题借助情境以图案方式表达出来，实现由实物到几何图案的转变。学生在借助几何直观和空间想象的过程中，培养直观想象素养。

教学《乘法分配律》时，先出示情境图，鼓励学生根据图意用多种方法解答“贴了多少块瓷砖？”有的学生横向观察，从颜色角度先算出白色和蓝色瓷砖的数量再算出总块数：3×10+5×10=80(块)；还有的学生直接把白色和蓝色合成一个大长方形，先算出宽的和再算出总块数：(3+5)×10=80(块)。也有的学生纵向观察，求出左、右两面墙的块数再得出总块数：4×8+6×8=80(块)；或者把左、右两面墙合成一个大长方形，先算出总长再算出总块数：(4+6)×8=80(块)。因为数值相等和数字特点，学生很容易发现这样的等式：3×10+5×10=(3+5)×10，4×8+6×8=(4+6)×8，并仿写出许多同类型的等式。从图到建立关系形成等式，再到仿写等式的过程，其实就是感知模型的过程。

二、运用类比推理建立模型，培养数学抽象素养

具有一定的推理能力是培养学生数学素养的重要内容。

当学生对乘法分配律有了初步感知后，我尝试引导学生从数与形、数量关系与图形关系中抽象出数学知识及一般规律和结构，并用数学语言予以表征。有的学生用文字表达，还有的学生用符号表达。绝大部分学生因为在前面学习中积累了用字母表示规律的经验，所以建立起这种表达方式：a×c+b×c=(a+b)×c。有了这样的模型，我再顺水推舟告诉学生乘法分配律的另一种表达形式(a+b)×c=a×c+b×c就是水到渠成的事情。

在这环节里，学生进行分析、比较、抽象和概括的思维活动，揭示了知识内涵及相互关系，经历了从具体数值到符号表达的过程，实现了从“境”到“模”的转化，数学抽象素养得到培养。

三、借助思辨思维验证模型，培养逻辑推理素养

“学起于思，思源于疑”。思维总是由问题引起的。学生在分析问题中不断反思、验证猜想的过程中掌握数学知识结构，提高各种思维能力。

调查发现，不少老师在学生建立公式模型后忽略了对模型的验证。所以我会问：(a+b)×c=a×c+b×c左右两边为什么会相等呢？有的学生从乘法意义的角度去解释：(a+b)×c是求(a+b)个c，而a×c+b×c则是求a个c连加，再加上b个c连加。所以(a+b)×c其实就是a×c+b×c。也有学生从几何直观的角度去理解：

如图1，长方形1的面积是a×c，长方形2的面积是b×c，大长方形的面积是(a+b)×c，那么大长方形的面积就是长方形1的面积加长方形2的面积，即(a+b)×c=a×c+b×c。还有的学生利用前面学习过的点子图个性化地解释乘法分配律(见图2)。

图1

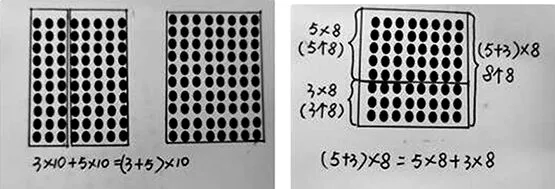
图2

学生借助推理、方块图、点子图，形象直观地解释了自己对算理的理解，验证了数学的模型，培养了学生数学抽象素养。

四、利用应用意识应用模型，培养数学运算素养

数学应用意识是一种用数学的眼光、数学的思维观察、分析问题的思维反应。

因此在课的最后，我尝试让学生根据乘法竖式计算的过程说说它与乘法分配律的关系；再根据乘法分配律是竖式乘法的依据，挑战四年级下册才学习的小数乘法2.1×4的计算结果；最后根据乘法分配律“说一说”欧洲人的“双倍法”。

众所周知，乘法分配律作为一种运算定律，其最大的作用就是提高计算速度与准确率。不仅如此，学生在运用运算定律解决数学问题的过程中，表现出来的选择运算方法、设计运算程序、求得运算结果等则是培养了数学运算素养。