基于磁力固定的PCB载具抗贴偏性研究

黄 超, 茅 健, 周玉凤

(上海工程技术大学 机械与汽车工程学院, 上海 201620)

表面贴装技术(Surface Mount Technology,SMT)是当前电子产品制造业中使用最为广泛的组装技术[1].SMT生产线主要由贴片机、自动光学检测(Automated Optical Inspection,AOI)设备、焊锡印刷机、点胶设备、回流焊炉等构成,适用于大批量生产小体积、高性能的电子产品,如智能手机、固态硬盘、笔记本电脑等.SMT中贴片机专用于将电子元器件准确贴装在印制电路板(Printed Circuit Board,PCB)的预定位置,为防止PCB在贴装过程中发生偏移导致报废,须将PCB固定在相应夹具装置上[2].但现有贴片机专用夹具只适应特定规格PCB的贴片加工[3],当PCB尺寸变动范围较大时,专用夹具不再适用,须频繁更换夹具.

为解决PCB固定这一问题,国内不少单位研制高适应度自动贴片机,主要针对贴片机夹具进行结构改造.珠海祺力电子有限公司唐换名[4]研发一种既能夹持矩形形状PCB,又能夹持不规则形状PCB的贴片机夹具,主要通过两组滑动卡件包覆在PCB边缘以实现固定.李继昌[5]针对螺钉固定PCB后不便于拆卸的缺点,研发一种仅需松紧螺母便可固定和移动不同尺寸PCB的贴片机夹具.肖海等[6]针对贴片机只装有单个夹具影响贴片效率的问题,研发一种三段式贴片机夹具,该夹具可同时容纳3个夹具,可提高更换夹具的速率.本文针对PCB固定问题,从理论上分析磁铁吸附固定的可行性,提出磁力计算模型,采用有限元法进行磁力仿真求解,提出通过磁力固定PCB的方案.

1 磁力计算理论

设面积为2a×2b的矩形磁面如图1所示.

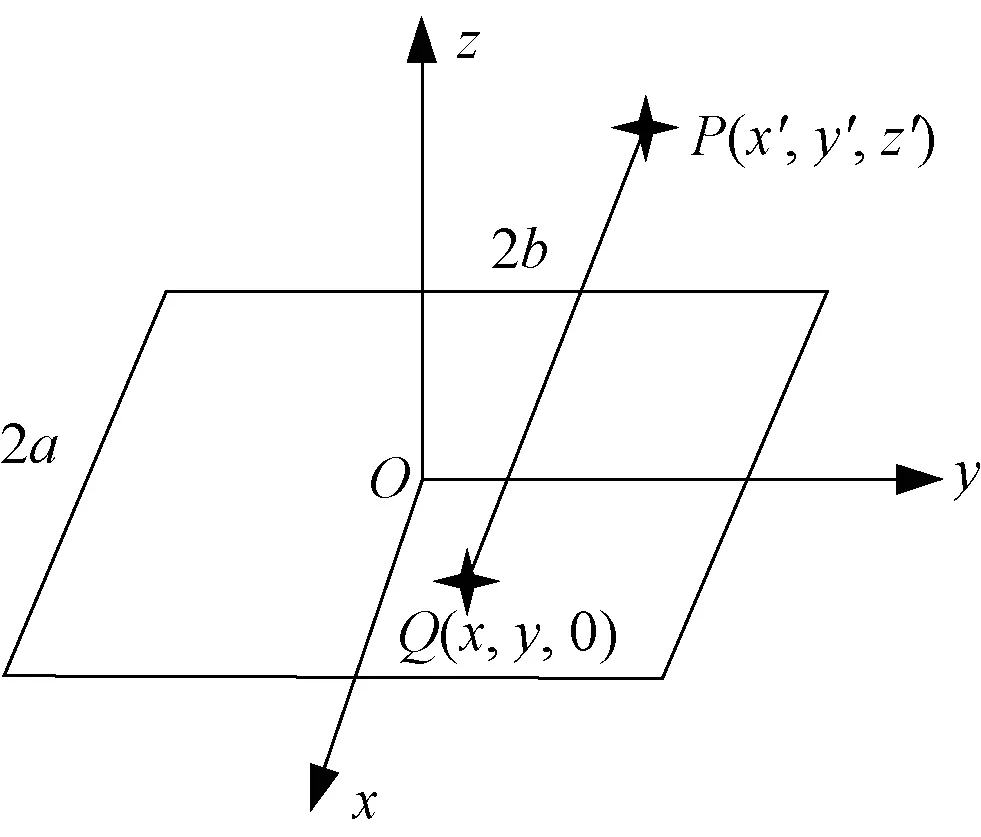
图1 P点磁标量势Fig.1 Magnetic scalar potential at point P

依据等效磁荷理论[7],任意一点P的标量磁位方程为

(1)

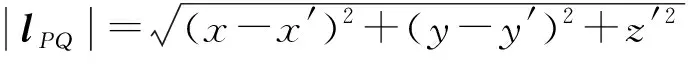
(2)

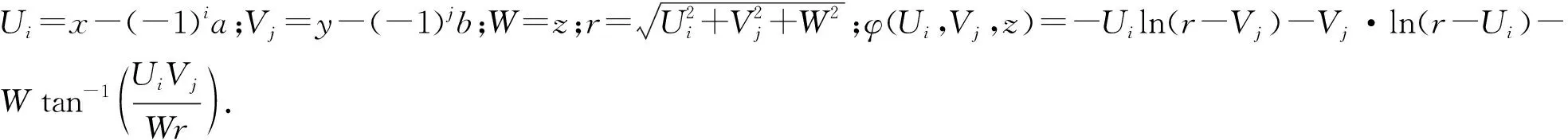
对于体积为2a×2b×2c的矩形磁铁,被磁化后只在两端面上出现正或负磁荷.假设充磁方向与磁铁表面法线方向重合,由静磁学理论[8]在点P处对φp求梯度,可得P点处磁场强度为

(3)

其中

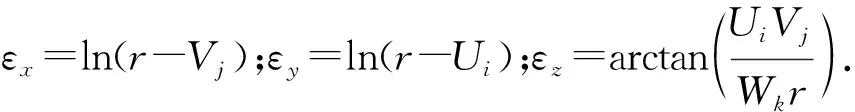
将两块矩形磁铁上下放置,如图2所示.上方磁铁A:介质极化强度为J,体积为2a×2b×2c;下方磁铁B:介质极化强度为J′,体积为2a′×2b′×2c′,充磁方向互相平行.

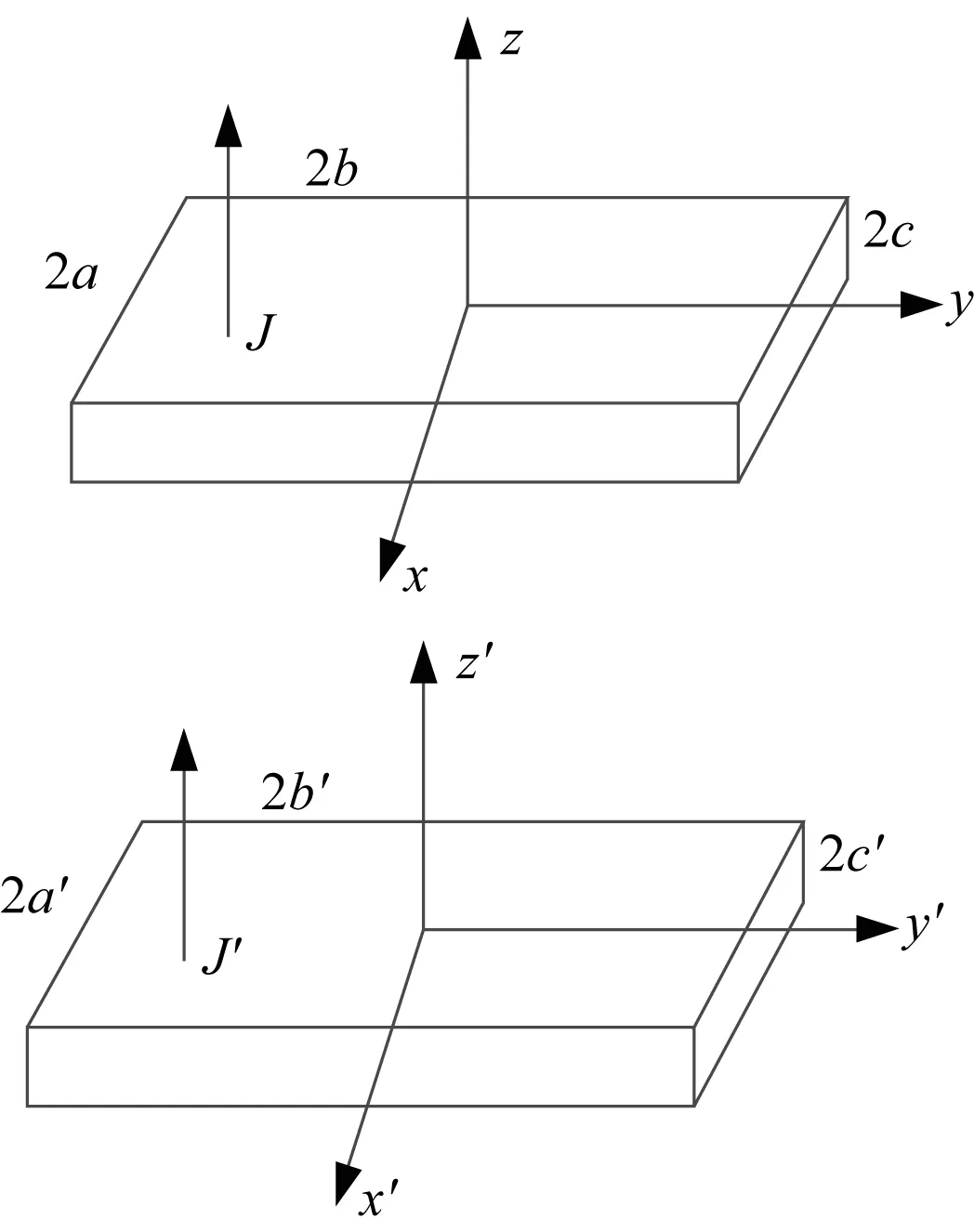
图2 矩形磁铁计算模型Fig.2 Rectangular magnet calculation model

根据等效磁荷理论,两块磁铁间的磁力由相对的两个端面相互作用产生,静磁能[9]计算式为

(4)

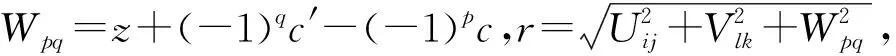
ψ(Uij,Vkl,Wpq,r)

(5)

其中

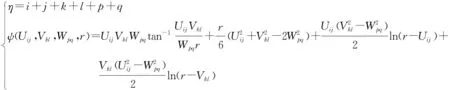
(6)

根据虚功原理[8]得两块矩形磁铁间磁力,当上下磁铁充磁方向相同时F取正,反之取负[10],计算式为

(7)

其中

带磁性PCB载具实物如图3所示.将两根带磁性的压条分别置于载具上下端的两个小凹槽中,载具上有定位销孔.

图3 带磁条载具Fig.3 Carrier with magnetic stripe

载具初始状态如图4所示.磁条未固定PCB,磁条吸附在载具表面固定,如图5所示.

图4 初始状态Fig.4 Initial state

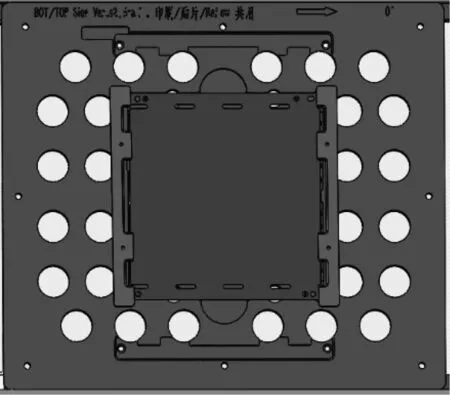
图5 固定PCBFig.5 Fixing PCB

PCB固定后,将磁条与载具表面接触部分抽离出来构成简化的计算模型,如图6所示.磁条材料选用导磁性较好的钕铁硼,几何参数见表1.

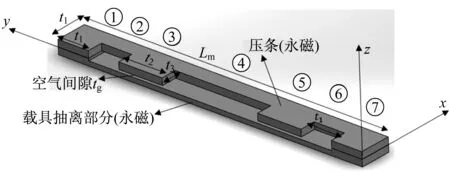
图6 磁力计算模型Fig.6 Magnetic calculation model

将模型划分为图6所示的7段矩形方块,各段几何参数见表2.将各段参数分别代入式(7)进行磁力求解,求和可得磁条吸附力F磁.

表1 磁条几何参数Table 1 Magnetic strip geometric parameters

表2 计算明细表Table 2 Calculation schedule

2 有限元模型

2.1 模型建立

利用ANSYS分析时使用的耦合场单元为SOLID98[11],共定义3种材料属性:材料1为压条永磁;材料2为载具永磁;材料3为空气.由于压条截面尺寸变化较大,对磁通密度分布影响较大,建模时将其划分为7个体单元,载具部分单独作为1个体单元.

加边界条件:在对称平面(z=0)内磁力线垂直通过,所以在这个位置施加磁力线垂直的边界条件(φ=0).由于假设不漏磁,所有磁通量沿磁路通过,故在所有其他外表面上施加磁力线平行的边界条件(∂φ/∂n=0).求解后,得到磁通密度矢量如图7所示,磁场强度矢量如图8所示.

2.2 仿真结果分析

1) 磁通密度在所选路径上的分布

在对称平面(z=0)内选取20个特征节点 (图7中1,2,3,…,20),依次连接相邻特征点形成路径Path,将磁通密度数据映射到路径Path上,得到磁通密度变化如图9所示.图中,两端节点磁通密度最大,中间节点由于存在空气介质,磁通密度骤减;此外,大截面处节点磁通密度大于小截面处节点磁通密度.

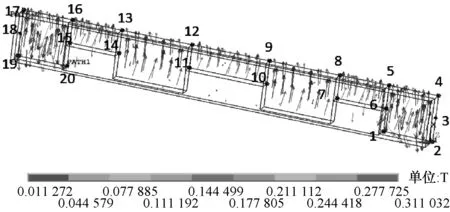
图7 磁通密度矢量图Fig.7 Vector diagram of magnetic flux density

图8 磁场强度矢量图Fig.8 Vector diagram of magnetic field strength

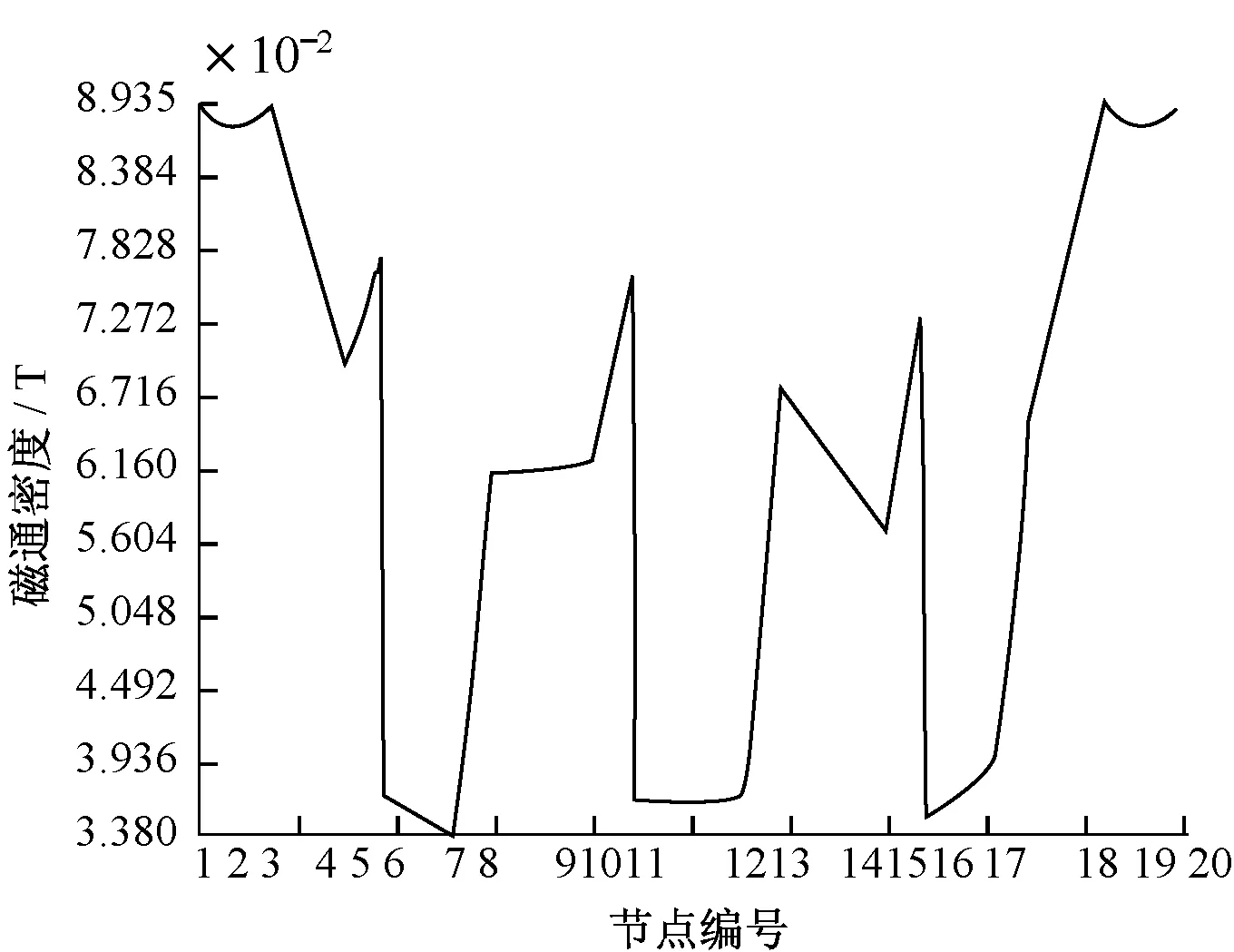
图9 路径Path上磁通密度Fig.9 Magnetic flux density on Path

2) 磁力在所选路径上的分布

将节点磁力数据映射到路径Path上,如图10所示.由图可见,节点磁力表现出与节点磁通密度相似的变化规律,由于空气介质对磁力分布的影响,导致即使是在对称节点,磁力也并非一定相等.

3 贴装试验仿真

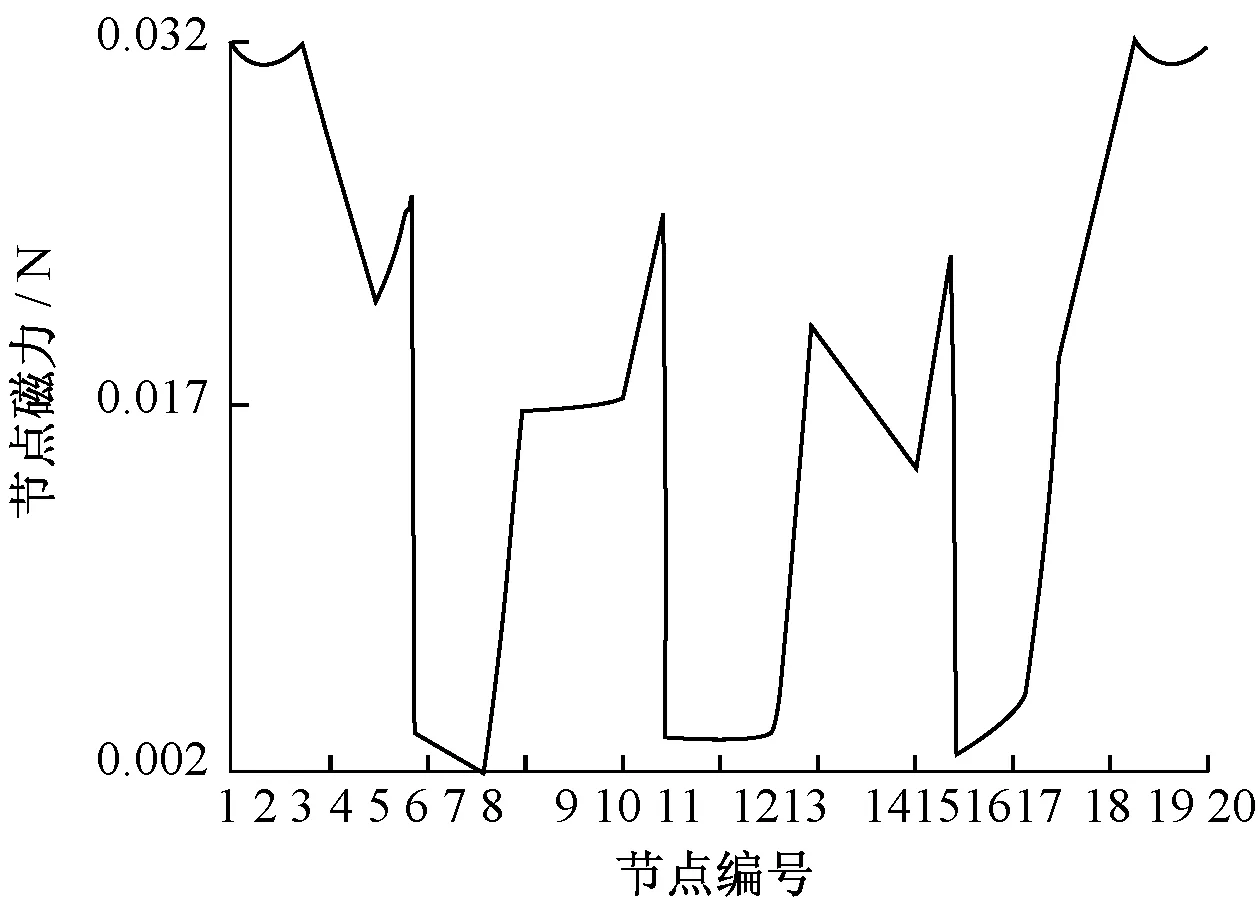
图10 Path上节点磁力变化曲线Fig.10 Magnetic variation curve of nodes on Path

1) 从同一高度3个不同位置下落小球,初始速度均为100 m/s.PCB板材料选用聚乙烯,小球材料选用结构钢,划分网格单元大小为0.005 m,将薄板两个端面固定,求解时间设定为0.5 s.3组试验小球位置如图11所示.1号落点应变如图12所示.3组测试应力分布图13所示.

从图12和13可以看出,当小球从靠近薄板中心区域(1号位置)下落时,对薄板两个端面几乎没有造成冲击,所以要验证σ磁是否满足约束条件,应尽量选取靠近薄板边缘的落点进行试验.2号位置下落时最大应力比3号位置大,σmax<0.08 kPa<σ磁,σ磁满足约束条件.

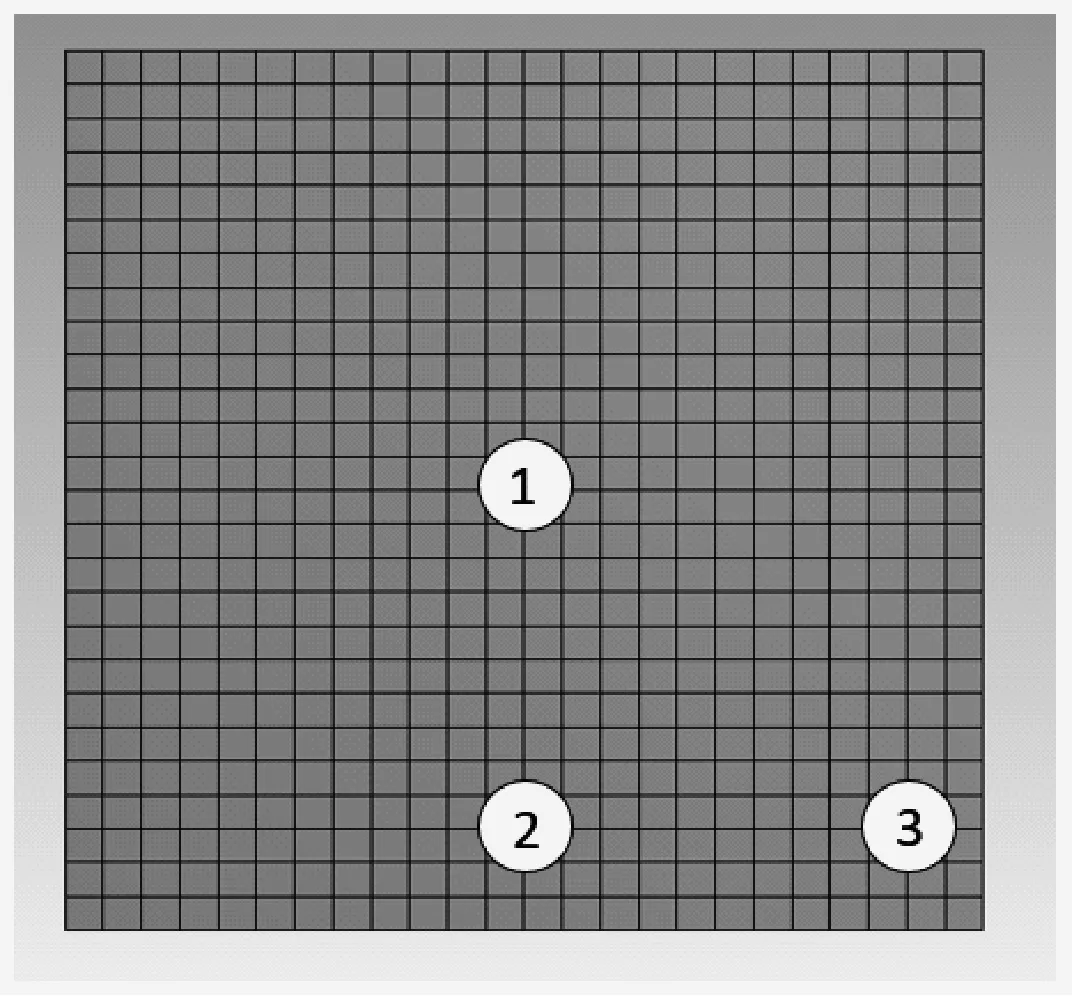
图11 落点位置Fig.11 Location of drop point

图12 1号高点应变测试Fig.12 Equivalent elastic strain test at positio one

图13 不同下落位置应力分布图Fig.13 Stress distribution diagram of different falling positions

2) 从同一位置以不同速度下落小球,取2号位置落点进行测试.让小球在2号位置,分别以初始速度v=100、110、120和130 m/s下落,应力分布如图14所示.由图可知,当小球初始速度增大时,薄板表面产生的碰撞应力逐渐增大;当v=130 m/s,t=0.5 s时,产生的最大应力σmax=0.192 kPa<σ磁,说明此时σ磁仍然满足约束条件.在实际贴装过程中,贴装头速度越大,产生的碰撞应力也越大.

4 真机试验

本文选择3种不同规格PCB进行真机试验. A组:PCB尺寸为120 mm×128 mm×1 mm,400片;B组:PCB尺寸为80 mm×100 mm×1 mm,400片;C组:PCB尺寸为150 mm×200 mm×1 mm,400片.贴片机型号为Panasonic-NPM-W2,如图15所示.

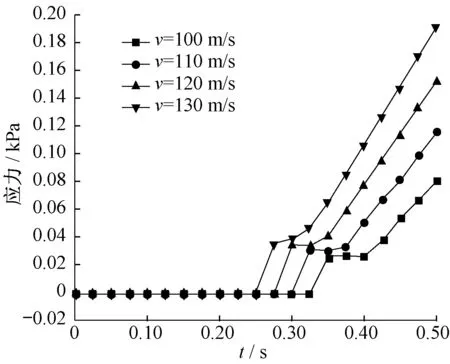
图14 不同下落速度应力分布图Fig.14 Stress distribution diagram of different falling speeds

图15 现场测试图Fig.15 Field testing diagram

第1组试验:将贴装头速度设定为100 m/s,安装好磁条;分别将A、B、C 3组各100片PCB投入贴装加工工序;贴装后利用AOI测量仪检测PCB偏移量.第2、3、4组分别将贴装头速度设定为110、120和130 m/s,其他条件保持不变.生产规定PCB的X和Y方向上偏移量不能超过0.1 mm.

统计分析1 200片PCB的X和Y方向上的偏移量,1 200片PCB可分为12组,每组100片,从每组中采用不放回随机抽样的方式取出3片,共抽取36片PCB作为样本,样本偏移量见表3.散点图如图16所示.由此可见,样本偏移量均处于生产允许范围内,并由样本推断出总体偏移量也均在允许范围内.实际生产结果表明,1 200片PCB偏移量均能满足生产要求,并未出现不合格品.

表3 12组样本偏移量Table 3 12 group sample offsets mm

图16 样本偏移量散点图Fig.16 Scatter diagram of sample offset

5 结 语

本文针对贴装过程中固定PCB的问题展开研究,提出可行的磁力载具方案.利用等效磁荷和静磁学理论中磁力计算公式,计算出磁条磁力大小后,经ANSYS进行磁力仿真,得到磁力仿真值与理论计算值.碰撞模拟试验和真机试验均证实磁力载具方案具有可行性.本文仿真过程中忽略温度对磁力的影响,但实际生产中载具进入120 ℃炉温机中进行回炉焊工序时,磁条磁力会产生一定波动.此外,贴装过程伴随着高频率振动,本文只是根据瞬时碰撞应力大小对磁力的约束进行校核,满足静力学条件,下一步工作是在动力学条件下进行研究.