方程式汽车车架性能分析与评价

李国竣

(西华大学 汽车与交通学院, 成都 610039)

中国大学生方程式汽车大赛(FSC)是由在校大学生参与的一项比赛,是让在校大学生自行设计制造一辆原型车,完成75 m直线加速、8字环绕、高速避障和耐久测试[1].车架是整个赛车各个总成的载体,车架性能优劣直接影响赛车性能好坏.

本文利用力平衡公式计算悬架作用在车架上的载荷,通过计算机仿真分析作用在车架上的载荷并判断车架是否满足设计要求.

1 车架几何模型建立及有限元前处理

1.1 车架几何模型建立

依据FSC规则[1],本文车架选用30CrMo合金钢圆形薄壁钢管,其弹性模量为211 GPa,泊松比为0.279,质量密度为7 850 kg/m3,屈服极限为785 MPa.

车架主体以三角形结构为主,在CATIA软件中利用肋功能建立车架模型并进行剖口处理,如图1所示.利用ANSYS Workbench软件CAD/CAE端口导入三维模型[2].在导入的三维模型中进行几何清理、布尔操作提取悬架和车架连接的各个硬点,如图2所示.

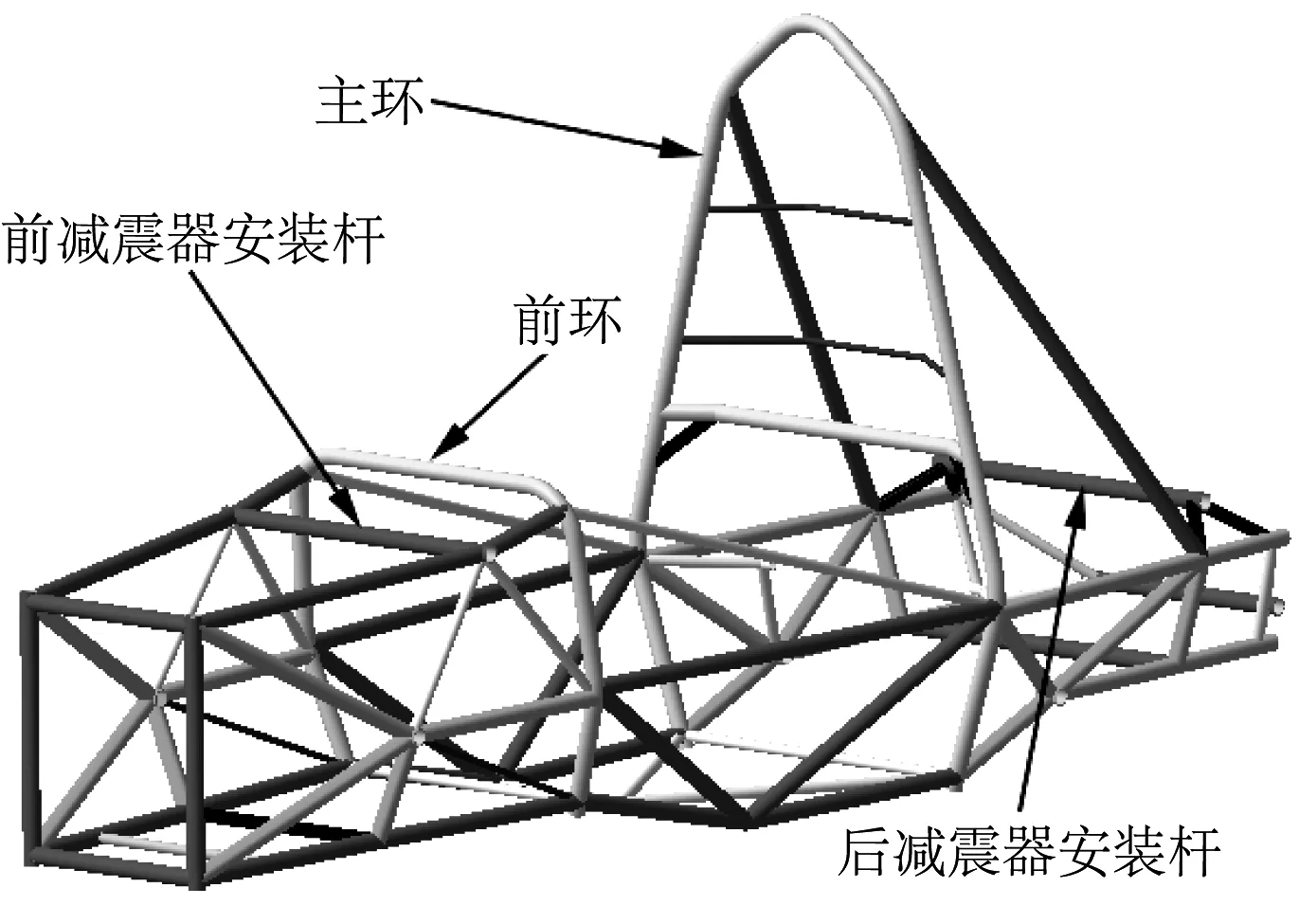
图1 FSC车架三维几何模型Fig.1 3D geometric model of FSC frame

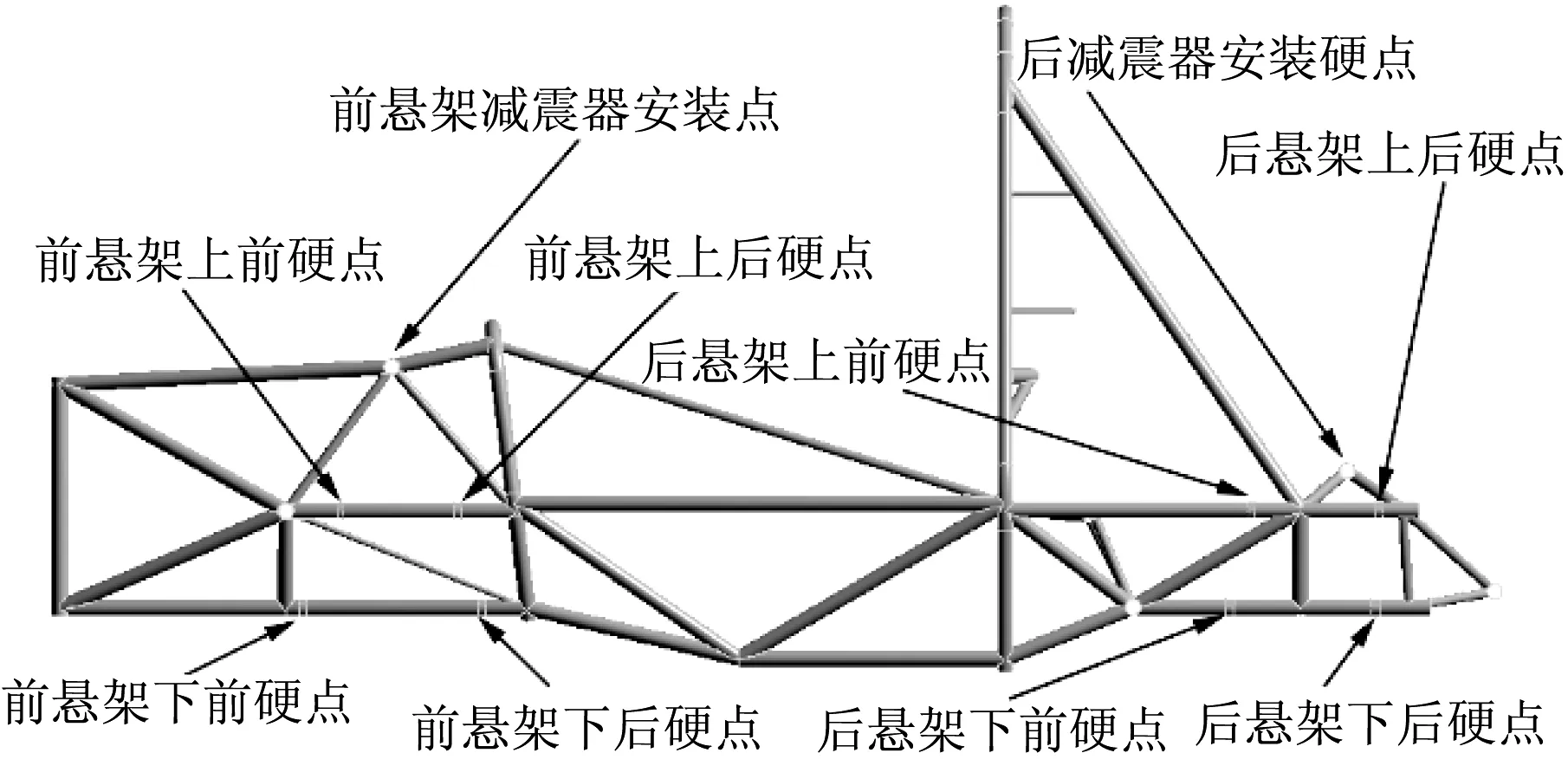
图2 悬架系统各个硬点位置Fig.2 Hard point positions of suspension system

ANSYS Workbench网格划分智能化程度很高,本文选用自动网格划分[3],设置关联度为60,尺寸功能设置Curvature,关联中心和关联角度为中等,设置网格尺寸增长率1.2,最大面尺寸10 mm.得到网格节点数量1 254 733,单元数目613 498.

2 车架边界条件处理

2.1 车架载荷

车架载荷主要包括发动机质量、车手体质量和悬架作用在车架上的集中载荷[4-5].本文发动机选用CBR600,质量约60 kg,取车手体质量78 kg.分别计算在制动、转弯和加速极限工况下悬架作用在车架吊耳上的集中载荷.悬架采用双横臂式独立悬架,上下横臂分别通过球铰与转向节相连,只要求出作用在这两个球铰上的力就可以知道各个零件受力.车架载荷计算所需参数见表1.

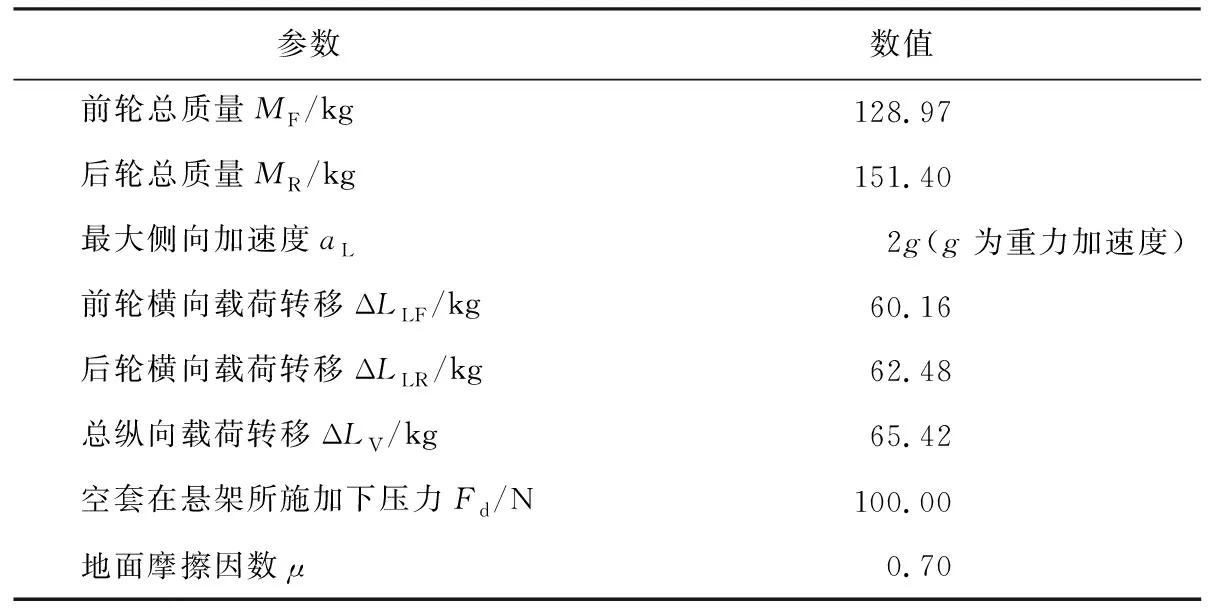
表1 参数信息Table 1 Parameter information

2.1.1 上、下销点受力计算

悬架受力如图3所示.图中:FL为外侧车轮侧向力;FV为地面垂直力;F1为上销点受力;F3为下销点受力沿下横臂方向分力;F4为上销点受力指向下销点方向分力;F5为推杆受力;α=1.98°;β=1.18°;γ=86°;δ=56.65°.

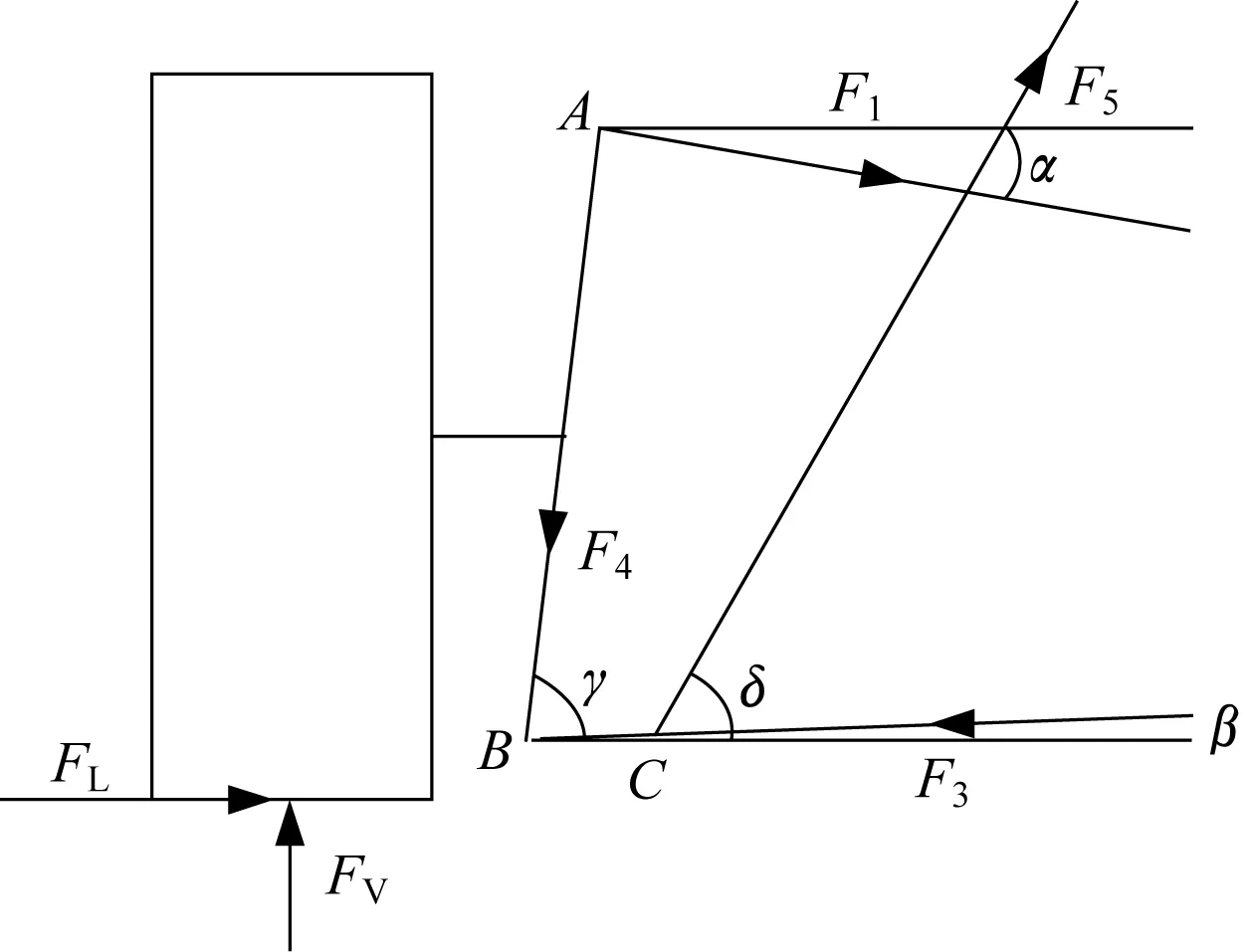
图3 悬架受力示意图Fig.3 Schematic diagram of suspension force

利用力平衡公式,分别计算出F1、F3、F4的值和下销点在YZ平面内受力.为计算上、下销点在X方向受力Fa与Fb,需先计算制动力FB,在A点和B点利用力平衡公式[3]计算Fa、Fb,如图4所示.其中:FB=μFV;轮胎半径R=228.6 mm;O点与A点直线距离OA=90.7 mm;O点与B点直线距离OB=81.92 mm.

2.1.2 上横臂受力计算

由销点受力F1、F3可以算出上横臂受力F11、F12与下横臂受力F31、F32,如图5所示.其中:φ1=19.22°;φ2=20.52°;φ3=22.12°;φ4=23.84°.

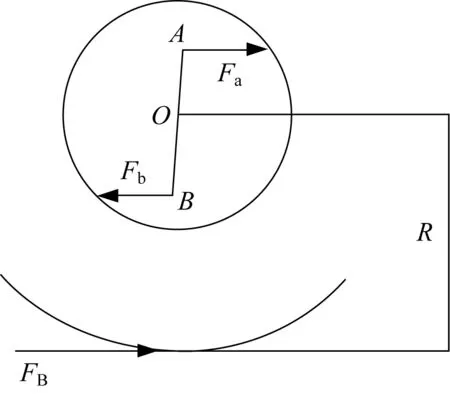
图4 轮边纵向受力示意图Fig.4 Schematic diagram of longitudinal force on wheel edges

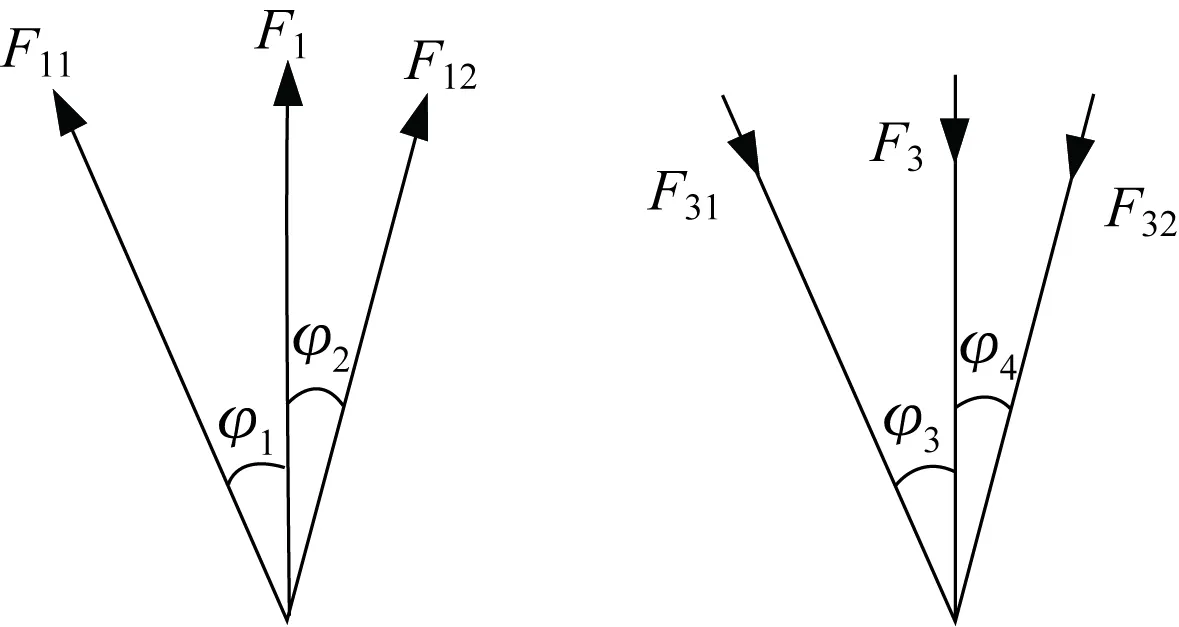
图5 上横臂受力示意图Fig.5 Schematic diagram of force on upper transverse arm

2.1.3 下横臂推杆受力计算

计算销点受力F1、F3、F4的值,在B点和X、Y轴方向,利用力平衡可得出推杆受力F5以及下横臂与车架铰接点等效合力水平分力FDX和竖直分力FDY,如图6所示.

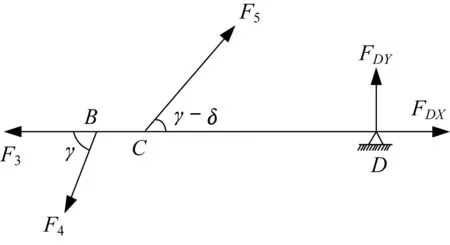
图6 下横臂受力示意图Fig.6 Schematic diagram of force on lower transverse arm

2.1.4 摇臂固定吊耳受力计算

本文摇臂与推杆之间传递比为1,推杆与摇臂连接点F受力等于推杆受力F5,E点处摇臂固定吊耳可以看作一个固定铰支座,摇臂受力如图7所示.在X、Y轴方向和F点,利用力平衡公式得出F6、FEX、FXY.其中:θ=10.41°;E、F点水平距离为28 mm;E、F点竖直距离为19 mm;F、G点水平距离为28.24 mm;F、G点竖直距离为26 mm.

图7 摇臂受力示意图Fig.7 Schematic force diagram of rocker arm force

2.1.5 车架吊耳受力计算

上横臂可看作二力杆,故与上横臂相铰接车架吊耳受力与上横臂受力大小相等,方向相反.下横臂由于推杆作用不可直接简化为二力杆计算,应依据下横臂与车架铰接点等效合力计算,方法与计算上横臂受力类似.减震器吊耳受力与F6大小相等,方向相反.

2.2 制动工况

制动工况分析模拟赛车75 m直线加速(赛道从起点到终点直线距离[1]为75 m)后迅速制动情况.赛车在加速结束后需要立即制动,此制动阶段产生的制动减速度为最大值,计算此时悬架硬点处集中载荷.由于车架设计左右对称,车架两侧对称硬点受力大小一致,方向不同.按车架载荷处理过程[4-7]计算车架一侧硬点集中载荷.

制动时前悬架地面垂直力为

(1)

制动时后悬架地面垂直力为

(2)

制动时外侧车轮侧向力为

FL=0

(3)

依次处理制动时车架吊耳受力,计算结果分解为X、Y、Z轴上分力,见表2.

表2 制动工况悬架硬点载荷Table 2 Suspension hard point load under braking condition N

通过对制动工况下车架载荷施加及约束得到车架应力和应变云图,如图8和图9所示.

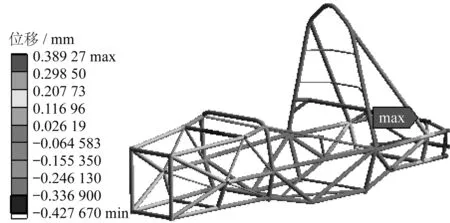
图8 制动工况挠度云图Fig.8 Deflection cloud diagram of braking condition

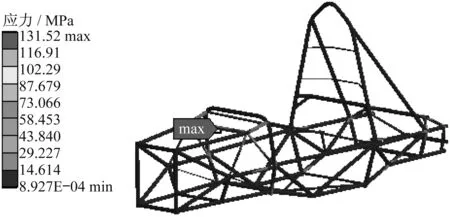
图9 制动工况应力云图Fig.9 Stress cloud diagram of braking condition

车架最大应变0.389 27 mm,位于后悬架减震器安装杆中部.车架最大应力131.520 MPa,位于前悬架减震器安装硬点处,小于30CrMo合金钢屈服极限强度785 MPa[8-9].故该工况满足要求.

2.3 加速工况

加速工况模拟赛车75 m直线加速时最大加速度受力情况,赛车手通过不断换挡改变赛车行驶速度.由于车架设计左右对称,两侧对称硬点受力大小一样,方向不同,因此计算车架一侧硬点集中载荷[4-7]即可.

加速时前悬架地面垂直力为

(4)

加速时后悬架地面垂直力为

(5)

加速时外侧车轮侧向力为

FL=0

(6)

依次处理加速时车架吊耳受力,计算结果分解为X、Y、Z轴上分力,见表3.通过载荷施加及约束得到车架应力和应变云图,如图10和图11所示.

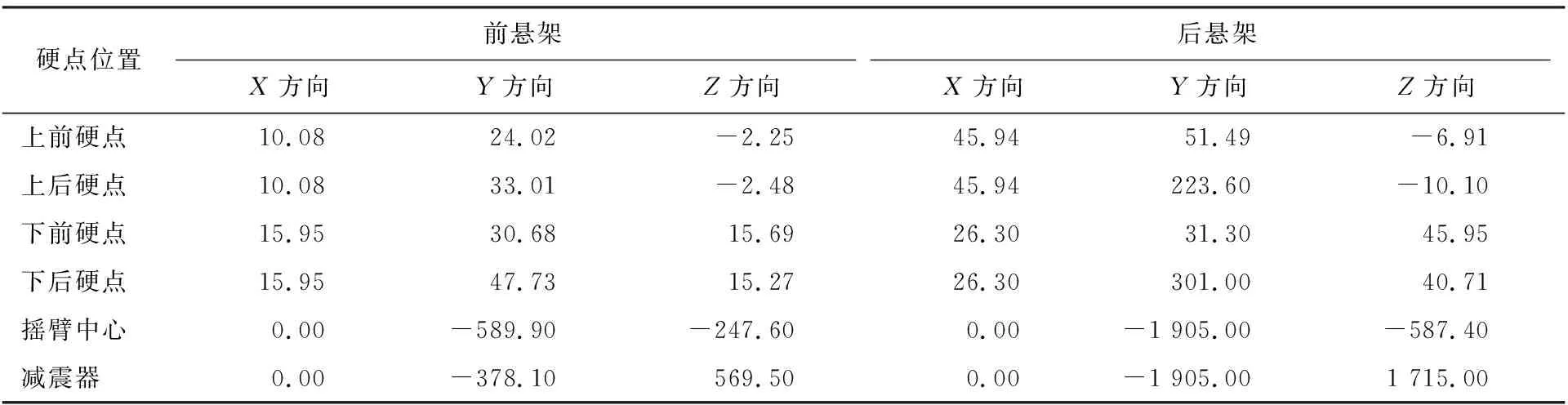
表3 加速工况悬架硬点载荷Table 3 Front suspension hard point load under acceleration condition N

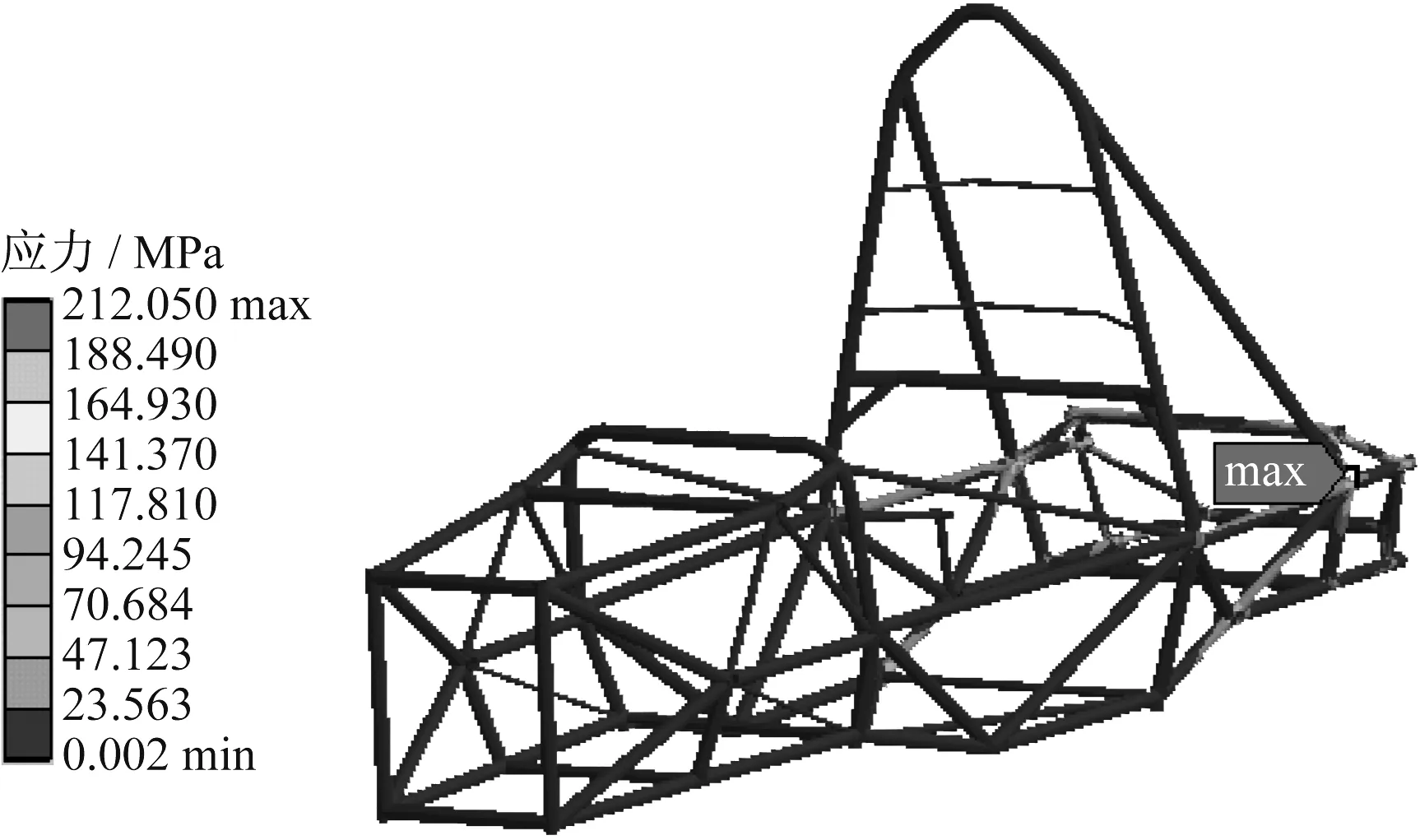
图10 加速工况应力云图Fig.10 Stress cloud diagram under acceleration condition

车架最大挠度1.092 50 mm,位于后悬架减震器安装杆中部.车架最大应力212.050 MPa,位于后悬架减震器安装杆支撑节点处,小于30CrMo合金钢屈服极限强度[8-9].故该工况能满足设计要求.

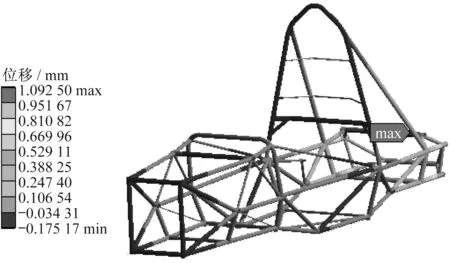
图11 加速工况挠度云图Fig.11 Deflection cloud diagram of acceleration conditions

2.4 转弯工况

转弯工况模拟赛车进行8字环绕项目[1](两个同心圆成8字形排列,两个圆心之间距离为18.25 m,内圆直径15.25 m,外圆直径21.25 m).由于转弯时对称硬点受载荷不均匀,需分别计算车架两侧硬点集中载荷,计算转向时内、外侧受力[4-7].

前悬架转向内侧轮垂直力为

(7)

前悬架转向内侧轮侧向力为

(8)

后悬架转向内侧轮垂直力为

(9)

后悬架转向内侧轮侧向力为

(10)

前悬架转向外侧轮垂直力为

(11)

前悬架转向外侧轮侧向力为

(12)

后悬架转向外侧轮垂直力为

(13)

后悬架转向外侧轮侧向力为

(14)

依次计算前悬架和后悬架吊耳受力,计算结果分解为X、Y、Z轴上分力,见表4和5.车架应力和应变云图如图12和13所示.

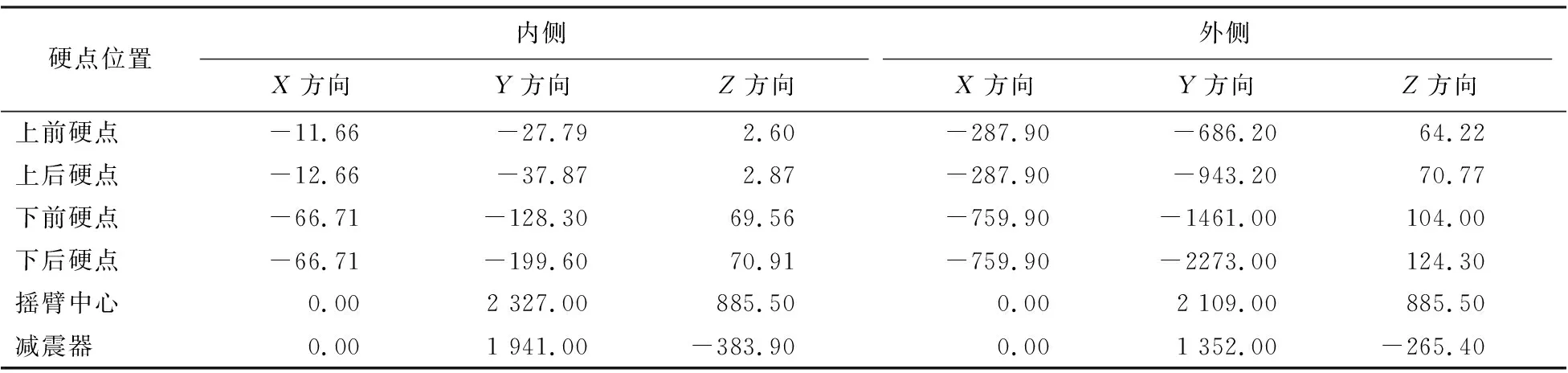
表4 转弯工况前悬架硬点载荷Table 4 Hard point load of front suspension under turning condition N

表5 转弯工况后悬架硬点载荷Table 5 Hard point load of rear suspension under turning condition N

图12和图13表明车架最大挠度6.454 2 mm,位于举升杆处.车架最大应力480.66 MPa,位于车架主环最低点处,小于30CrMo合金钢屈服极限强度.故该工况满足设计要求.

2.5 自由振动

模态是结构系统固有振动特性,通过对模态分析预先避免车架与发动机和地面共振.车架受到外部激励主要包括赛道颠簸和发动机气缸爆发与活塞运动产生振动.本文发动机选用CBR600,通过对CBR600发动机标定,常用转速为7 000～9 000 r/min.发动机产生激励频率与转速和气缸数关系[10]为

(15)

图12 转弯工况应力云图Fig.12 Stress cloud diagram of turning condition

图13 转弯工况挠度云图Fig.13 Deflection cloud chart of turning condition

式中:f为发动机激励频率;n为发动机转速;z为发动机缸数;i为发动机冲程数.

CBR600发动机为4缸4冲程发动机,其常用转速激励频率为233.3～300 Hz.车架振动频率要求避开发动机激励频率,减少车架因发动机运转而产生共振现象.车架自由振动属于无阻尼多自由度问题,可利用n自由度无阻尼自由振动[10-11]方程求解得到,方程为

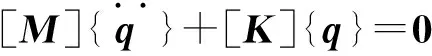
(16)

通过Workbench软件Modal求解器对其前12阶求解,车架自由模态分析没有外部载荷和约束,因前6阶频率较小,为刚性模态,剔除前6阶频率.7～12阶结构模态如图14所示,模态频率见表6.

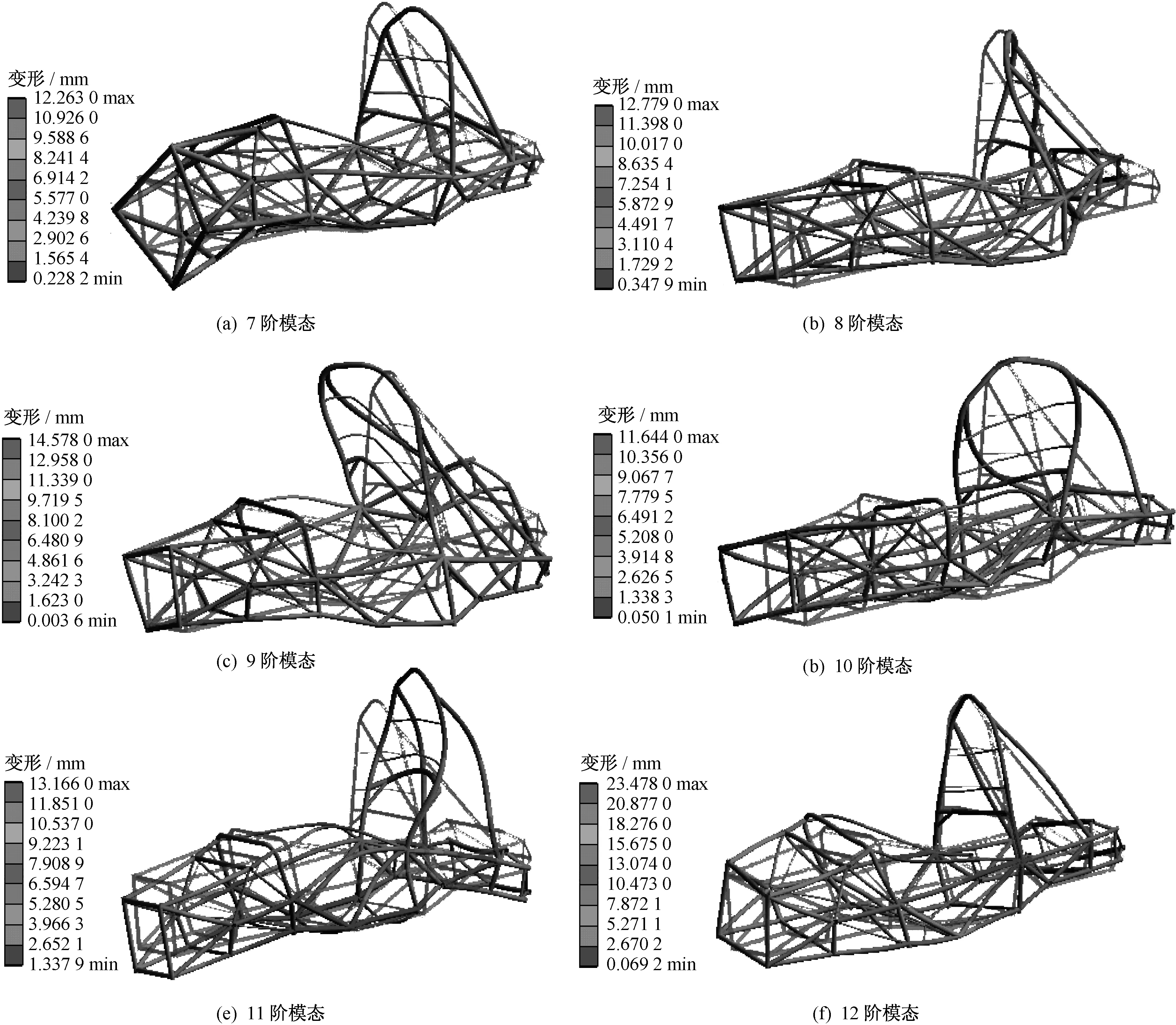
图14 车架模态振型图Fig.14 Mode diagram of frame

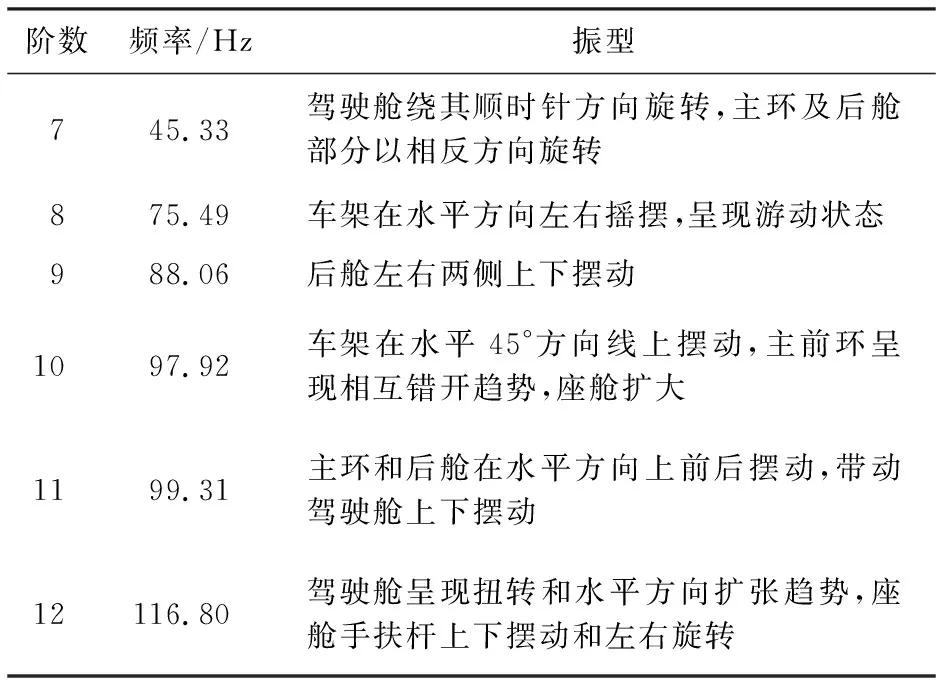
表6 车架模态频率Table 6 Modal frequency of frame

车架结构模态在X轴、Y轴和Z轴上发生不同程度变形,车架最低振动频率45.332 Hz,最大振幅23.478 mm,小于25 mm[1].由于赛道地面振动频率在1～20 Hz,而车架结构模态最低频率高于地面振动频率,车架不易和地面发生共振[10-12].模态分析中,车架最高振动频率116.77 Hz,由式(15)计算发动机重新标定后常用转速振动频率为233.3～300 Hz.发动机工作时常用转速最低频率远高于车架最高振动频率,车架在结构设计上不会与发动机发生共振.

3 结 论

1) 通过计算极限工况下悬架系统各个硬点处集中载荷,得出赛车转弯时单侧车架硬点受到集中载荷值较大,分解为X轴、Y轴和Z轴受力后可较为准确得出车架载荷大小.

2) 通过车架制动、转弯和加速工况下集中载荷仿真分析,得出车架在转弯工况下变形最大,其最大挠度6.454 2 mm,位于车架尾部,最大应力480.66 MPa,满足30CrMo合金钢材料属性要求.

3) 通过车架自由振动分析,可知其结构模态频率分别为45.33、75.49、88.06、97.92、99.31和116.8 Hz,满足模态要求,能最大程度减少与发动机共振.