在深度教学中引发学生的数学思考
王霞飞


子曰:“学而不思则罔,思而不学则殆.”这说明学习思考的重要性.《义务教育数学课程标准(2011年版)》在课程目标的总体目标中明确指出“通过义务教育阶段的数学学习,学生能够初步学会运用数学的思维方式去观察、分析现实社会,去解决日常生活中和其他学科学习中的问题,增强应用数学的意识”,并把“数学思考”作为小学生数学学习的四大目标之一.可见,培养小学生的数学思考能力单靠教师浅层次的课堂教学是无法实现的,只有教师深度地教,学生深度地学,不断地提高课堂教学的品质、丰富课堂教学思维的内涵、创建有效的课堂教学活动,才有可能引发学生学习数学的思考能力.
如何在深度教学中引发学生的数学思考呢?我认为可以聚焦以下几个方面.
一、关注学生的认知起点,学会思考
美国教育心理学家奥苏伯尔在《教育心理学》一书的扉页中指出:“如果我们不得不将教育心理学还原为一条原理的话,我将会说,影响学习的最重要因素是学生已经知道了什么,我们应当根据学生原有的知识状况进行教学.”因此,数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上.那么,在教学实践中,教师该如何把握学生的学习起点呢?
例如,教学“除数是整十数口算除法”,课件出示教材生活情境图,通过学生观察、思考得出口算“80÷20”这一算式,学生会怎么样算出结果呢?这时教师引导学生通过小组合作,借助已有的认知,归纳得出不同的口算方法.
1.动手操作法:这时最原始的方法.
10根小棒一捆,80根小棒8捆,再两捆放一堆,可以放四堆,所以80里面有4个20,80除以20就得4.
2.乘法逆推法:算除法、想乘法.
4个20是80,80除以20得4.
3.合并计数法:把80想成8个十,把20想成2个十,8个十除以2个十得4.
4.迁移类推法:因为8÷2=4,所以80÷20=4.
通过借助学生原有的生活和学习经验,总结出了“除数是整十数口算方法”,可以用动手操作法、逆推法、迁移类推法和合并计算法,得出80除以20的结果.同时,学生在独立应用竖式验算80÷20时,商4都写在了个位上,并会总结出笔算两位数除以整十数的计算方法.深度教学提倡用各种方式了解学生已有的知识经验,再根据这些“前经验”对所学知识进行加工,寻找学生学会、会学、易学的有效途径,让学生学会自己思考数学问题.
二、深入挖掘教学知识,拓展思考
《教材》是教师进行教学的依据,是教师用来教学的材料,也是学生用来学习的材料.教师使用教材需要教育的智慧.在新课程改革中,教师不是教教材,而是要用教材教.这不仅是一个教学理念的转变问题,而且是一个教学实践的操作行动问题.在教学实践中,教师要深入挖掘教材编写的真正意图,它的变化以及发展趋势.宏观上,整体把握现行教材各个版本,理清所使用教材的编排特点与编排体系.微观上,对教材所涉及的知识点、各领域知识结构的内在和分布情况进行细致的研究,达到触类旁通.只有将教材了然于胸,才能确定好教学的重点与难点,找准教学的切入点,发展学生思维.决不能照葫芦画瓢,以至于误人子弟.
例如,学习了两位数乘两位数笔算乘法之后,像65×54=3 510,这道题的结果正确吗?许多学生会想到进行验算,并呈现以下方法:
84×65=5 460 5 460÷65=84 5 460÷84=65
一般情况下教师讲到这里就止步了.这时笔者追问学生除了上面方法之外,还要别的验算方法吗?看谁见多识广!一石激起千层浪,一名学生说:“老师,我看过课外书,可以推荐一种更好的方法给同学参考.”笔者抓住时机让他上台展示,他有条有理地展示了自己的想法.
1.在黑板上画一个大叉.
2.把一个因数乘数各位上的数字加起来,如果得到的数是两位数,再把这两个数字加起来.如上面被乘数是84,8+4=12,1+2=3,然后把3写在右边,如3.
3.把另一个因数也按照上面的方法加起来,6+5=11,1+1=2,把2写在左边,如23.
4.把积5460也按照上面说的方法加起来,5+4+6+0=15,1+5=6,写在的上边,如23.
5.再把23左右两边的数字相乘写在23,如果左右两边相乘是两位数,也要按照上面说的方法加起来,写在下边.
经过以上思考,得出上下数字相同,就表明结果是正确的,否则就是错误的.
学生接着用这种方法验算下面题584×275=160 600,发现这种方法很好,容易接受、理解.
在深度教学中,教师重视启发学生挖掘教材资源的潜力,凝聚优质教学资源,注重挖掘教材的深度,拓展学生的数学思考,有利于培养学生的数学思考能力.
三、力求知识结构化,优化思考
知识系统化是把零碎的知识形成知识网络结构,包含两层意思学习内容系统化和学习方式系统化.深度学习要力求让知识学习和能力的培养达到结构化,让学生学得轻松,学得系统.
如何让知识的学习结构化?教学中教师要设计一些有趣的数学活动,简化一些繁杂的教学流程,让教学结构简单化,并给予学生足够时间和空间,围绕优化学生思考方法去展开教学.
比如,在“鸡兔同笼”教学中,教师紧紧抓住数量关系这个核心,让学生根据教材展开教学,一步一步优化思考方法.
为了研究方便,依据教材把原题的数字改小一点:笼子里有若干只鸡和兔,从上面数,有8个头;从下面数,有26条腿.鸡和兔各有几只?
先让学生理解关在笼子里鸡和兔给我们带来的数学信息:① 鸡和兔共8只;② 鸡和兔共有26条腿;③ 鸡有2条腿;④ 兔有4条腿.
在理解题意,获得信息之后,学生进行解答.
1.猜一猜,尝试探究
生1:有3只兔,5只鸡,可是算出来的腿是4×3+2×5=22(条),比实际的要少.
生2:如果有4只兔,4只鸡,算出来的腿是4×4+2×4=24(条),比实际的还是少了.
师:很不错!算得很有道理.但我们发现,盲目、凌乱猜不容易找到正确的答案.
生3:那我们按照顺序列表吧!
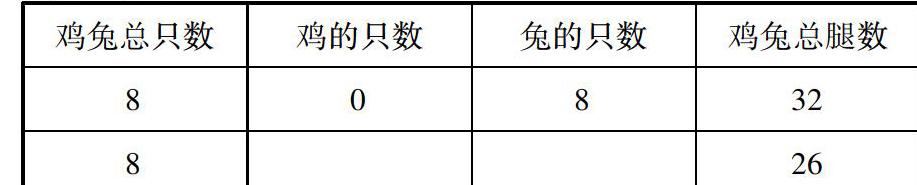
2.按照顺序列表解答.
师:请同学们仔细观察表格,想一想你有什么发现?
生4:每减少1只鸡,增加1只兔,腿就增加2条.
生5:像刚才猜测时22条腿,我们只要把鸡换成兔,因为比实际少了26-22=4(条)腿,只要把2只鸡换成2只兔就可以了,因为1只鸡比1只兔少2条腿,这样鸡就是3只,兔就是5只.
生6:哦,明白了,每把1只兔换成1只鸡,总腿数就增加2条;换2只兔增加4条.换3只增加6条,换4只增加8条……
师:那我假设全是兔呢,就应该有32条腿,与实际26条腿相比,多出32-26=6(条),那我应该增加鸡还是兔呢?增加几只?
生7:因該增加鸡,增加6÷2=3(只).
师:要是全是鸡呢,总腿数是16条,比实际少了26-16=10(条),需要怎么调整?需要调整几次?
生8:需要增加兔,调整10÷2=5(次),也就是增加5只兔.
在猜测的基础上,引导学生思考这种方法不恰当.再在猜测的基础上,让学生一一列表,从无序思考到有序思考,发现其中隐藏的规律,发现规律的变化,学生对规律有了一定的感性认识,再引导学生上升到抽象的假设法,学生在理解假设法同时也沟通了各种方法之间的内在联系,一步一步将知识结构化,帮助学生积累活动经验,把握解题策略,优化思考方法.
总之,用深度教学的行动去引发学生学习数学思考,需要教师从学生的已有的经验出发,尊重学生的认知规律;需要教师对学生的学习方式进一步探究,深入挖掘教学知识,拓展学生的思路;更重要的是还需要教师对知识结构的深入思考,引导学生用数学的眼光去观察、分析、解决现实生活中的问题,构建有儿童味的数学课堂体系.只有这样,才能让深度教学真正引发学生的思考,体现数学教学的价值.

