变式教学 变出精彩

肖宇鹏

摘 要：在初一阶段的学生已经学过一元一次方程的应用，根据实际题干条件来设出未知数，列出一元一次方程求解来解答问题，但有的实际问题所列出的方程不是一元一次方程，而是一元二次方程，这就是本节课所要研究的一元二次方程的应用——关于面积和体积方面的实际问题。班级学生整体学习氛围较为浓厚，有着良好的学习习惯。

关键词：变式教学;初中数学;一元二次方程

在本节课中，学生要经历和体会以一元二次方程来解答生活中的问题，认识到一元二次方程的重要性，发展自身逻辑思维能力、分析和解决问题的能力。

一、 复习巩固，引入话题

在前期的学习中，学生已经学过为一元二次方程铺垫的知识，教师不妨引导他们先进行复习，再自然引入本节课话题，避免教学内容的突兀，使班级学生自然过渡到本节课之中。

师：我们已经学习了与一元二次方程相关知识（概念、定理和运算法则等），大家思考下它与一元一次方程之间有着怎样的区别和联系？

生：二者间都有一个未知数，一元一次方程未知数最高次数为1次，另外一个为2次，一元一次方程解只有1个，另外一个有2个解。

师：概念不同，解法不一样，解的情况也有所不同，这就说明一元二次方程的解法较为复杂，在选择解法过程中要注意方法。那么，它们之间又存在着怎样的联系呢？

生：一元二次方程均可以化为一元一次方程。

师：我们学习新知识要基于旧知识，那么，一元二次方程实际问题解题步骤是什么？

生：审题、根据题干材料来设未知数、列出等式方程、运用所学知识解方程、最后验证答案是否符合要求。

师：其中，最关键的步骤是什么？

生：根据题干信息来寻找等量关系。

师：认真审题非常重要，那么，我们今天就来研究如何利用一元二次方程求解与面积和体积相关的问题。

【设计意图】：知识复习和引入简单明了，从一元一次方程以类比学习方法来总结得到一元二次方程解决问题的步骤，引导学生进入本节课学习主题。

二、 问题探究，变式训练

问题一：一根长度为22cm的铁丝。（1）假设王叔叔要把铁丝做成一个面积为30cm2矩形，求取矩形的长与宽。（2）如果要把矩形面积设计为32cm2，是否可以完成上述要求？

教师引导学生分析题干信息中的已知量和未知量，找到已知量为矩形的面积和周长，未知量为矩形边的长度。

学生阅读题干信息，找到已知量和未知量，设矩形的边长为xcm，另外一边长为（11-x）cm，找到其中的相等关系，在练习本上列出方程，判定解是否存在。针对班级学生可能出现的问题，教师在练习时到台下巡视、指导，师生共同完成试题。在完成问题基础上，教师再布置一些变式试题，既能巩固所学知识，又能发散数学思维。

变式问题一：要想建立一个面积为20cm2的长方形场地，如果一边靠着长6m的墙，其余三条边用长度为13m的围栏围成，那么，这个围成的长方形场地边分别为多少？

（学生独立完成后，教師选择具有小组代表到讲台进行讲解。）

组1：假设长方形的宽度为xm，那么长度为（13-2x）m。

组2：假设与墙平行四边形的长度为xm，那么它的宽度为13-x2m。

变式问题二：如图2，假设其他条件不变，要在长方形长边上开出一道1m的门，那么，围成的长方形场地长和宽各位多少？

（学生独立完成后，教师选择具有代表性的小组代表进行回答。）

组1：设长方形的宽度为xm，那么长度为（13+1-2x）m，长方形面积为x（13+1-2x）=20。

组2：设长方形的宽度为xm，那么长度为（14-2x）m，长方形面积为x（14-2x）=20。

组3：设长方形的长度为xm，那么宽度为14-x2m，长方形面积为x14-x2=20。

归纳环节：

师：在解决问题过程中，大家回忆一元一次方程的解法，探讨如何来类比应用，在学习中有何收获。

生1：要认真阅读题干信息，找到隐藏在其中的等量关系。

生2：一元二次方程的求解要比一元一次方程复杂，解出答案后要对解进行验证，看是否符合题干要求。

生3：本题是与面积相关的试题，假设未知量时要与长度和宽度有关。

生4：对未知量进行假设是本道试题解题的关键所在。

总结：阅读题干—找到等量关系→做出假设—设未知量→进行求解—选择恰当解法→注重检验→关注题干条件。

【设计意图】：精心设计关于铁丝围长方形试题，以变式教学来注重培养学生数学方程思维，使他们能够灵活应用思维来学习，在课堂中引导其进行数学思考，帮助个体掌握解决的方法。在试题练习的过程中，教师在教室中来回巡视，强调解答一元二次方程的注意事项，指导解题方法，使学生认识到一元二次方程重要性，借助一元一次方程的解法来提升他们的类比迁移能力，拓展其数学思维，达到高效率的课堂教学效果。

问题二：某块长方形铁皮，长度是宽度的两倍，四个角各自截掉一块正方形，制作出高度为5cm、容积为500cm3的无盖长方体容器，那么，求这块铁皮的长度和宽度。出示试题后，学生用教具来演示长方体折叠过程。

学生对照教具，找到题干材料中隐藏的等量关系。

生1：长方体体积为500cm3，即，长乘宽乘高。

生2：长方形铁皮长度是宽度的两倍。

生3：设铁皮的宽度为xcm，那么长度为2xcm，列出方程：5（x-10）（2x-10）=500。

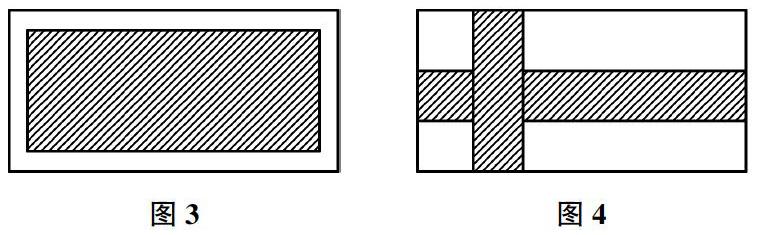
变式问题一：（1）如图3所示，长方形草坪长度为30，宽度为15，在草坪的四周是等宽的路，如果包含路在内的长方形面积为544，那么，道路宽度为多少。

（2）已知包含等宽路在内的长方形草坪长度为30，宽度为15，其中，草坪的面积为364，那么，道路宽度为多少。

生1：假设道路宽度为x，根据题干信息得：（30+2x）（20+2x）=544。

生2：假设道路宽度为x，根据题干信息得：（30-2x）（20-2x）=544。

师：那么，根据上述知识，我们在生活中是否能得到以上述方程为模型的实际问题吗？班级学生积极回应，踊跃回答问题。

生1：家里装照片的相框。

生2：屋里的窗户中间是玻璃，外面有等宽的密封条。

生3：桌面上的桌布。

师：大家回答非常棒，可否根据上述方程来编写一道数学考题呢？

生4：为了让讲台变得更美，我们用班费买了一块讲台桌布，桌布的一边和讲台等齐，另外三边垂下等宽的宽度，求这个宽度为多少。班级学生纷纷根据题意来假设方程，列出方程式。

变式问题二：如图4所示，在长度为40m、宽度为22m的矩形地面内，有两条宽度相同且垂直的路，路之外铺设草坪，要使草坪面积达到760m2，那么路的宽度为多少？学生根据题目来独立完成，列出方程式。

师生共同总结用一元二次方程在解决面积和体积问题时的步骤、注意点，学会应用知识来解决与之相关的问题，从中体会到类比、转化的数学思想。

【设计意图】：根据长方形基本图形进行改变，设计出其他图形来进行变式教学，根据教学设计来与学生实际学情紧密结合，激发他们求知欲望，引导其把数学知识进行一般化思考，拓宽数学思维。小组合作引发个体对一元二次方程知识兴趣，活跃课堂氛围，引导学生当堂设计问题、当堂解答，加强对数学知识的理解和掌握，提升课堂学习质量和效率。

三、 教学反思

（一）明确变式目的

变式教学目的在于让学生在问题的变化中找到内在的本质，发散数学思维，从“不变”的规律中来探索规律，从而更加透彻的理解问题背后的本质，学会用“不变”的知识来应对“变化”的题目。在问题发展的过程中，教师要帮助学生在理解基础上来掌握如何解决问题，然后运用方法来解决数学问题，注重他们知识迁移能力的培养，拓宽个体的数学思维。

就本节课而言，教师展开变式教学目的在于运用一元二次方程来解决关于面积、容积的问题，在设计变式过程中通过改变题干信息、变换问题情境来创造出多种类型的变式，为学生练习创造更多机会，使他们从多个角度和层次对一元二次方程模型有更加深入理解，發散其数学思维，加强思维的变态。

（二）注重知识的生成

在实践教学中，教师往往注重例题自身的变式，忽视了知识形成过程中的变式，课堂教学效果不够理想。针对这一问题，教师不妨基于知识形成过程来思考如何对某个基本问题进行变式设计，引导班级学生运用数学思维来进行探究，使他们经历知识的生成过程，体会到一元二次方程的数学本质。

本节课授课的重点是一元二次方程解决面积和体积问题，如果不精心设计数学问题，课堂训练很容易变得机械、枯燥，试题讲解也只注重重复性训练。于是，从基本图形入手设计具有一定梯度的变式试题，把问题变成“问题串”，层层递进来推进数学课堂教学。

（三）提升课堂参与度

课堂教学效果在很大程度上取决于班级学生的课堂参与热情，没有了积极参与，哪怕再热情，教学效率也会大打折扣。精心设计的变式能够营造出一种宽松的课堂氛围，使每个人都能掌握最基本的数学知识，培养他们的应变能力，开拓学习思路。数学教师设计问题来激发班级学生学习好奇心，使他们产生浓厚求知欲，提升课堂参与程度。在设计问题时，入口问题相对较为简单，更容易被接受，借助于梯度问题来循序渐进展开教学，拓展数学思维，培养个体知识迁移能力。就本节课教学而言，设计的问题层层递进且贴近学生生活，还让他们现场编写试题、现场解答，取得了良好数学课堂教学效果。

总之，教师在教学实践中要注重变式的授课，依据教材和班级实际学情来合理安排讲课内容，因材施教开展数学教学活动，为班级学生设计出一节精彩的变式课，有效提升个体数学学习兴趣，使每个人都能乐在其中。

参考文献：

[1]陈焕琼.初中数学变式教学的过程性思考及案例研究[J].数学教学通讯，2017（12）.

[2]金荣.初中数学变式教学应用研究：以“探索勾股定理”的教学为例[D].呼和浩特：内蒙古师范大学，2017（11）.

[3]杨昌兰.基于素养立意的初中数学课堂教学设计：以“垂直于弦的直径”为例[J].中学数学教学参考，2017（10）.

[4]陈峰.“一题多解”是提高初中数学教学有效性的“催化剂”[J].中学数学研究：华南师范大学版，2017（9）.