基于非支配排序遗传算法并联仿生眼构型优化设计

陈志 阳复建

1 桂林航天工业学院 机械工程学院，广西 桂林 541004；2 桂林航天工业学院 科技处 ，广西 桂林 541004

低空空域的监视往往存在环境复杂、干扰多，监视范围广等问题，为了满足低空监视要求，视觉监控系统应当具备较大的视野以及较高的运行精度[1]。在机器视觉系统中所采用的摄像机主要是模仿脊椎动物的视觉构型，使摄像机获得大范围、高精度图像，从而满足低空监视的需求[2]。

目前，国内外学者致力于研究模仿人眼外肌功能的并联仿生眼机制。对于并联仿生眼配置设计，Ganesh等[3]开发了一种灵敏的三自由度(3-DOF)正交球面并联仿生眼机制；Daneshmand等[4]设计了一种改进的3-DOF并联仿生眼机制，允许眼动模拟器安装在人形机器人的头部；Wang等[5]提出了一种气动肌肉仿生眼机制，通过模拟6个眼外肌来实现相机的3自由度旋转。对于并联仿生眼造型的结构参数优化，Huo等[6]采用了一种分析方法，考虑所提出的全局灵活性指数，以实现最佳的全局准确性。Villgrattner[7]使用隐式过滤算法来优化结构参数，以最大工作空间体积比作为优化目标。从当前研究现状来看，针对大视场和高精度运动的并联仿生眼造型的研究较少，且在仿生眼造型参数优化方面大多采用单目标优化，而对于并联仿生眼造型而言其机构灵敏度、动平台倾角、运动精度以及运动传递性能均与造型的结构参数有关，因此采用单目标优化很难使结构参数同时取优[8]。

鉴于此，首先分析仿生眼原理，设计并联仿生眼造型的三自由度配置，并通过运动学分析求解运动性能指标。其次，采用改进的非支配排序遗传算法(NSGA-II)[9-10]来优化运动平台的运动性能，并根据优化的结构参数进行系统的动态模拟。最后建立实验平台，并将模拟结果与测量结果进行比较。

1 并联仿生眼造型的仿生原理和配置设计

1.1 人眼外肌的结构和功能

人眼外肌是附着在眼球上的肌肉，其主导着眼球的运动。每只眼睛有6个眼外肌。如图1所示显示了人类右眼眼外肌的解剖结构，6个眼外肌并联形成，根据拉动方向分为4个直肌和2个斜肌。其中，内直肌和外直肌构成一对水平肌，上直肌和下直肌构成一对垂直肌，而上斜肌和下斜肌构成一对斜肌。这3对肌肉可以驱动眼球围绕水平、垂直和视轴旋转，水平和垂直轴周围可达±38°，眼球运动精度约为0.02 °。此外，眼球运动的角速度可达400 °/s，角加速度可达500 °/s2。另外除了下斜肌外，6个眼外肌均来自后方常见的腱环，这使得眼外肌和眼球构成了一个并联机构。

图1 人眼外肌的解剖结构

1.2 设计目标和配置设计分析

为了给仿生眼提供至少180°的视野，根据本研究中使用的90 °视角相机，可以确定动平台应该在任何径向轴周围具有至少±45 °的倾角。此外，眼球运动精度应不超过0.05 °，从而实现连续平滑的追踪目标。另外，为了在仿生眼造型调整过程中提高搜索效率并保证图像清晰度，动平台的角速度应达到30 °/s，角加速度应达到500 °/s2。

所构建的仿生眼造型采用的是类似于人眼的眼外肌并联形式，需要保证平台至少能够在较宽的范围内绕2个径向垂直轴高速旋转。在动力驱动件上采用电动缸，该部件不仅可以提供推力，同时还可以提供拉力，而且在保证机构运动精度的基础上，通过自锁可以确保图像稳定性。除此之外，与普通的电动机相比，电动缸因线性运动的特点使得其具有良好的平稳特性以及较大的行程容积比。为了简化并联机构的结构且满足在2个径向垂直方向上高速旋转，采用3个电动缸的紧凑并联形式来模拟眼外肌的功能，实现动平台绕任意水平轴进行转动，保证运动精度应≤0.05 °，提供≥180 °的视野。另外，因为设计的是三自由度并联机构，该机构可实现平台沿O1X1和O1Y1轴旋转，并能够在O1Z1方向上径向移动，如图2所示。但是该机构在旋转过程中通常会伴随着摆动，将不利于目标的连续平滑跟踪。针对这一缺点，提出了如图2所示的“反Tricept”并联仿生眼配置，传统的Tricept机构由一个3自由度并联机构和一个2自由度串联机构经串接组成的混联机构。而“反Tricept”机构则是由一个2自由度并联机构和一个3自由度串联机构经过并联组成的混联机构。该配置主要由用于固定摄像机的动平台(A1A2A3)、定平台(B1B2B3)、主动链hiEi(i= 1,2,3)和从动链r组成。从动链被固定在定平台的等边三角形B1B2B3的中心O处，并且通过等边三角形A1A2A3的中心O1处的虎克铰连接到动平台。主动链由电动缸线性驱动，从动链为花键副，便于机构保持稳定。初始阶段时A1A2//B1B2和A2A3//B2B3，这使得动平台与定平台相互平行。图2中建立了基坐标系O-XYZ和副坐标系O1-X1Y1Z1，以O和O1为原点，OX和O1X1轴分别在OB1和O1A1方向，OY和O1Y1分别平行于B2B3和A2A3。通过这种构造方式可以对主动链的长度进行调整，从而使动平台能够绕O1X1和O1Y1轴旋转，即摄像机可通过合成两个方向的旋转来实现在任意水平轴方向上的快速转动，以获取较大的视野。

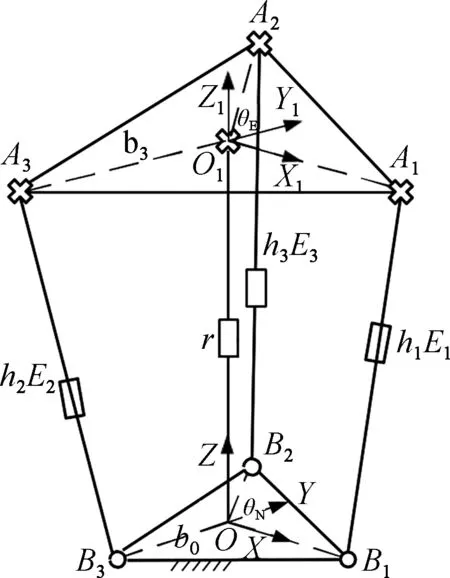
图2 并联仿生眼造型结构图

2 并联仿生眼运动学模型构建

尽管可以通过并联仿生眼配置保证摄像机围绕任何径向轴的旋转，但仿生眼造型的结构参数和性能指标(包括动平台的最大倾角和运动性能)尚未确定。为了获得满意的性能指标并选择合适的结构参数，构建了仿生眼运动学模型，并根据安装空间、铰链偏转、整体尺寸等约束条件对动平台的机构灵敏度、运动精度、平台倾角以及运动传递性能指标等进行多目标优化。

在闭链O-Bi-Ai-O1-O(i= 1,2,3)中，O-XYZ坐标系中O1的向量r=(xyz)T可由式(1)表示：

(1)

式(1)中，OBi表示Ai点在基坐标下的投影位矢；θN为仿生眼绕X轴的旋转角；b0为仿生眼基准点与眼部坐标系原点间的距离AiO1在O-XYZ坐标系下的投影；Ei、hi、分别表示AiBi的单位矢量和长度。

因为基坐标系O-XYZ为参考坐标系，因此R可由式(2)表示：

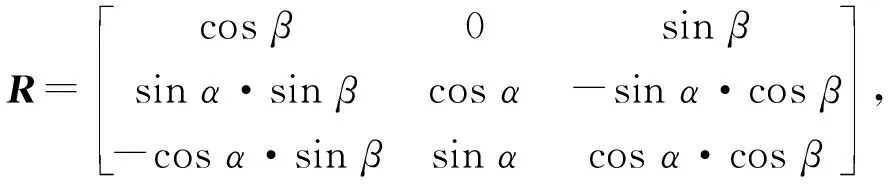
(2)

式(2)中，R表示标准旋转矩阵；α、β分别表示仿生眼相对基坐标系绕X、Y轴的旋转角，且α=θE+θN；θE表示仿生眼相对副坐标系O1-X1Y1Z1绕X1轴的旋转角，由此可以进一步得到：

(3)

式(3)中，b1为AiO1的长度，O1相对O-XYZ坐标系中的位矢r如式(4)所示：

r=hcEc，

(4)

式(4)中，hc表示O-XYZ中原点和O1-X1Y1Z1中原点间的距离；Ec=(cosαsinβ,-sinα,cosαcosβ)T为hc部分的单位方向矢量。根据仿生学原理可知，仿生眼结构对转动速度有着较高的要求，因此在模型构建中需要引入电机的角速度，并以此作为变量从而得到电机角速度与整体构型转动角速度之间的制约关系，如式(5)所示。

(5)

式(5)中，v表示仿生眼转动坐标系原点O1在OXY下的速度矢量。为了便于获取雅克比矩阵的最小条件数，将式(5)转换为：

(RO1A1)′=J1vm。

(6)

另外，将式(4)两边分别对时间进行求导，如式(7)所示：

v=J2vm。

(7)

令JD=J1+J2，为了将仿生眼、电机角速度引入到雅克比矩阵当中，进行如式(8)所示的变换。

(8)

此时J即为仿生眼造型的雅克比矩阵。

3 仿生眼造型优化

并联仿生眼造型的运动性能取决于动平台和定平台的初始距离以及半径等参数，为了使并联仿生眼造型获得良好的运动性能，需要对平台运转精度、最大倾角以及结构灵敏度等进行多目标优化。

根据参考文献[11]的分析，可以看出雅可比矩阵的平均条件数越小，运动学性能越好。此外，随着雅可比矩阵的平均条件数减少，仿生眼造型将变得“粗壮”，然而，随着动平台的最大倾角增加，造型将变得“细长”。因此，为了同时获得较大的倾角和良好的运动性能，采用多目标优化来进行权衡，其中将雅可比矩阵的最小平均条件数和动平台的最大倾角作为优化目标，如式(9)所示。

(9)

式(9)中，f1表示雅可比矩阵的平均条件数；f2表示动平台倾角相反数；θ表示动平台的倾角；σJmax、σJmin表示雅克比矩阵J的最大奇异值和最小奇异值。在结构设计中，仿生眼的运动主要受驱动件行程和安装空间的限制。此外机构的整体尺寸不应太大，以保证机构的良好动态性能。由于动平台在围绕OZ轴旋转过程中受到花键副的限制，因此在仿生眼造型运动过程中不会出现内部干扰现象。

进行多目标优化主要是为了确定动平台和定平台的半径以及二者之间的中心间距，因此提出决策变量如式(10)所示，其中b1为动平台半径，b0为定平台半径，hc为二者之间的中心间距：

X=[b1，b0，hc]。

(10)

目前，在多目标优化问题方面，国内外学者常将其加权到单目标问题中，这种研究方式虽然能够简化求解过程，但是对于不同目标的权重设定很难做到统一。采用改进的非支配排序遗传算(NSGA-II)对多目标问题进行优化，该算法的特点在于优化过程中不需要对参数进行调整且具有良好的寻优力。在多目标优化过程中，可通过拥挤距离来确定比较算子，从而获取多目标优化的最优前沿，最终确定并联仿生眼造型的结构参数。

4 结果和分析

4.1 优化结果验证

采用MATLAB实现多目标优化，为了选择合适的算法参数，在比较多组参数的优化结果后，最终种群个体选取为100，变异概率为0.12，交叉概率为0.905。为了保证算法能够搜索到最优前沿，在计算过程中从第10代开始，以10代为间隔，计算到110代。另外，为了增加结果的可信度，分别对每种进化代数进行10次最优计算，最后根据拥挤距离和前沿顺序选取最优的前100个非支配解。考虑到每次运算的结果均会出现一定的偏差，故针对不同进化代数所获得最终解，进行5次多项式拟合，如图3所示为进化代数为60次的拟合结果。

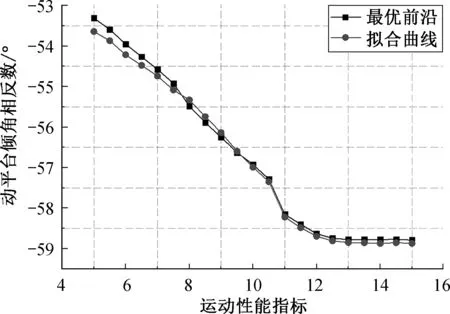
图3 60代最优前沿及拟合曲线对比图

为了获取最优前沿，以相邻2次迭代的最终解的拟合曲线方差小于一定值作为搜索到最优前沿的依据。如图4所示可以看出60代与100代的最优前沿接近重合，而50代未出现重合现象，从而可以进一步证明从60代起已经达到最优前沿。

图4 50代、60 代与100 代最优前沿对比图

针对复杂环境监视的实际需求，考虑到运动性能指标与平台最大倾角之间平衡确定并联仿生眼动平台的最大倾角为56.2 °，此时运动性能指标为7.31。优化后得到动和定平台的半径分别为38.1 mm和32.7 mm，两个平台之间的中心距离为154.4 mm。

4.2 动态模拟

并联仿生眼造型除了具有大视野和高运动精度外，还应具有良好的动态性能，能够快速搜索环境并快速跟踪目标。为了验证优化机制的动态性能，采用Pro / E来模拟系统的动态性能，模拟结果显示当动、定平台的半径分别为38 mm和32.5 mm，两个平台之间的中心距离为154.5 mm时获得最佳动态性能。在建模过程中考虑到所计算的最优参数以及模型构建的实际情况，对结构参数进行了优化，在模拟过程中，3个电动缸均以最大速度移动，模拟结果如图5和图6所示。从图中可以看出，动平台的倾角范围为-56.88 °～54.63 °，角速度可达106.1 °/ s，角加速度可达511.6 °/ s2。

图5 动平台角度模拟曲线

图6 角速度和角加速度模拟曲线

4.3 物理实验验证和分析

图7 实验模型

如图7所示为构建的实验模型。图8和9分别给出了当3个电动缸以最大速度移动时围绕O1Y1轴的动平台的角度曲线和角速度/角加速度曲线。图10为给定角度命令的并联仿生眼造型的运动控制曲线。陀螺测量结果表明，图8中动平台倾角范围为-56.48 °～54.47 °，图9中角速度可达99.23 °/ s，角加速度可达到502.5 °/ s2，在图10中，运动精度可以达到0.01 °，并且可以实现对运动目标的快速搜索和平滑跟踪，同时通过调整精度可以保证视频或图像的稳定性。

对比图8—10可以看出，测量的动平台的最大倾角(图8中的-56.48 °～54.47 °)略小于模拟值(图5中的-56.88 °～54.63 °)。出现这种情况可能是由加工和装配过程中的错误引起的，但是倾角仍然符合设计要求。此外，动平台的测量角速度和角加速度(图9中的99.23 °/ s和502.5 °/ s2)低于模拟结果(图6中的106.1 °/ s和511.6 °/ s2)可能是因为模拟过程中设定的初始条件与实际条件不同，系统内部存在的摩擦力无法准确模拟。然而，角速度和角加速度仍然可以满足设计要求。从图10可以看出，实际角度与期望角度重合，并联仿生眼造型的控制误差可以控制在0.01 °以内，满足设计要求。

图8 动平台角度曲线

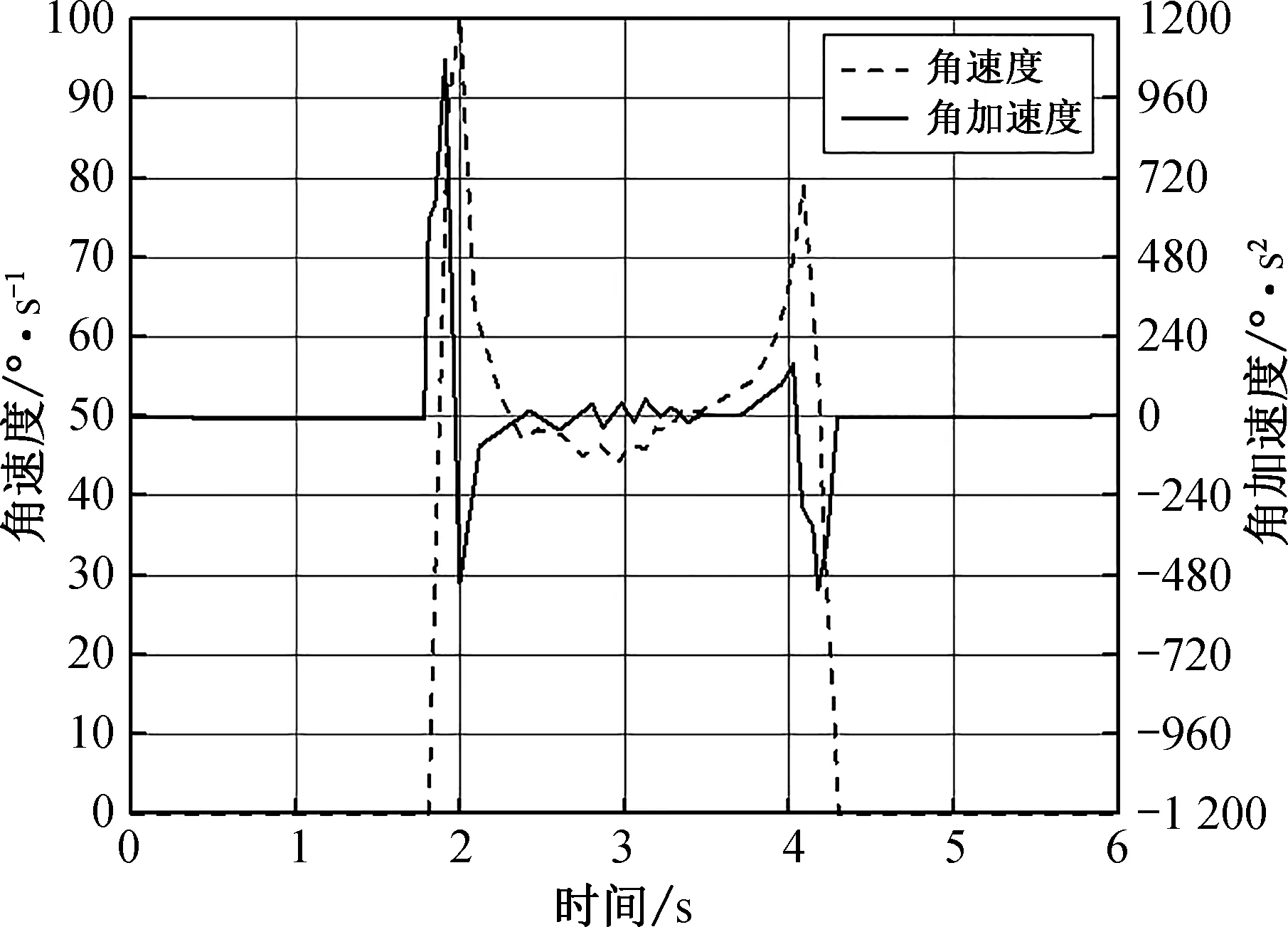
图9 角速度和角加速度曲线

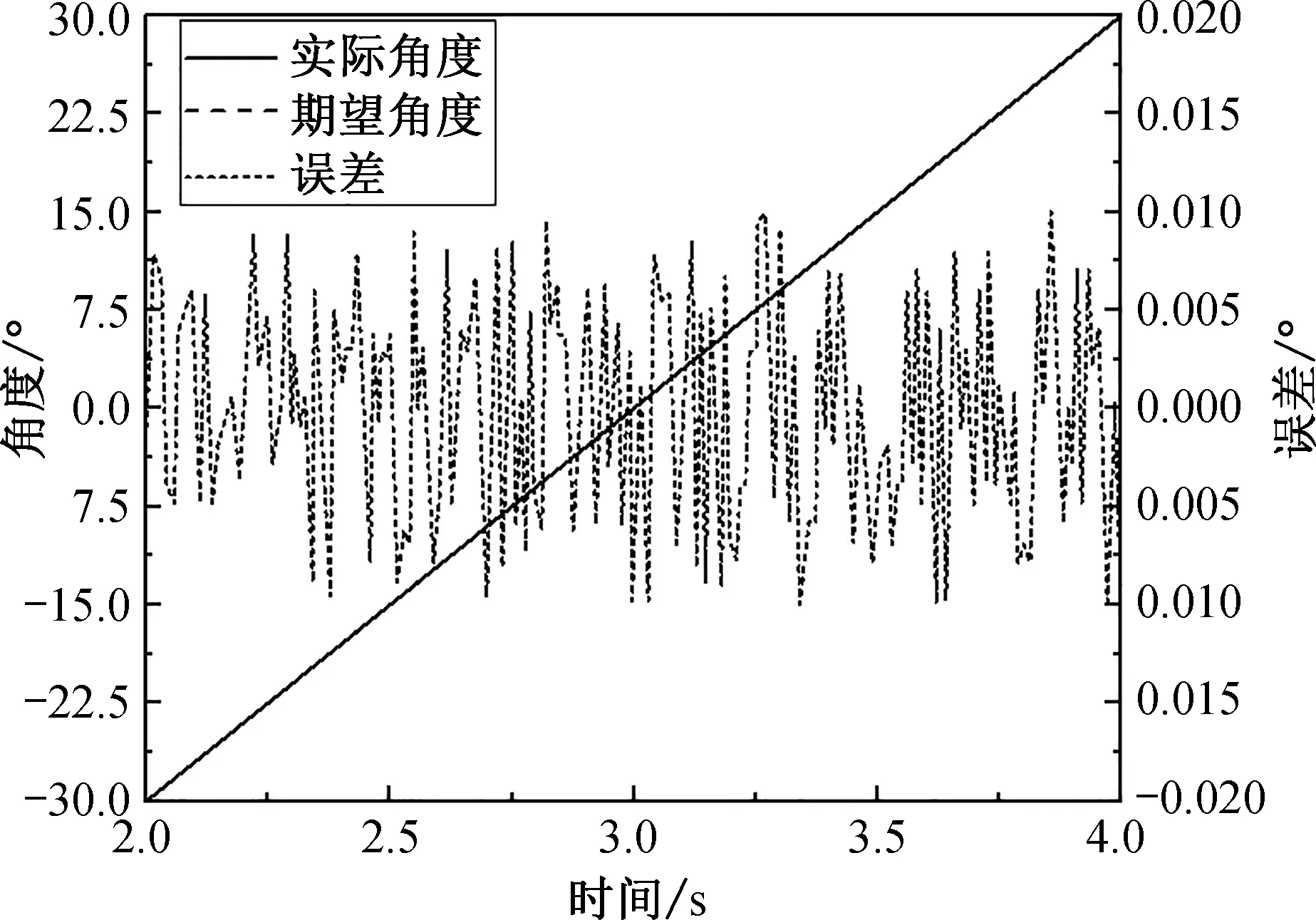
图10 仿生眼造型运动控制曲线

5 结论

通过模仿脊椎动物眼外肌的结构和功能，设计了一种新的三自由度并联仿生眼造型。利用NSGA-II算法对所设计的并联仿生眼造型进行运行精度、平台倾角、机构灵敏度以及运动传递性能等多目标优化，确定动、定平台的半径分别为38.1 mm和32.7 mm，两个平台之间的中心距离为154.4 mm。模拟和物理实验证明了设计的有效性，仿生眼具有0.01 °的眼球运动精度，99.23 °/ s的角速度和502.5 °/ s2的角加速度，可实现大视野搜索和快速、平滑的跟踪目标。