基于python语言的一种常微分方程神经网络解法
杨 震,陈豫眉,李 霜
(1.西华师范大学数学与信息学院,四川南充 637009;2.西华师范大学公共数学学院,四川南充 637009;3.西华师范大学计算方法及应用软件研究所,四川南充 637009)
0 引言
在科学计算及其工程应用中,常常需要求解微分方程.但解析方法只能用来求解某些特殊类型的方程,其他情况主要依靠数值解法.对于常微分方程问题,常用的差分方法有Euler方法,改进Euler方法和霍因(Heun)方法等[1,2].其中,Euler方法是一种最简单的单步法,计算量小,但精度低.改进的Euler方法由于增加了校正过程,在解的精度上有了较大的改进. Heun's方法是在Euler方法的基础上进一步改进,精度更高.近年来,神经网络在机器学习,深度学习,人工智能等各个领域取得了显著的发展,应用神经网络解决微分方程的问题已经成为热门.文献[3]中利用余弦基神经网络求解常微分方程.文献[4]中利用神经网络与小波分析求解微分方程.1988年,Lagaris和Likas提出了一种求解偏微分方程初边值问题的神经网络算法[5].由于单隐层神经网络可按任意精度去逼近任何的连续函数,所以该算法可以用于解决微分方程问题.2010年,Baymani,Kerayechia,EffatiS使用神经网络算法去求解stokes方程[6].2017年,Raissi,Perdikaris,Karniadakis提出基于高斯过程的神经网络算法[7].Long,Lu和Ma提出基于卷积微分算子求解偏微分方程的神经网络算法[8].2018年,Han,Jentzen等人提出了一种使用多层神经网络求解高维向后微分方程的算法[9].2019年,He和Xu讨论了卷积神经网络与多重网格之间的关系[10].本文所采用的神经网络算法将常微分方程的残差及初边值条件残差之和作为损失函数,通过最小化损失函数求解和评估模型来训练神经网络中的权重,从而得出需要点的近似解.基于python语言,Adam优化器来解决离散优化问题.
1 预备知识
1943年,Mcculloch,Pitts将生物神经元模型抽象为图1所示的人工神经元模型[11].设神经元的输入为x1,x2,…,xn,这些输入通过带有权值w1,w2,…,wn的连接来进行传递, 然后通过加权求和得到总输入,再与神经元的阈值b作出比较,最后利用激活函数σ进行非线性变化得到神经元的输出y.人工神经元结构模型如图1所示:

图1 人工神经元的结构模型Fig.1 Structural Model of Artificial Neuron
上述神经元工作过程的数学模型如下:
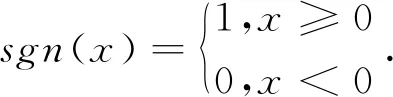

图2(a) 阶跃函数图像Fig.2(a) Graph of Step Function图2(b) Sigmoid函数图像Fig.2(b) Graph of Sigmoid Function
阶跃函数将神经元的输入映射为0或1,分别代表神经元的“抑制”与“兴奋”两种状态.但是,由于阶跃函数在阶跃点处的不连续和不可导,实际应用中常常采用图2(b)所示的Sigmoid函数:
Sigmoid作为激活函数,它能将神经元的输入值连续的映射到(0,1)范围内,并且能够进行多次求导,符合概率分布的特点.
2 单隐层神经网络的网络结构与BP算法

图3 单隐层神经网络结构Fig.3 Network Structure of Single Hidden Layer Neuron

神经网络的学习算法有很多,针对本文的单隐层神经网络问题,最常用的就是BP算法,(即误差反向传播算法)[12].BP算法由信号的正向传播与误差的反向传播两个部分组成.信号的正向传播即输入值通过输入层进入神经网络,经过隐藏层逐步传递至输出层,如果输出值跟期望值不符,则进入误差的反向传播过程;如果输出值跟期望值相符,则结束学习算法.误差的反向传播即将误差信号(输出值与期望值之差)按原来的连接反传计算,经过隐藏层最终达到输入层,在反向传播的过程中将误差分摊给每层的每个单元,得到每层每个单元的误差信号,并且将其作为修正每个单元权重的依据.这个过程一般采用梯度下降法[13]来完成,在不停修正各神经元的权值跟阈值的过程中,误差信号逐渐减小.




图4 节点j到输出层的信号流图Fig.4 Signal Flow Diagram of Node j to Output Layer
则e(n)对Wm+j(n)的梯度为:
根据梯度下降法可知,权值Wm+j(n)的改变量为:
其中,η为学习率. 第n次迭代结束后,输出层权值Wm+j(n)调整为:
Wm+j(n+1)=Wm+j(n)+ΔWm+j(n).


从而可得e(n)对Wj(n)的梯度为:
则e(n)对bj(n)的梯度为:
根据梯度下降法可知,权值Wj和阈值bj的改变量分别为:
其中,η为学习率. 第n次迭代结束后,输出层权值Wj和阈值bj分别调整为:
Wj(n+1)=Wj(n)+ΔWj(n),bj(n+1)=bj(n)+Δbj(n).

图5 输出层经过节点j到输出层的信号流图Fig.5 Signal Flow Diagram of the Output Layer Passing Through the Node j to the Output
3 神经网络求解常微分方程的算法思路
在实际问题中,期望值或真实值往往未告知,对于人工神经网络误差e的定义需要作出相应的调整.一般的n阶常微分方程具有形式

考虑如下的常微分方程初边值问题:求解y,满足
定义损失函数Loss为

4 网络推演过程及python程序


图6 第n次推演过程图Fig.6 Diagram of the nth Derivation
采用python语言求解常微分方程的近似解,其优点是处理大数据更加方便快捷,运行速度较快.程序编写可采用以下五个步骤实现:
(1)以包含边值条件的损失函数Loss满足收敛精度要求或给定迭代次数为停机条件,随机选取初始权值和阈值;


y1 = tf.nn.sigmoid(tf.matmul(x1, W)+b) W1 = tf.Variable(tf.zeros([g, 1]))y = tf.matmul(y1, W1)
(3)以损失函数是否满足停机条件来判断神经网络权值和阈值的更新;若不满足,则通过反向传播依次更新权值和阈值;

train_step = tf.train.AdamOptimizer(1e-2).minimize(Loss) init = tf.global_variables_initializer()sess = tf.InteractiveSession()sess.run(init)for i in range(50000): sess.run(train_step, feed_dict={x1: x_t}) if i % 50 == 0: total_Loss = sess.run(Loss, feed_dict={x1: x_t}) print("Loss={}".format(total_Loss)) print(sess.run(y[0], feed_dict={x1: x_t}))
(4)经过一次反向传播,更新权值和阈值,然后继续重复第(2)~(3)步;
(5)最终得出满足停机条件的神经网络.
4 数值算例


表1 几种方法对应的计算结果Tab.1 The Corresponding Results of Several Methods


表2 几种方法的计算结果Tab.2 The Results of Several Methods
通过数值算例,本文介绍的单隐层神经网络解法对于常微分方程问题的计算结果与改进欧拉方法,Heun's方法和文献[3]中方法相比,计算精度更高,误差更小.并且误差可以通过增加隐层神经元的个数或层数,或者使用遗传算法优化权重等方法去缩小,因此常微分方程可用神经网络求解.
5 结语
本文讨论了一种单隐层神经网络算法在数值常微分方程求解中的应用.文中将微分方程的求解问题与损失函数的优化问题联系起来,以损失函数的优化问题去训练神经网络进而得出微分方程的近似解,并通过网络推演观察到神经网络权值跟阈值的变化情况,最后使用python语言求解的数值算例证明了神经网络算法的精确性和实用性.

